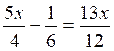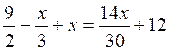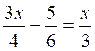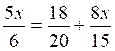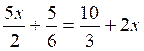|
|
|
DOC : Formation Individualisée |
DOC : Elève. |
|
ALGEBRE. N° 9 |
Information « TRAVAUX »
|
|
OBJECTIFS :-
médiation en algèbre. |
I )
Pré requis:
|
i9 |
Le calcul numérique |
:i |
|
i9 |
Liste des objectifs
« passerelle » 3ème / Seconde. |
:i |
|
i9 |
:i |
II )
ENVIRONNEMENT du dossier :
|
Info : |
Equation contenant des
fractions de « x » et des fractions de termes connus.
IV) INFORMATIONS
« formation leçon » :
|
Travaux auto - formation. |
|
Corrigé des travaux auto - formation. |
||||
|
Corrigé |
||||||
V ) DEVOIRS ( écrits):
|
Devoir diagnostique L tests. |
|
|
Devoir
Auto - formatif (intégré
au cours) |
|
|
Devoir Formatif « Contrôle :
savoir » ; (remédiation) |
|
|
|
|
|
Devoir sommatif. |
|
|
Devoir certificatif : (remédiation) |
|
* remédiation :
ces documents peuvent être réutilisés ( tout ou
partie) pour conclure une formation .
|
Leçon |
Titre |
|
N°9 |
Equation contenant des fractions de
« x » et des fractions de termes connus. |
I -Principes :
1°)
soit l’égalité 2 douzaines = 24
Multiplions les deux membres par
« 3 », on a 6 douzaines = 72
On obtient une nouvelle égalité.
Quand on multiplie les deux membres
d’une égalité (ou qu’on les divise) par un même nombre, on obtient une nouvelle
égalité.
2°) Soit la somme : 4 + 5 = 9
Multiplions les deux termes du premier
membre par 2, ils deviennent « 8 » et « 10 ».Si on les
additionnent « 8+10 » on obtient « 18 »
Or
« 18 » vaut deux fois le total de la première somme.(2 fois 9).
II) Résolution de l’équation : 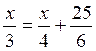
a)
Il
faut réduire toutes les fractions
au même dénominateur.
Le dénominateur commun pourrait
être de
3 fois 4 fois 6 soit : 72 ;
Mais il est remarquable que 3 fois 4
est égal à 4 fois 3 qui est égal à 2 fois 6
soit 12.
Le dénominateur commun sera
« 12 »
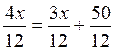
b)
on
multiplie les deux termes du second membre par « 12 »
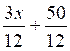 Devient
Devient 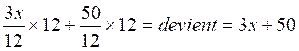
c)
Pour
rétablir « l’équilibre », il faut multiplier le premier membre par « 12 » également. 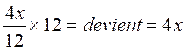
De l’équation (1) 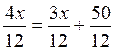 on obtient la
nouvelle équation (2) 4x = 3x + 50
on obtient la
nouvelle équation (2) 4x = 3x + 50
Tout ce passe comme si nous avions
supprimé les dénominateurs de l’équation de départ (1).
d) résolution : 4x = 3x + 50
Isolons « x » : 4x - 3x = 50
Soit : x = 50
Ce qu’il faut vérifier, en remplaçant
la valeur de « x = 50 » dans l’équation 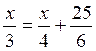
Soit
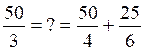
On retiendra :
Quand les « x » et les termes
connus sont sous formes fractionnaires, on réduit tous les termes au même dénominateur , puis on supprime ce dénominateur .Il reste a
calculer « x ».
|
Titre |
|
|
N°9 |
TRAVAUX d’Auto -
FORMATION sur Equations contenant des fractions
de « x » et des fractions de termes connus . |
Dans
une équation qui comprend des fractions de « x » entiers et des
fractions de termes connus que faut-il faire résoudre cette équation?
Exercices :
Résoudre les équations suivantes :
|
I)
|
|
|
·
a |
|
|
II)
|
|
·
b |
|
|
|
III)
|
|
·
c |
|
Pb 1:
Les 2/3 d’un nombre surpassent de 41 /
15 ses 3 /5 . Quel est ce nombre ?
Pb N°2 :
Deux ouvriers s’associent pour acheter une machine. La somme que possède le
premier suffit à en payer les 2/3 . Celle que possède
le second , les 3/7 . A eux deux ,
ils ont une somme qui dépasse de 150 € le prix de la machine. Quel est ce
prix ?
CORRIGE :
Exercices :
Résoudre les équations suivantes :
|
1 |
|
|
·
a |
|
|
2 |
|
·
b |
|
|
|
3 |
|
·
c |
|
Pb 1:
Les 2/3 d’un nombre surpassent de 41 /
15 ses 3 /5 . Quel est ce nombre ?
Pb
N°2 : Deux ouvriers s’associent pour acheter une machine. La somme que
possède le premier suffit à en payer les 2/3 . Celle
que possède le second, les 3/7. A eux deux , ils ont
une somme qui dépasse de 150 € le prix de la machine. Quel est ce prix ?