|
|
|
|
EXERCICES :
|
 s’écrit aussi : s’écrit aussi :
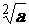
|
|
|
|
|
|
|
|
|
|
1.
|
Calculer :
|
corrigé
|
|
a
|
 = =
|
On a la forme
générale : ( a + b) ² = a + 2 ab + b²
|
|
b
|
 = =
|
On a la forme
générale : ( a - b) ² = a - 2 ab + b²
|
|
2.
|
Calculer :
|
|
|
a
|
 = =
|
Ecriture équivalente :
|
|
b
|
 = =
|
|
|
|
|
|
|
3.
|
Calculer :
|
|
|
a
|
 = =
|
|
|
b
|
 = =
|
|
|
|
|
|
|
4.
|
|
|
|
a
|

|
|
|
b
|
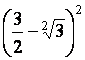
|
|
|
|
|
|
|
5.
|
Donner (Calcul) les inverses des nombres donnés,
on les écrira sous la forme « a + b » , « a » et « b » étant des
rationnels et « c » un entier « non- carré » » , « a » et « b » étant des
rationnels et « c » un entier « non- carré »
|
|
|
a
|
1 +  = =
|
|
|
b
|
 - 1 = - 1 =
|
|
|
|
|
|
|
|
|
|
|
6.
|
Calculer les inverses
des nombres donnés, on les écrira sous la forme « a + b » , « a » et « b » étant des
rationnels et « c » un entier « non- carré » » , « a » et « b » étant des
rationnels et « c » un entier « non- carré »
|
|
|
a
|
2 +  = =
|
|
|
b
|
 - 3 = - 3 =
|
|
|
|
|
|
|
7.
|
Calculer les inverses
des nombres donnés, on les écrira sous la forme « a + b » , « a » et « b » étant des
rationnels et « c » un entier « non- carré ». » , « a » et « b » étant des
rationnels et « c » un entier « non- carré ».
|
|
|
a
|
4 +  = =
|
|
|
b
|
3 - 2 = =
|
|
|
|
|
|
|
8.
|
Calculer les inverses
des nombres donnés, on les écrira sous la forme « a + b » , « a » et « b » étant des
rationnels et « c » un entier « non- carré ». » , « a » et « b » étant des
rationnels et « c » un entier « non- carré ».
|
|
|
a
|
3 +  = =
|
|
|
b
|
7 – 5  = =
|
|
|
|
|
|
|
9.
|
Calculer les inverses
des nombres donnés, on les écrira sous la forme « a + b » , « a » et « b » étant des
rationnels et « c » un entier « non- carré ». » , « a » et « b » étant des
rationnels et « c » un entier « non- carré ».
|
|
|
a
|
5 – 2 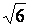 = =
|
|
|
b
|
5 + 2 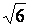 = =
|
|
|
|
|
|
|
10.
|
Comparer les valeurs numériques (nombres) suivants :
|
|
|
|
 et 2 + et 2 + 
|
|
|
|
|
|
|
11.
|
Comparer les valeurs numériques (nombres) suivants :
|
|
|
|
 et 2 + et 2 + 
|
|
|
|
|
|
|
|
|
|
|
12.
|
Comparer les valeurs numériques (nombres) suivants :
|
|
|
|
 + +  et 3 et 3
|
|
|
|
|
|
|
|
|
|
|
13.
|
Comparer les valeurs numériques (nombres) suivants :
|
|
|
|
 et et  + + 
|
|
|
|
|
|
|
|
|
|
|
14.
|
Comparer les valeurs numériques (nombres) suivants :
|
|
|
|
 et et 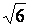 + + 
|
|
|
|
|
|
|
15.
|
Comparer les valeurs numériques (nombres) suivants :
|
|
|
|
1 -  et et  - - 
|
|
|
|
|
|
|
16.
|
Rendre rationnels les dénominateurs des valeurs (nombres) suivants :
|
|
|
a
|
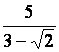
|
|
|
b
|

|
|
|
|
|
|
|
17.
|
Rendre rationnels les dénominateurs des valeurs (nombres) suivants :
|
|
|
a
|

|
|
|
b
|
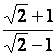
|
|
|
|
|
|
|
18.
|
Rendre rationnels les dénominateurs des valeurs (nombres) suivants :
|
|
|
a
|

|
|
|
b
|

|
|
|
|
|
|
|
19.
|
Rendre rationnels les dénominateurs des valeurs (nombres) suivants :
|
|
|
a
|
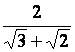
|
|
|
b
|

|
|
|
|
|
|
20.
|
Rendre rationnels les dénominateurs des valeurs (nombres) suivants :
|
|
|
a
|

|
|
|
b
|

|
|
|
|
|
|
|
21.
|
Rendre rationnel le dénominateur la valeur (nombres) suivant :
|
|
|
|
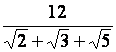
|
|
|
22.
|
Rendre rationnel le dénominateur la valeur (nombres) suivant :
|
|
|
|

|
|
|
23.
|
Rendre rationnel le dénominateur la valeur (nombres) suivant :
|
|
|
|
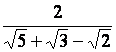
|
|
|
24.
|
Rendre rationnel le dénominateur la valeur (nombres) suivant :
|
|
|
|
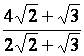
|
|
|
25.
|
Calculer 
|
|
|
|
En
déduire : 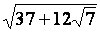 + + 
|
|
|
26.
|
Exprimer à l’aide d’un
dénominateur rationnel le nombre :
|
|
|
|
|
|
|
|
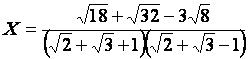
|
|
|
27.
|
Exprimer à l’aide d’un
dénominateur rationnel le nombre :
|
|
|
|

|
|
|
|
|
|
|
28.
|
On donne deux réels « p »
et « q » tels que 4 p3 + 27 q ²  0 0
|
|
|
|
|
|
|
|
On pose alors :
|
|
|
|
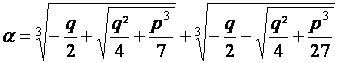 ; ;
Calculer le réel :  3+ p 3+ p 
|
|
|
|
|
|