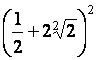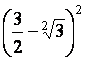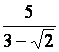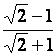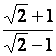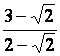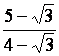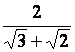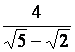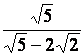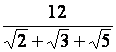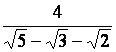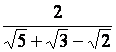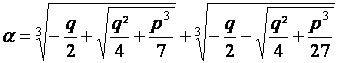|
|
Rappels de
cours :
|
|
>> Correction
|
|
|
|
|
|
|
|
« A » étant un réel positif , il existe deux
réels « a » et « a’ » dont le carré est égal à « A » .
Ils sont opposés. Celui des deux qui est positif se note «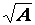 » et l’autre est «- » et l’autre est «-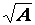 » . » .
« A » est appelé « le radicande »
|
|
|
|
Attention , il ne faut pas confondre :
|
|
|
|
·
La condition « A 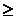 0 » indispensable pour que « A » soit un
radicande. 0 » indispensable pour que « A » soit un
radicande.
·
La convention selon laquelle 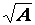 désigne un nombre
positif. désigne un nombre
positif.
|
|
|
|
|
|
|
|
« A » étant un réel quelconque, il existe un
réel unique « a » tel que
son cube soit égal à « A ». On note « 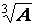 » . Les écritures « a3 » et « a = » . Les écritures « a3 » et « a = 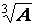 » ont exactement la même signification. » ont exactement la même signification.
|
|
|
|
Vous savez que les réels « r » tels que « r² » ne sont pas des
décimaux ; certes , on peut en donner des valeurs décimales approchées,
par exemple : « 1,414 » : mais les calculs ne
seraient alors approximatifs ; on trouverait pour « ( 1,41)4 » un peu
moins de « 3,952 » alors « r4 » est égal à
« 22 » , c'est-à-dire « 4 ».
|
|
|
|
On préfère souvent conduire tous les calculs
intermédiaires en conservant le signe
« 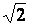 ,» et n’utiliser qu’à la fin , si cela est demandé, une
valeur approchée. ,» et n’utiliser qu’à la fin , si cela est demandé, une
valeur approchée.
|
|
|
|
|
|
|
|
Toutes les techniques de calculs ( à consulter ) dans un chapitre précédent
sont utiles , mais la formule fondamentale est :
a ² - b ² =
( a + b ) ( a - b)
|
|
|
|
En effet , si « a » ou « b » , ou les
deux, sont des radicaux ( sous entendu : portant sur des radicandes
entiers ou décimaux ) , « a² - b² » est entier ou décimal.
Des expressions telles que :
|
|
|
|
|
|
|
|
|
|
 et et 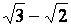
|
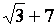 et et 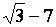
|
 et et 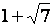
|
|
|
|
Sont
dites « conjuguées »
…
|
|
|
|
|
|
EXERCICES :
|
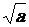 s’écrit
aussi : s’écrit
aussi : 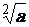
|
|
|
|
|
|
|
|
|
|
1.
|
Calculer :
|
|
|
a
|
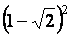 = =
|
|
|
b
|
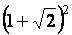 = =
|
|
|
2.
|
Calculer :
|
|
|
a
|
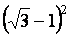 = =
|
|
|
b
|
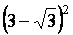 = =
|
|
|
|
|
|
|
3.
|
Calculer :
|
|
|
a
|
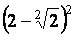 = =
|
|
|
b
|
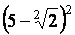 = =
|
|
|
|
|
|
|
4.
|
|
|
|
a
|
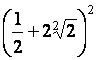
|
|
|
b
|
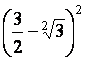
|
|
|
|
|
|
|
5.
|
Donner (Calcul) les inverses des nombres donnés,
on les écrira sous la forme « a + b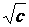 » , « a » et « b » étant des
rationnels et « c » un entier « non- carré » » , « a » et « b » étant des
rationnels et « c » un entier « non- carré »
|
|
|
a
|
1 + 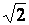 = =
|
|
|
b
|
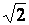 - 1 = - 1 =
|
|
|
|
|
|
|
|
|
|
|
6.
|
Calculer les inverses des
nombres donnés, on les écrira sous la forme « a + b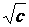 » , « a » et « b » étant des
rationnels et « c » un entier « non- carré » » , « a » et « b » étant des
rationnels et « c » un entier « non- carré »
|
|
|
a
|
2 + 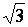 = =
|
|
|
b
|
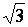 - 3 = - 3 =
|
|
|
|
|
|
|
7.
|
Calculer les inverses
des nombres donnés, on les écrira sous la forme « a + b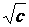 » , « a » et « b » étant des
rationnels et « c » un entier « non- carré ». » , « a » et « b » étant des
rationnels et « c » un entier « non- carré ».
|
|
|
a
|
4
+ 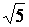 = =
|
|
|
b
|
3 - 2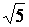 = =
|
|
|
|
|
|
|
8.
|
Calculer les inverses
des nombres donnés, on les écrira sous la forme « a + b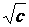 » , « a » et « b » étant des
rationnels et « c » un entier « non- carré ». » , « a » et « b » étant des
rationnels et « c » un entier « non- carré ».
|
|
|
a
|
3
+ 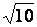 = =
|
|
|
b
|
7 – 5 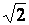 = =
|
|
|
|
|
|
|
9.
|
Calculer les inverses
des nombres donnés, on les écrira sous la forme « a + b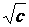 » , « a » et « b » étant des
rationnels et « c » un entier « non- carré ». » , « a » et « b » étant des
rationnels et « c » un entier « non- carré ».
|
|
|
a
|
4
– 2 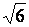 = =
|
|
|
b
|
5 + 2 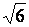 = =
|
|
|
|
|
|
|
10.
|
Comparer les
valeurs numériques (nombres) suivants :
|
|
|
|
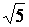 et 2 + et 2 + 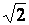
|
|
|
|
|
|
|
11.
|
Comparer les
valeurs numériques (nombres) suivants :
|
|
|
|
 et 2 + et 2 + 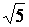
|
|
|
|
|
|
|
|
|
|
|
12.
|
Comparer les
valeurs numériques (nombres) suivants :
|
|
|
|
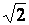 + +  et 3 et 3
|
|
|
|
|
|
|
|
|
|
|
13.
|
Comparer les
valeurs numériques (nombres) suivants :
|
|
|
|
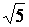 et et 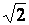 + + 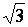
|
|
|
|
|
|
|
|
|
|
|
14.
|
Comparer les
valeurs numériques (nombres) suivants :
|
|
|
|
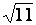 et et 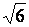 + + 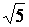
|
|
|
|
|
|
|
15.
|
Comparer les
valeurs numériques (nombres) suivants :
|
|
|
|
1 - 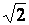 et et 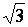 - - 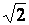
|
|
|
|
|
|
|
16.
|
Rendre rationnels les dénominateurs des valeurs (nombres) suivants :
|
|
|
a
|
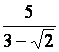
|
|
|
b
|

|
|
|
|
|
|
|
17.
|
Rendre rationnels les dénominateurs des valeurs (nombres) suivants :
|
|
|
a
|
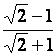
|
|
|
b
|
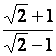
|
|
|
|
|
|
|
18.
|
Rendre rationnels les dénominateurs des valeurs (nombres) suivants :
|
|
|
a
|
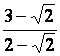
|
|
|
b
|
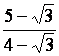
|
|
|
|
|
19.
|
Rendre rationnels les dénominateurs des valeurs (nombres) suivants :
|
|
|
a
|
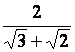
|
|
b
|
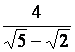
|
|
|
|
|
20.
|
Rendre rationnels les dénominateurs des valeurs (nombres) suivants :
|
|
|
a
|

|
|
|
b
|
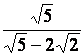
|
|
|
|
|
|
|
21.
|
Rendre rationnel le dénominateur la valeur (nombres) suivant :
|
|
|
|
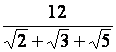
|
|
|
22.
|
Rendre rationnel le dénominateur la valeur (nombres) suivant :
|
|
|
|
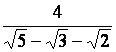
|
|
|
23.
|
Rendre rationnel le dénominateur la valeur (nombres) suivant :
|
|
|
|
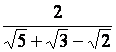
|
|
|
24.
|
Rendre rationnel le dénominateur la valeur (nombres) suivant :
|
|
|
|

|
|
|
25.
|
Calculer 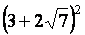
|
|
|
|
En
déduire : 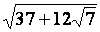 + + 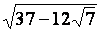
|
|
|
26.
|
Exprimer à l’aide d’un
dénominateur rationnel le nombre :
|
|
|
|
|
|
|
|
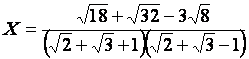
|
|
|
27.
|
Exprimer à l’aide d’un
dénominateur rationnel le nombre :
|
|
|
|
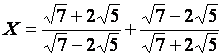
|
|
|
|
|
|
|
28.
|
On donne deux réels
« p » et « q » tels que 4 p3 + 27 q ² 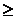 0 0
|
|
|
|
|
|
|
|
On pose alors :
|
|
|
|
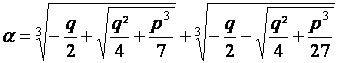 ; Calculer le
réel : ; Calculer le
réel : 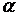 3+ p 3+ p 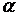
|
|
|
|
|
|
|
|
|
|