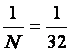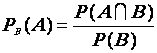|
|
|||||||||||
|
|
|||||||||||
|
|
|||||||||||
|
|
|||||||||||
|
ENVIRONNEMENT du dossier: |
|||||||||||
|
Objectif précédent : |
Objectif suivant : |
1°) Info liste des cours disponibles. . |
|||||||||
|
DOSSIER : PROBABILITES de base. Vocabulaire – définitions . ( cas particulier : situation d’équiprobabilité) LANGAGE
dit « ensembliste » et « probabiliste ». Probabilité : Notion de probabilité d’un
événement. Echantillon et notion de fluctuation
d’échantillonnage. |
|||||||||||
|
TEST |
COURS |
|
|||||||||
|
Vocabulaire : ·
« probabilité » :
caractère probable , vraisemblable ; ·
« calculs des probabilités »
: science visant à déterminer la vraisemblance d’un événement. Les probabilités sont une des
branches des statistiques. Dans « probabilité » il y
a le mot « probable » : ·
« Probable » : qui a
une apparence de vérité ;
signifie « peut être » ou « possible » ;
« cela peut arriver ……… » ; « il y a des chances, ou ,
une chance que … de se
produire.. » |
|||||||||||
Les probabilités sont souvent utilisées dans la vie courante comme étant l’étude des
« chances » de gagner à un jeu et par delà « gain
d’argent »..
Type de jeux : le « pile ou face » avec
une pièce , le jeu de dés ( avec 1 ou plusieurs) ; Le jeu de tirage de boules ( colorées , ou numérotés ) . Le loto …… ; la
loterie …… ; les courses (de chevaux
, de chiens ,………) ; les pronostiques…...
Rappel :
en
mathématique , pour noter un ensemble
on écrit une égalité : à gauche du signe égal on nomme l’ensemble par une lettre majuscule , à
droite du signe égal on écrit des accolades entre lesquelles on représente les
éléments qui composent cet ensemble . :
Exemple : ![]()
Si l’on veut
lister les 6 nombres d’un dé ; on nommera par A le dé et l’on écrira les 6 nombres dans des
accolades. Soit ![]() ou
ou ![]() ou
ou ![]() ou
……l’ordre des nombres n’est pas obligatoire…. ( voir des
exemples : @ les ensembles de nombres ..)
ou
……l’ordre des nombres n’est pas obligatoire…. ( voir des
exemples : @ les ensembles de nombres ..)
COURS
|
|
1.
« Expérience aléatoire » : Une
expérience dont les résultats dépendent du hasard est dit « expérience aléatoire » C’est
une expérience dont il est possible d’en connaître l’ issue sans avoir la certitude qu’elle se
réalisera. On
appelle « issue » la conclusion d’une expérience .. ;Il
peut y avoir plusieurs issues ,d’où plusieurs conclusions , ou
« éventualités » |
Exemple 1 : On
tire une carte dans un jeu de 32 cartes. |
Exemple 2 On
jette un dé. |
|
2. « événement » l’ensemble
des issues (éventualités) d’une expérience
compose « l’événement ». (on parle de « faisabilité » ,
l’issue est une possibilité ) On
compétera en disant que l’événement composé de toutes les issues ( notées : N ou « n » )
possibles est appelé « événement certain » Sa
probabilité vaut la valeur « 1 » |
|
Dans
un dé : N ou
« n » = 6 |
|
Par
exemple : soit l’expérience aléatoire
du jeté d’un dé à jouer. |
|
Il
y a 6 issues possibles |
|
Il
y a 6 issues possibles ; toutes les issues ( les 6 chiffres) possibles ont la même probabilité de sortir . On
dit que ces issues sont équiprobables
( même probabilité de sortir) ; on peut dire aussi que la
probabilité est équirépartie. Remarque :
la situation d’ équiprobabilité est un cas important : ( voir plus loin
) |
|
Les
6 issues possibles sont : les chiffres |
|
3. Lorsque l’on cherche à évaluer par calcul les chances de
réalisation d’un événement ; on dit que l’on évalue sa probabilité. Cette
probabilité est la somme des probabilités des issues qui la composent. |
|
|
|
4. « Evénement
élémentaire » : Un
résultat possible est un événement
élémentaire. Les
résultats possibles sont des événements élémentaires |
Dans
un jeu de trente deux cartes : Chaque
carte est un élément élémentaire . |
|
|
Et l’événement élémentaire a
pour probabilité |
La
probabilité de sortir (par exemple) le
roi de cœur est |
|
|
5. « Un événement
impossible » est un ensemble ( d’événements élémentaires) vide |
|
|
|
6. « L’ univers. » (Noté : ·
L’univers est l’ensemble
des résultats possibles ou
dit aussi : ·
L’univers est l’ensemble
des éventualités. |
L’univers
est la liste de toutes les cartes qui composent le jeu de cartes. |
L’univers
est la liste de tous les chiffres que contient le dé . |
|
Remarque : si l’ univers Explication : les nombres 1 ;
2 ; 3 ; 4 ; 5 ; 6
sont les nombres numérotant les
6 faces d’un dé Si
je jette le dé , j’aurai un des 6 nombres , si je parie sur les 6 nombres ,
je suis sûr de gagner ; on dit
que : l’événement est certain., |
||
(Voir : l’activité 1 .)
|
Activités 1 : |
|
||
|
Dans
un sachet on y met 3 haricots ( ensemble : H ) : un rouge
( R) ; un blanc ( B ) et un noir ( N) On plonge la main dans le sachet , on tire un haricot (au hasard)…et l’on
note sa couleur.
|
Faire
l’expérience avec plusieurs personnes , et noter les résultats.. |
||
|
|
|||
|
Inventaire des
Situations prédictives : (Noté : |
|
||
|
|
|||
|
Evénement
élémentaire : |
Notation : |
||
|
·
Tirer un haricot rouge |
|
||
|
·
Tirer un haricot blanc |
|
||
|
·
Tirer un haricot noir |
|
||
|
Mais
on peut aussi : |
|
||
|
·
Tirer un haricot qui n’est pas
rouge : |
|
||
|
·
Tirer un haricot qui n’est pas
noir : |
|
||
|
·
Tirer un haricot qui n’est pas
blanc : |
|
||
|
Et : |
|
||
|
·
Tirer un haricot
orange : |
|
||
|
·
Tirer un haricot qui n’est pas
vert : |
|
||
Bilan
de cette activité :
|
L’ensemble des résultats ( éventualités) dit « univers » est |
|
|
On
dénombre huit événements |
|
|
Les
événements qui comportent un seul élément ( singleton) sont aussi appelés
« événements élémentaires » |
Se
sont : |
Situation d’équiprobabilité :
|
Rappel
« n » ou « N » représente la somme des événements
possibles ( probable). La
situation est dite « d’
équiprobabilité » lorsque chaque événement élémentaire a pour
probabilité : C’est
le cas
où l’on a un choix au hasard
(tirer une carte ) ou lorsque l’on doit lancer un dé ( bien équilibré
, sinon possibilité de fraude) |
Dans
un dé : pour sortir un chiffre ;
N = 6 |
|
Si
on désigne par la lettre
« P » la probabilité , et par la lettre « A » un
événement quelconque ; dans une situation d’équiprobabilité on aura :
|
|
Langage élémentaire
« ensembliste » et « probabiliste » :
Commentaire :
comme pour les définitions qu’il faut s’approprier , le langage
probabiliste est à connaître …..
|
|
Cas d’un jet d’un dé : |
|
« L’ univers. » (Noté : |
|
|
L’événement
qui est une partie de l’univers est noté
A ; A Un
événement peut posséder 1 seul ou plusieurs éléments élémentaires. |
L’événement :
on demande la probabilité d’obtenir un chiffre pair : On
notera l’ événement : |
|
L’événement
impossible est appelé : « ensemble vide » ; utilisera la
lettre « phi » : On
dit aussi que : |
Ainsi :
obtenir le chiffre « 7 » sur un dé à 6 faces numéroté de 1 à 6 est
impossible. On
notera : |
|
L’événement
contraire de A est noté ( A barre) :
|
Ainsi
si l’ événement : |
|
|
|
|
Cas
où , il peut y avoir 2 événements possibles : A et B Rappel :
Un
événement peut posséder 1 seul ou plusieurs éléments élémentaires. |
|
|
Pour
noter qu’il y a réunion entre deux
événements , on sépare les deux lettres majuscules par un signe (u) :
; ( lire : ou ) La
réunion de l’événements A avec l’événement B sera noté A |
Notation
: A |
|
·
La réunion de ces deux événement est un événement qui contient
tous les événements élémentaires de A
ou de B . |
|
|
Pour
noter l’intersection de deux événements
, on sépare les deux lettres majuscules par le signe : |
|
|
·
L’intersection de l’ événement
A avec l’événement B , est notée : |
Notation : |
|
Lorsque les éléments sont
incompatibles on note : |
|
|
Activités 2 : |
|
|
On
jette un dé équilibré dont les facs sont numérotées de 1 à 6 ; on ne s’intéresse au numéro
apparaissant sur la face supérieure. |
|
|
Questions. |
Réponses : |
|
1°)
Quel est l’ensemble des éventualités (univers) |
|
|
|
Commentaire :
il y a autant d’événement que de parties de |
|
2°) Combien y a – t- il d’événements ? |
|
|
Il y a autant d’événements que de partie de |
Le nombre d’éléments est de 2 6 = 64 |
|
|
|
|
|
|
|
|
|
|
|
|
Probabilités
conditionnelles . Indépendance.
|
Définition
1 Soit
2 événement appelé A et B : La
probabilité que l’événement A se
réalise sachant que l’événement B est
réalisé est notée : PB ( A)
ou P ( A I B) et est définie
par : Remarque :
par transformation on a alors la
formule : P ( A |
|
Définition
2 On
dit que deux événements A et B sont
indépendants lorsque PB ( A) = P
( A) ou PA (B) = P (B) Remarque :
on obtient la formule : P ( A |
COMBINAISONS.
|
TRAVAUX
AUTO – FORMATIFS |
|
|
CONTROLE:
Série 1 : Questions sur le Vocabulaire :
Définitions .
|
Qu’est ce qu’une « Expérience
aléatoire » ? |
|
Qu’appelle – ton « issue » ? On
appelle « issue » la conclusion d’une expérience .. ;Il
peut y avoir plusieurs issues ,d’où plusieurs conclusion… |
|
Que compose
l’ « événement » ? l’ensemble
des issues d’une expérience compose
« l’événement ». Par quelle lettre désigne-t-on l’événement ? l’événement
composé de toutes les issues (
notées : N ou « n » ) possibles est appelé « événement
certain » Quelle est la valeur numérique de toutes les
issues d’un événement ? Sa probabilité
vaut la valeur « 1 » |
|
|
|
Quand
dit –on qu’iI y a situation d’ équiprobabilité Lorsqu’il y a 6 issues possibles ; et que toutes les issues ont la même probabilité de sortir on dit que ces issues sont équiprobables ( même probabilité de sortir) ; on
peut dire aussi que la probabilité est équirépartie.
on peut dire aussi que la probabilité est équirépartie. |
|
Compléter la phrase suivante : Lorsque
l’on cherche à évaluer par calcul les
chances de réalisation d’un événement ; on dit que l’on évalue
……………………………..sa probabilité. Cette probabilité est la somme des probabilités des issues qui la
composent. |
|
Qu’est ce qu’un « Evénement
élémentaire » ? : un événement élémentaire est
un résultat possible . Compléter la phrase suivante Les résultats possibles sont des événements élémentaires |
|
|
|
Que dit-on d’un « Un événement
impossible » : un événement impossible est
dit « ensemble ( d’événements élémentaires) vide ». |
|
|
|
Compléter la phrase : L’
univers est un événement certain. Qu’appelle-t-on « univers. » : on appelle « ’univers » l’ensemble
des résultats possibles . par
quelle lettre grecque le note t-on ? l’univers est Noté
par la lettre : |
|
|
Série
1 :
|
On
jette un dé dit équilibré , possédant 6 faces . |
|
Dans
un dé quelle est la valeur de N
ou « n » = 6 |
|
Combien
y a – t- il d’issues possibles ? Il y a 6 issues possibles |
|
Quelles
est le nom donné aux 6 issues
possibles sont : les chiffres |
|
|
|
Nommer
les 6 issues possibles : |
|
Ecrire
l’égalité mathématique de cette
situation d’équiprobabilité : |
|
|
|
|
|
Représenter
symboliquement l’univers est la liste
de tous les chiffres que contient le dé : . |