Prérequis:
|
Les problèmes proposés touchent tous les domaines mathématiques ;il faudra voir au cas par cas . |
ENVIRONNEMENT
du dossier:
|
Objectif suivant |
CORRIGE |
CORRIGE :
DOSSIER
: LES PROBLEMES DE
CONCOURS ! ! ! !
|
I ) Un négociant en vins réalise un bénéfice
de 30% sur le contenu d’un tonneau de
vin acheté 90 F.Il en vend 45litres et le prix de vente de la quantité
restante est de 27 F. Combien de litres le tonneau contenait-il à l’
achat ? 1- 54 litres 2-58,5 litres 3- 60 litres 4- 67,5 litres Réponse : bénéfice : 90 Prix de vente du total : PA + bénéfice
Soit 90 + 27 = 117 F Il a vendu pour 117 – 27 = 90
F les 45 litres Prix de vente d’un litre : 90 : 45 = 2 F /l Nombre de litres à vendre : 117 : 2 =
58 ,5 litres |
|
|||||||||||||||||||||||||||
|
Planète Gravitation Mercure 4 Terre 10 Uranus 11 Pluton 2 « u » étant la vitesse initiale de l’athlète ,
et « g » étant la valeur de la gravitation locale. Lors de l’appel pour sauter , le centre de gravité de
l’athlète est à 1 m de haut . Les gravitations des différentes planètes sont les
suivantes : Pour un athlète
courant à 5 m / s , laquelle des propositions suivantes est fausse : 1-l’athlète sautera plus haut sur la Terre que sur Uranus
. 2- l ‘ athlète sautera deux fois plus haut sur Pluton que sur Mercure . 3-Sur Mercure , le saut dépassera 4 m . 4 – Sur Terre , la hauteur du saut de l’ athlète est de
2,25 m Réponses : Saut sur Mercure : Saut sur Terre : Saut sur Uranus : Saut sur Pluton : Etude des propositions : 1-l’athlète sautera plus haut sur la Terre que
sur Uranus .(VRAIE) 2- l ‘ athlète sautera deux fois plus haut sur
Pluton que sur Mercure .(FAUSSE ) 3-Sur Mercure , le saut dépassera 4 m . .(VRAIE) 4 – Sur Terre , la hauteur du saut de l’ athlète
est de 2,25 m.(VRAIE) |
|
|||||||||||||||||||||||||||
|
III ) Deux
personnes se partagent à parts égales la somme de 24 000F.L’une place la
somme reçue à un taux de 12% par an , l’autre achète 30 actions qu’elle
revend au bout de six mois. Six mois après le partage , leur avoir total s’élève à 32
250 F. Quel est le gain réalisé sur chaque action vendue ? 1- 236 F. 2- 260 F. 3- 660 F. 4- 684 F. Résolution : Somme reçue : 24 000 : 2 = 12 000 F. Intérêt reçu au bout de six mois placé à 12
% : ( Avoir du premier : 12 000 + 720 = 12 720 F. Avoir du second : 32 520 – 12720 = 19 800
F. Gain réalisé par les 30 actions : 19 800 –
12 000 = 78 00 F. Gain réalisé par une action : 7 800 :
30 = 260 F. |
||||||||||||||||||||||||||||
|
IV ) La pointe de l’aiguille des
secondes d’une horloge , qui suit exactement le bord du cadran , parcourt 180
mètres en une heure. Quelle est , en m2 , la surface du
cadran ? 1- 0,75 m2 2- 3 m2 3- 7,5 m2 4- 30 m2 prendre : p = 3 Réponse : Le
tour de cadran se fait en 1 minute : D’où le
périmètre du cadran = 180 : 60 =
3 m Donc le rayon du cadran : * Périmètre du cadran circulaire : P = 2 pR donc 3 =
2 Surface du cadran : pR2 = 3 |
||||||||||||||||||||||||||||
|
V ) Une ville est constituée par 3 cercles concentriques de rayons
respectifs : 3 km , 10 km et 20 km . Le centre ville a une densité de
population de 20 000 habitants/km2 , la petite couronne 10 000
habitants/ km2 et la grande couronne 2 000 habitants/km2. Quelle est la population totale de la ville ? 1- 1 200 000
habitants 5- 1 800 000 habitants 6- 5 070 000 habitants. 7- 5 940 000 habitants . prendre : p = 3 REPONSE : Centre : aire du
centre : pR2 = 3fois 3
fois 3 fois population centre : 27 fois 20 000 = 540
000 h petite couronne aire de la petite couronne :
3 fois10 au carré moins 27 km2 = 273km2 population petite couronne : 273 foi 10000
= 2 730 000 h grande couronne aire : grande couronne : 3
fois 20 au carré moins 300 = 900 km2 population grande couronne : 900 fois 2000
= 1 800 000 h population totale : 540 000 h + 2
730 000 h + 1 800 000 h = 5 070
000 h. |
|
|||||||||||||||||||||||||||
|
1997 1998 présentés reçus présentés reçus Non-redoublants 22 12 15 8 Redoublants 3 3 10 9 Total 25 15 25 17 Parmi les affirmations suivantes , laquelle est
fausse ? 1- en 1997 :les non-redoublant représentent 4/5 des
reçus. 2-en 1998 : les redoublants représentent 2/5 des candidats
présentés. 3- en 1997 :20 % de redoublants parmi les reçus. 4- en 1998 : le nombre de redoublants reçus est en
augmentation de 200% par rapport à 1997 . Réponse : il faut prendre affirmation par affirmation : 1- en 1997 : 12 non redoublants sont reçus
sur 15 : mais Commentaire : on peut considérer que
les autres affirmations sont vraies ; nous devons le vérifier : 2-en 1998 : 10 redoublants
se sont présentés sur 25 :soit il faut rendre
irréductible donc : les redoublants représentent 2/5 des
candidats présentés. 3- en 1997 :20 % de
redoublants parmi les reçus. ? SOS COURS il y a 15 reçus : on calcule les 20% de 15
= on a bien 20% de redoublants reçus. ! 4- en 1998 : le nombre de redoublants reçus
est en augmentation de 200% par rapport à 1997 . il y a eut 9 redoublement reçus en 1998 contre 3
en 1997 soit une différence de + 6 . nous allons calculer les 200% de 3 : cette dernière affirmation est aussi
vraie ! CONCLUSION : la première affirmation est
fausse ! |
|
|||||||||||||||||||||||||||
|
1ère catégorie 70 fois 3= 210 dm3 2ème catégorie : 1l =1dm3 6 fois 30 dm3 180 dm3 3ème catégorie 20 cm3 =0,020 dm3 25 fois 0,020 0,5 dm3 Total : 390,5 dm3 Si on mélange 3 lots de plumes de 1ère
catégorie , 6 lots de 2ème catégorie et 25 lots de 3ème
catégorie , quel sera le volume de la couette obtenue ? 1-228,5 dm3 2- 390,5 dm3 3- 395 dm3 4- 440 dm3 Réponse : Conclusion : la solution 2 est la bonne. |
|
|||||||||||||||||||||||||||
|
VIII ) Quelle est la valeur d’un
nombre entier tel qu’en lui ajoutant 12 ou 25 , les deux sommes
respectivement obtenues soient des carrés parfaits ? 1- 11 2- 24 3- 52 4- 69 Réponse : 24 +12 = 36 est le carré parfait
de « 6 » 24 +25 = 49 ; 49 est le carré parfait de
« 7 » |
|
|||||||||||||||||||||||||||
|
IX ) Deux villes A et B sont distantes de 45 km. Un
cycliste part de A à la vitesse de 24 km /h ;un deuxième cycliste par de
B , 25 min après le départ du premier
et le croise après avoir par couru 15 km. Quelle est la vitesse du deuxième cycliste ? 1- 8km /h 2- 12 km/ h 3- 15 km /h 4- 18 km /h Réponse : Distance parcourue part le premier cycliste (SOS COURS) :au bout de 25 min (24 :60) 25=10 km ; il lui reste à
parcourir :45-10= 35 km au moment où le second par de B ; le premier à parcourue 35-15 = 20 km au moment où les deux cycliste
se sont croisés, ce qui représente en temps : (20 / 24)60 = 50
min) (SOS
COURS) le second parcours 15 km en 50 min ; sa
vitesse est (de 15/50)60=18 km /h |
|
|||||||||||||||||||||||||||
|
Prix Tarif rouge De 8h à 12 h 30 0,70 F par période
de 12 secondes Tarif blanc De 18 h à 21h 30 0,70 F par période
de 18 secondes Tarif bleu De 221 h30 à 22 h30 0,50 F par période
de 18secondes Une facture de téléphone comprend pour un bimestre : -
l’abonnement de 80 F -
le coût total des
communications. Monsieur François ne
téléphone qu’en période bleue. Combien de temps a-t-il
téléphoné sachant que sa facture s’élève à 430 F ? Propositions : -
1- 2h 20 min. -
2 – 2h 30 min -
3 – 3 h 30 min -
4 - 5 h 06 min . Réponse : coût total des
communications : 430-80 = 350 F Nombre de périodes (période bleue ) de 18 sec. : 350 : 0,5 =700 Durée des communications en secondes : 700
fois 18 =12 600 sec. Durée en heures , minutes secondes : 12600 : 3600 = 3,5 heures 0,5h = 30 min donc le temps de communication est
de 3 h 30 min. |
|
|||||||||||||||||||||||||||
|
XI ) Soit une droite D d’équation 2x
–3y +6 = 0 Parmi les proposition suivantes , laquelle est
fausse ? 1- D a pour vecteur directeur le
vecteur de coordonnées (3 ; 2 ) 2- D passe par le point de coordonnées ( -3 ; 0 ) 3- D a pour coefficient directeur 3 / 2 4- D a pour ordonnée à l’origine 2 D a pour vecteur
directeur le vecteur de coordonnées
(3 ; 2 ) : 3y = 2x + 6 soit y = les coordonnées du vecteur A B sont (xB-xA)
et (yB-yA) Soit A(0 ;2) et B (3 ;4 ) : ainsi
(xB-xA) =(3-0) = 3 et (yB-yA) = (4-2) = 2 les coordonnées du vecteur AB sont ( 3 ; 2
) D passe par le point de
coordonnées ( -3 ; 0 ) : Si x = -3 ; y= Proposition « 3 » : fausse ; D
n’ a pas pour coefficient directeur 3 / 2 mais 2/3
Proposition « 4 » : vraie ; Si « x » = 0 ; y = 2 ; (y = |
|
|||||||||||||||||||||||||||
|
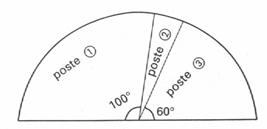
Poste 1 : chauffage (fuel) Poste 2 : eau , électricité. Poste 3 : entretien , syndic , concierge . Sachant que le montant total de ses charges s’élèves à 2
700 F, que le montant des charges dues au chauffage est proportionnel au
nombre de pièces alors que celui des autres charges est fixe , le montant
annuel des charges pour l’occupant d’un appartement de cinq pièces sera
de : 1- 2500F 2- 3500 F. 3- 3700F. 4- 4500F. Résolution : 180° représente sur le graphique 100% des
charges. Le poste 1 : (100 °) représente Le poste 2 : ( 180° - (100°+60°)) = 20
° ;représente Le poste 3 : (60°) représente : Les charges incompressibles sont dans le poste 2
et 3 (80°) : Soit Montant des charges incompressibles d’un
appartement : 2700 fois
( Montant des charges pour trois chambres :
2700 –1200 = 1500 F Montant des charges pour une chambre =
1500 : 3 = 500F Calcul du loyer pour cinq chambres : 1200F + 5 fois 500F = 1200 + 2 500 = 3 700F la proposition « 3 » est la
bonne ! ! |
|
|
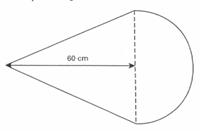
Quelle est la surface totale , en cm2 , du
cerf-volant ? 1- 1800 cm2 2- 2400 cm2 3- 3600 cm2 4- 6000 cm2 ( p = 3 ) résolution : 1 ) aire d’un triangle : nous
avons : 2)calcul du rayon : 40 :2 = 20 cm 3) Surface totale : égale la surface du
triangle plus l’aire du demi-cercle :
1200 + 3 (20 fois 20 ) / 2 = 1200 + 600 = 1800 cm2 la proposition « 1 » est la bonne . |
|
CONCOURS de surveillants
des services déconcentrés de l’administration pénitentiaire :
Conditions : 1 heure ; l’usage de la calculatrice
est interdite .
Tous les raisonnement calculs et opérations devront
apparaître clairement sur les copies.
|
I ) résoudre dans
« R » l’équation : ( 2x +3 ) (x –4 ) = ( 3x – 2 ) ( x + 6 ) résolution : a) Développons le premier membre : ( 2x +3 ) (x –4 ) = 2 x2 –8x + 3x –12 nous ordonnons (voir « factorisation pour regrouper – 8x + 3 x ) ( 2x +3 ) (x –4 ) = 2 x2 –5x –12 b ) Développons le second
membre : ( 3x – 2 ) ( x + 6 ) =
3 x2 +18x –2x -12 ( 3x – 2 ) ( x + 6 ) =
3 x2 +16x -12 c) ( 2x +3 ) (x – 4 ) = ( 3x – 2 ) ( x + 6 ) devient : 2 x2 – 5x –12 =
3 x2 +16x -12 nous obtenons : 3 x2 +16x -12 - 2 x2 + 5x +12 = 0 on ordonne : 3 x2 - 2 x2
+16x + 5x +12 -12 = 0 on réduit : x2 +21 x = 0 Nous avons une forme : a x2
+b x = 0 , ce qui
donne en factorisant x ( ax +b) =0 L’équation à deux solutions : (
le produit est égal à 0
si un des produit est nul
) Ainsi : x (x +21) = 0
On en déduit une première solution (racine) x = 0
La deuxième solution est
obtenue en posant
x +21 = 0 ; Cà d x = -21 |
|
II ) On considère l’équation f(x) de R dans R définie par : F(x) = 5 x2 – 4x + 9 A) calculer f pour x = 5 B) calculer f pour x = -1 Résolution : A ) F(x) = 5 x2 –4x + 9 ;
F(5) = 5fois 52 –
4fois 5 + 9 =125 –20 + 9 = 114 B) F(x) = 5 x2 – 4x +9
F(-1) = 5fois (-1)2
– 4fois -1 + 9 = 5 + 4 + 9
= 18 |
|
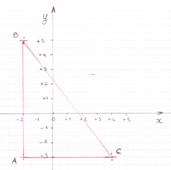
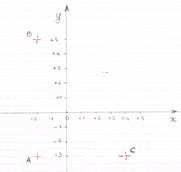
On place les points
A ( -2 ;-3 ) , B ( -2 ;5 ) et C ( 4 ;-3) a) montrez que le triangle
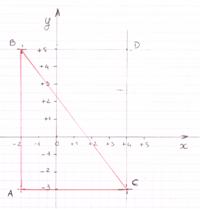
ABC est rectangle b) Calculez les coordonnées du milieu M du segment [AB] Résolution : Il faut placer les points dans un repère : Il faut repérer l’hypoténuse du triangle qui serait
rectangle .
L’hypoténuse « pourrait être » le segment de droite BC Si BC2 = BA2 + AC2 , on en conclura que le triangle ABC est
rectangle . Calcul de la mesure
du segment AB : ½yB - yA ½= ½ ½(+5) - (-3) ½= ½+8½
= 8 Calcul de la mesure du segment AC : ½xC - xA ½= ½
½(+ 4) - ( - 2) ½= ½+ 6½ = 6 Commentaires : a ) le segment AB est parallèle
à l’axe « y » (les extrémités ont la même ordonnée ) b) le segment
AC est parallèle à l’axe « x » (les extrémités ont
la même abscisse) donc : les
deux segments sont donc perpendiculaires
Calcul de la mesure
du segment BC : Il reste à
montrer par le calcul que BC est l’hypoténuse du triangle rectangle
en calculant la somme des carrés des cotés (représentés par
les projetées BD et DC) Calcul de
« BC » si «AC »
= 6 et « AB » = 8 BC2 =
AB2 + AC2
On pose
de l’égalité on en
tire que : le premier membre on conclut que la distance entre BC =
10 |
Autre concours :
|
PROBLEME On donne : en 1998 il y a en France 60 000 000 de personnes . En quelle année la
population aura-t-elle doublée (120 000 000 de personnes ) sachant que sa
croissance annuelle est de 3% |
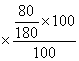 =1200 F.
=1200 F.