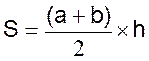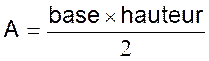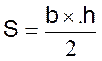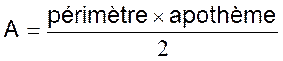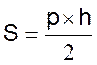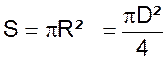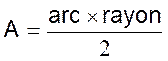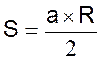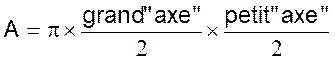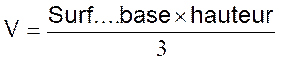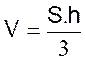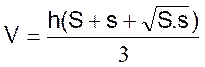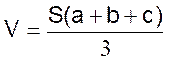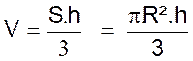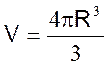|
DOSSIER N° index warmaths . |
Matière : MATH - SCIENCES |
|
|||||||||
|
|
|
||||||||||
|
FORMULAIRE : AIRE et VOLUMES |
|||||||||||
|
|
|||||||||||
|
OBJECTIFS :- Savoir les formules
des aires et volumes |
|||||||||||
|
|
I )
Pré requis: (pour remédiation ou mise à niveau) |
|
|
|||||||
|
|
|
|
|
|||||||
|
i9 |
:i |
|
||||||||
|
|
|
|
|
|||||||
|
i9 |
:i |
|
||||||||
|
|
|
|
|
|||||||
|
|
|
|
||||||||
|
|
|
||||||||||
|
I ) LES
CACULS D’ AIRES |
|
|
Définition |
Figure |
Aire |
|
Rectangle : quadrilatère dont les quatre angles sont droits. |
|
A = longueur ´ largeur Ou S = = a b |
|
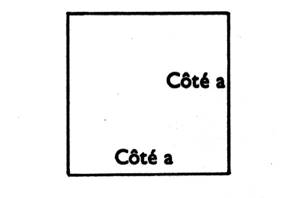
Carré : Est un rectangle dont les côtés sont égaux |
|
A = côté ´ côté Ou S = = a a
ou S = a² |
|
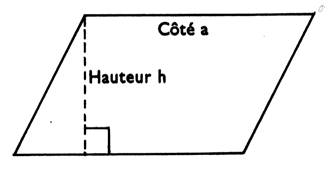
Parallélogramme : Quadrilatère dont les côtés opposés sont parallèles. |
|
A = côté ´ hauteur abaissée sur ce côté. S = a . h |
|
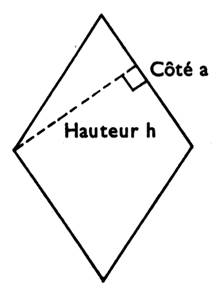
Losange : parallélogramme dont deux côtés consécutifs sont égaux. |
|
A = côté ´ hauteur S = a . h |
|
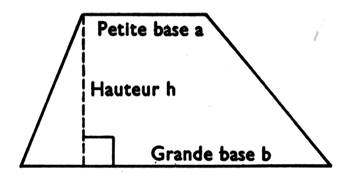
Trapèze : Quadrilatère dont deux côtés opposés sont parallèles. |
|
A= demi somme des bases´ hauteur Ou
|
|
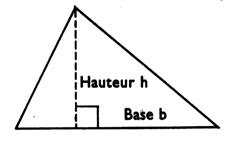
Triangle : figure à trois côtés. |
|
ou
|
|
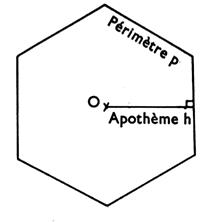
Polygones réguliers : figure dont les côtés ainsi que les angles
au sommet sont égaux. |
|
ou
|
|
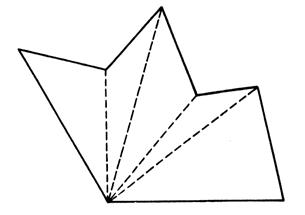
Polygone irrégulier : figure formée par une ligne brisée fermée
alternant le concave et le convexe. |
|
Il faut diviser la surface en autant de triangles qu’il est
nécessaire, et faire la somme de ces surafces. |
|
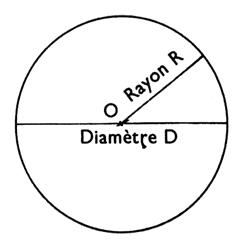
Cercle : figure formée par une ligne plane fermée dont tous les
points sont à égale distance d’un point de son plan, appelé « centre ». |
|
A = p ´ rayon ´ rayon. Ou
|
|
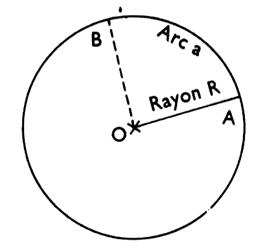
Secteur circulaire : portion de cercle comprise entre un arc AB
et les rayons OA et OB. |
|
ou
|
|
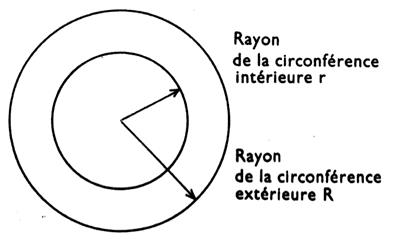
Couronne circulaire : portion de surface comprise entre deux
cercles concentriques. |
|
A= p ´ différence des carrés des rayons Ou S = p ( R² - r² ) |
|
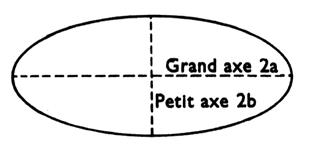
Ellipse : courbe plane telle que la somme des distances de chacun
de ses points à deux points fixes déterminés de son plan (
les foyers) soit constante. |
|
ou
|
|
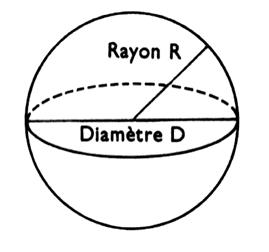
Sphère : solide dont tous les points de la surface sont à égale
distance d’un point intérieur appelé « centre ». |
|
ou
|
|
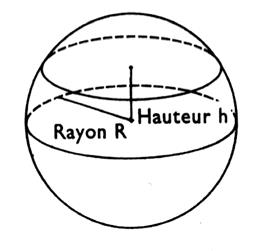
Zone de sphère : portion de la surface d’une sphère comprise
entre deux plans parallèles. |
|
A= 2 p´ rayon de la sphère ´ hauteur de la zone. Ou
|
|
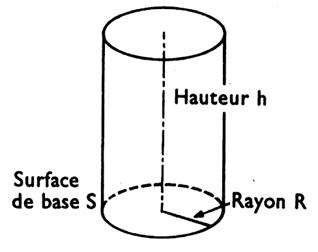
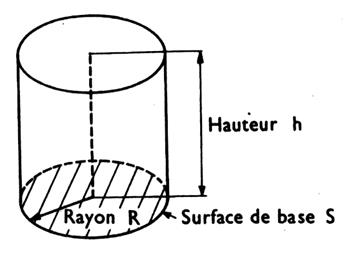
Cylindre circulaire droit : solide engendré par la révolution
d’un rectangle tournant autour d’un de ses côtés. |
|
Surface latérale : longueur de la circonférence de la base ´hauteur. A lat .= 2 p R h Surface totale : A lat + A bases. Stot.= 2 p R h + 2 p R² |
|
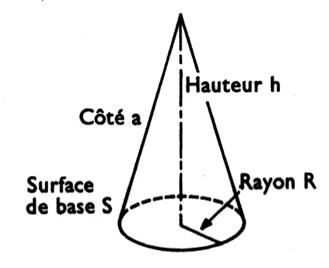
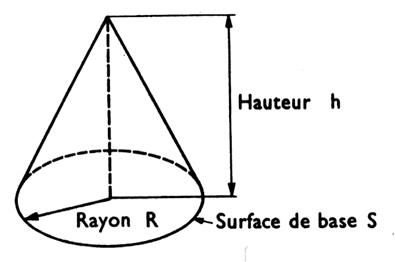
Cône circulaire droit : solide engendré par la révolution d’un
triangle tournant autour d’un des côtés de l’angle droit. |
|
Surface latérale : 1/2 ´ longueur de la
circonférence de la base ´ côté. S = p R a |
|
LES CALCULS DE
VOLUMES |
|
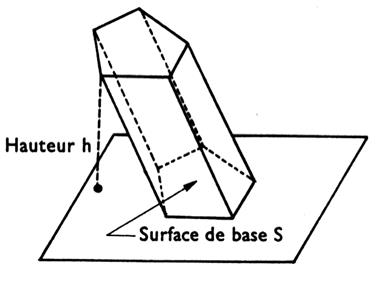
Prisme : figure limitée de tous côtés par des
polygones tels que les faces latérales soient des parallélogrammes et que les
bases soient deux polygones plans
égaux et parallèles. |
|
V = surface de base ´
hauteur. Ou V = S . h |
|
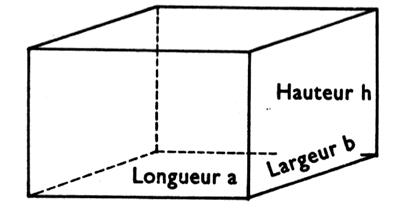
Parallélépipède rectangle : prisme droit dont les bases sont des
rectangles. |
|
V=
longueur ´ largeur´ hauteur. V
= a . b . h |
|
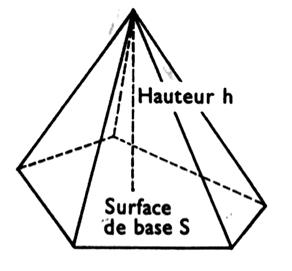
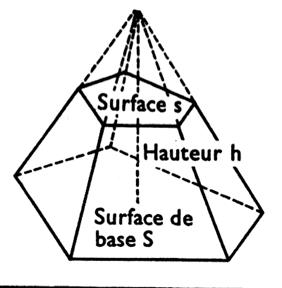
Pyramide : solide dont une face (base) est un
polygone plan et dont les faces latérales sont des triangles ayant pour bases
respectives les côtés de ce polygone et pour sommet commun un point extérieur
au plan du polygone. |
|
ou
|
|
Tronc de
pyramide à bases
parallèles :
solide
obtenu en coupant une pyramide par un plan parallèle à la base et en enlevant
la partie supérieure. |
|
V = la somme des volumes de trois
pyramides de même hauteur et dont les bases
auraient des aires respectivement
égales à
S ; s ;
|
|
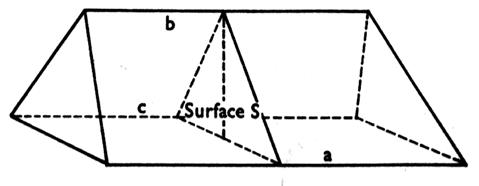
Tronc de prisme triangulaire : solide obtenu en tronquant un prisme
triangulaire par un plan non parallèle aux bases et en enlevant une des deux
parties.
|
|
V = Surface d’une section droite ´ le tiers de la somme des trois
arêtes latérales.
|
|
Cylindre |
|
V = surface de base´hauteur V
= S . h
= p R² h |
|
Cône circulaire droit. |
|
V = 1/3 ( surface
de base ´
hauteur)
|
|
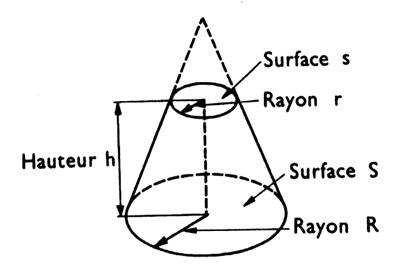
Tronc de cône à bases
parallèles : solide
obtenu en coupant un cône par un plan parallèle à la base et en enlevant le
cône supérieur.: |
|
V = la somme des volumes de trois cônes de même hauteur
et dont les bases auraient des aires
respectivement égales à S ;
s ;
ou
|
|
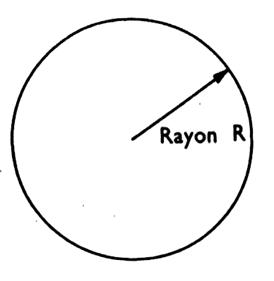
Boule |
|
ou
|
|
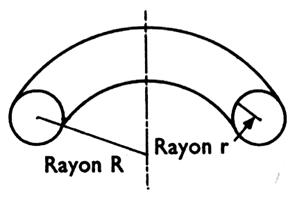
Tore : solide engendré par la
rotation d’un cercle autour d’un axe situé dans son plan mais extérieur à ce
cercle. |
|
V = aire de la section ´
longueur d la circonférence moyenne V = p
r² ´2
p
R = 2p²
r² R |
|
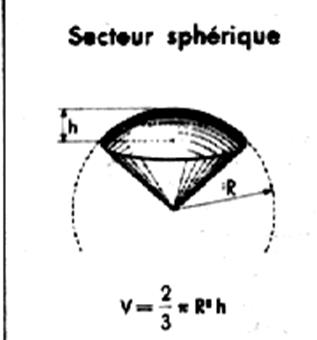
Secteur sphérique |
|
|
|
|