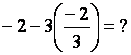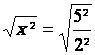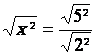Mathématiques :
(donné à Wassigny 02)
Manque de précisions :
dans quel ensemble de nombres travaille – t- on ? les
entiers naturels ou les nombres relatifs ?
Le 15/ Décembre /2010
|
|
|
>>>Info
>Résoudre
les principaux types d'équations du premier degré à une inconnue. |
|
|
|
Exercice
1 : résoudre |
>>> Info Voir : la leçon « résoudre » |
|
|
|
a) – 4 + 3 ( x -1) = 5 ( 2 – 4
x ) |
Autre méthode |
|
|
|
Solution 1 |
Solution 2 |
|
|
|
1°) développer dans les deux membres : -4 + 3 x - 3 = 10 – 20 x 2°) déplacer les « x » dans le premier membre (ne pas oublier
de changer de signe) -4 + 3 x - 3 + 20 x =
10 3°) Déplacer les nombres du premier membre dans le
deuxièmes membre. (ne pas oublier de changer de signe) 3 x+20x = 10 + 4 + 3 4°) 23 x = 17 5°) La
fraction est irréductible parce « 23 » et « 17 » sont des
nombres premiers en eux (ils n’ont pas de diviseur commun …) |
1°) Développer dans les deux membres : 4 + 3 x - 3 =
10 – 20 x 2°) Transformer les
expression en somme algébrique : ( -4) + ( - 3) + ( +3x) = ( + 10 ) + ( - 20 x) 3°) Neutraliser le
(-20x) du second membre (on
ajoute ( +20x) dans les deux membres.) ( -4) + ( +3x) + ( + 20
x) = ( + 10 ) + ( - 20 x) + ( + 20x) ( - 20 x) et ( + 20x) = 0 ( -4) + ( -3) + ( +3x) + ( +
20 x) = ( + 10 ) + 0 on calcule et on
remplace : ( -4) + ( -3) ; = (
- 7) On
calcule et on remplace : ( +3x) + ( + 20
x) ; = ( + 23 x) On
obtient l’égalité :
( - 7 ) + ( + 23 x) = (
+ 10 ) On
neutralise le ( -
7 ) dans le premier membres …..en ajoutant ( +7)
dans chaque membre) ( - 7 ) + ( +7) + ( + 23
x) = ( + 10 ) + ( +7) on sait que ( - 7 ) + ( +7) = 0 ;
et ( + 10 ) + ( +7) = ( + 17) donc :
( +7) + ( + 23 x)
= ( + 10 ) + ( +7) devient :: ( + 23 x) = ( + 17 ) |
|
|
|
b)
7 ( 5 x – 8 ) = - 56 + 35 x |
|
|
|
|
Solution 1 : 7 ( 5 x – 8 ) = - 56 + 35 x devient : 35 x – 56 = - 56 + 35 x on met les « x » d’un côté ,
les nombres de l’autre : on obtient , après transformations : (« un terme
change de membre , change de signe ») 56 + - 56 = + 35 x-35 x 0 = 0 x |
Solution 2 : 7 ( 5 x – 8 ) = - 56 + 35 x devient : 35 x – 56 = - 56 + 35 x On transforme les
deux expressions en somme algébriques : + ( +35 x) + (
– 56) = + ( - 56) + ( + 35 x) + ( +35 x) + (
– 56) = + ( - 56) + ( + 35 x) + ( +35 x) + (
– 35 ) = + ( - 35 x) + ( + 35 x) on opère dans les deux
termes 0 = Ox « toute valeur donnée à
« x » est solution » On peut dire qu’il y a une infinité de
solutions. |
|
|
|
c) 6 – ( 2 x – 4 ) =
3 + ( 7 x + 9 ) |
|
|
|
|
Solution
1 : 6
– ( 2 x – 4 ) = 3
+ ( 7 x + 9 ) on
supprime les parenthèses : on
obtient : 6
– 2 x + 4 = 3
+ 7 x + 9 puis : 10
– 2 x = 12 + 7x - 2
= 9 x ou
9 x = - 2 soit
|
Solution 2 : 6 – ( 2 x – 4 ) = 3 + ( 7 x + 9 ) on supprime les parenthèses : on obtient : 6 – 2 x + 4 = 3
+ 7 x + 9 puis : On transforme les deux expressions en somme
algébriques : (+ 6) + ( – 2 x)
+ ( + 4) = ( +3) + (+ 7 x) + ( + 9) ( + 10) + ( – 2 x) = ( +12) + (+ 7x) ( -
2) = ( + 9 x
) ou
( + 9 x) = ( - 2)
soit |
|
|
Exercice
2 : |
|||
|
|
niveau +++ Equation produit. et
« résoudre » dit
aussi « équation produit » |
|
|
|
|
a) ( x + 5 ) ( - 3 ) = 0 |
|
|
|
|
Remarques : 1) Nous avons dans le premier membre une
multiplication dont un facteur contient un terme en « x ». 2) Nous savons que dans une multiplication le produit est égal
à zéro si un des facteurs est égal à zéro… Dans cette équation donnée
, il suffit que x + 5 = 0 ; puisque « 0 fois ( -3) = 0 » Il faut résoudre l’équation : x + 5 = 0 x + 5 – 5 = - 5 x +
0 = - 5 x
= - 5 conclusion si x = - 5 ; alors ( x + 5 ) ( - 3 ) = 0 vérification : On remplace dans
l’équation de départ « x par (-5) » ( - 5 + 5 ) ( - 3 ) = 0 On transforme l’expression dans la
première parenthèse en somme algébrique ( ( - 5 ) + ( + 5 ) ) ( - 3 ) = 0 ; on remarque que ( (
- 5 ) + ( + 5 ) ) = 0 ( 0 ) ( - 3) = 0
, ce qui vérifie que si x = - 5 , l’équation est égale à zéro. |
|
|
|
|
b)
(
-
8 x + 5 ) ( - 2 – 3 x) = 0 |
|
|
|
|
Remarque : Nous avons dans le premier
membre une multiplication ( de 2 facteurs (
- 8 x + 5 ) et ( - 2 – 3 x ), dont les 2 facteurs contenant chacun un terme en
« x » : - 8
x et – 3 x ) , Nous savons aussi que dans une multiplication le produit est égal
à zéro si un des facteurs est égal à zéro… Dans cette équation donnée
, Nous avons le premier facteur : ( - 8 x
+ 5 ) Il faut que - 8 x + 5 = 0 Nous allons résoudre : - 8 x + 5 = 0 , On doit neutraliser le - 8 x dans le premier membre ( on ajoute + 8 x
de chaque côté ) ; Ce qui nous donne
: - 8 x + 5 + 8 x = +
8x après une transformation on
obtient : 5 = 8 x
ou 8 x = 5 solution 1 : Et
le deuxième facteur : ( - 2 – 3 x ) Il faut que - 2 – 3 x = 0 Nous allons résoudre : - 2 – 3 x = 0 , On doit neutraliser le - 3 x dans le premier membre ( on ajoute + 3 x
de chaque côté ) ; Ce qui nous donne
: - 2 - 3 x + 3 x = +
3 x après une transformation on
obtient : - 2 = 3
x ou 3 x
= - 2 solution 1 : conclusion : si = En plus : vérification n °1 : On remplace dans
l’équation de départ « x par ( - 8
fois on calcule : ( - 8
fois vérification n °2 : On remplace dans
l’équation de départ par ( - 8 fois on calcule : (( -
2 – 3 fois
( - 2 ) – (-2) = ( - 2 ) + ( +2)
= 0 |
|
|
|
|
Exercice 3 : ( pb de précision dans l’énoncé : « 8 » est un nombre
entier ? , ou « 8 » est la valeur absolue du nombre relatif
(+8) ? ) |
||
|
|
Solution
1 : « 8 » est un nombre entier naturel . a)
x² = 8 ; que l’on doit penser : x² = (+ 8) |
||
|
|
x² = 2 ( 4 ) et
|
||
|
|
Solution
2 : « 8 » est la valeur absolue du nombre entier relatif ( +8) Alors ,
il y a une double solution : . |
Info cours : opérations
.. ;;racines carrées des nombres relatifs. |
|
|
|
Se souvenir d’exemples de décompositions en produit
de facteurs intégrant un carré … : 8 = 2 fois 4 = 2
fois 2² 18 = 2 fois 9 = 2 fois 3² 27 = 3 fois 9 ; soit = 3 fois
3² ; ou = 3 3
50 = 2 fois 25 (et 25 = 5²) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b ) 4 x² = 25 ( pb de précision dans
l’énoncé : « 4 et 25 » sont des nombres entiers ? , ou
« 4 et 25 » sont les valeurs absolues du nombre relatif (+4) et
( +25) ? ) Ce qui conduit à deux
cas possibles et des solutions
différentes : |
|
|
|
|
Cas 1 : « 4 et 25 » sont
des nombres entiers Remarques : 4 = 2² et
25 = 5²
cas 1 : solution : x = 2,5 |
|
|
|
|
Cas
2 : « 4
et 25 » sont les valeurs absolues du nombre relatif (+4) et ( +25) ) Donc : ( + 4) est
obtenu avec le calcul de ( + 2) ² ou ( - 2) ² et (+ 25) est obtenu avec le calcul de ( +5)² ou ( -5)² ce qui conduit à deux
solutions possibles : x = ( +2,5) et x = ( - 2,5) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Exercice
4 : |
|
|
|
|
a) ( 3 x – 2 )
² + ( 3 x – 2) ( x + 3 ) = 0 |
|
|
|
|
Réponse : |
|
|
|
|
( 3 x – 2 ) ² +
( 3 x – 2) ( x + 3 ) = 0 peut s’écrire : ( 3 x – 2 ) ( 3 x – 2) + ( 3 x – 2) ( x +
3 ) = 0 Le premier membre comprend
deux termes , pour que le premier membre est égal à « 0 »
il faut que les deux termes soient égal à 0. - premier terme : (3 x
– 2 ) ( 3 x – 2) ( 3 x – 2) = 0 ;
3x = 2 ; donc - deuxième terme : il
faut que ( 3 x – 2) ( x + 3 ) = 0 le premier facteur est égal
à 0 si :
(voir ci-dessus)
( 3 x – 2) = 0 ;
3x = 2 ; donc et le deuxième facteur est égal à 0 si ( x + 3 ) = 0 ; oit x
= - 3 Conclusion : ( 3 x – 2 ) ² + ( 3
x – 2) ( x + 3 ) = 0 si |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b)
( 3 x – 2 ) ( 4 x + 1 ) = 0 |
|
|
|
|
( 3 x – 2) ( 4 x + 1 ) = 0 ; nous sommes en présence d’un
produit de facteurs : Nous savons qu’un produit
de facteurs est nul ( = 0) si un des facteurs est
nul. Donc nous allons rechercher
pour chaque facteur , la valeur de « x »
qui neutralise ce facteur : ( 3 x – 2) [ 4 x + 1 ] = 0 On pose et on résout :
a) ( 3 x – 2) = 0 ;
3x = 2 ; donc et b) ( 4 x + 1 ) = 0 ; 4 x = - 1 ; donc x = Conclusion : ( 3 x – 2 ) ² + ( 3
x – 2) ( x + 3 ) = 0 si |
|
|
|
|
Exercice 5 : |
|
|
|
|
Voir les pb? |
|
|
|
|
|
|
|
|
|
|
|
|