|
|
CORRIGE |
|
Classe de quatrième |
|
|
|
( 2014…) |
|
|
|
|
|
|
|
|
|
|
Pré requis: |
|
|||
|
·
SEGMENT |
||||
|
·
BIPOINT |
||||
ENVIRONNEMENT du dossier:
|
Objectif suivant : |
DOSSIER N° Fiches sur
la PROJECTION.
|
|
Fiche 1 : Projection sur une droite selon
une direction donnée. |
|
|
|
Fiche 2
Image d’une figure. |
|
|
|
Fiche 3 : Projection d’un segment et du milieu de
ce segment .(propriété 7 ) |
|
|
|
Fiche 4 : Une utilisation de la propriété ( 7 ) sur Projection
d’un segment et du milieu de ce segment. |
|
|
|
|
|
|
TEST |
COURS |
Interdisciplinarité |
|
|
|
|
|
|||||||||||
|
|
Fiche 1 : Projection sur une droite selon
une direction donnée. |
|
|
||||||||||
|
|
|
|
|||||||||||
|
|
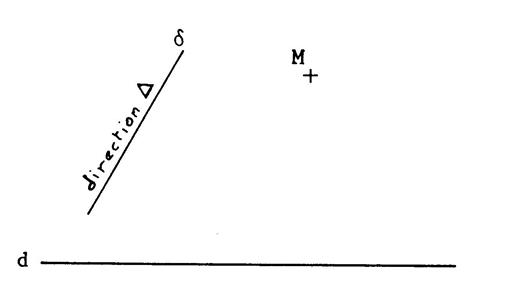
ci-contre : une droite « d » et
une direction « « M » étant un point quelconque du plan , tracez par « M » la droite de direction « ( C'est-à-dire la parallèle à « δ ») Cette droite est unique ( axiome
d’Euclide). Elle coupe
« d » en « M’ ». ( on est certain qu’elle coupe « d » car
elle n’a pas la même direction que
« d » ) |
|
|
||||||||||
|
|
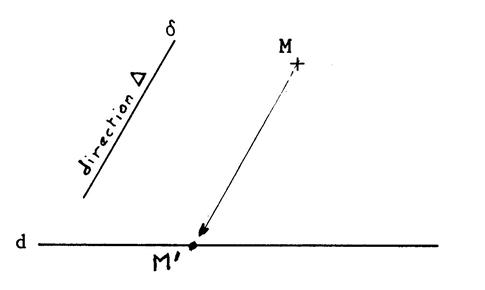
Vocabulaire : -
Le point
« M’ » ainsi obtenu est appelé
le projeté de « M » selon la direction « -
« -
La droite ( M M’ ) est la projection de
« M ». Dans ces conditions on dit que : « M’ » est l’image ( ou le projeté) de « M » dans la projection de
« d » selon la direction « |
|
|||||||||||
|
|
|
|
|||||||||||
|
|
|
La
flèche : M Lire : « M » à pour image « M’ » |
|
||||||||||
|
|
|
||||||||||||
|
|
|
||||||||||||
|
|
|
|
|||||||||||
|
|
Activité n°… : |
|
|||||||||||
|
|
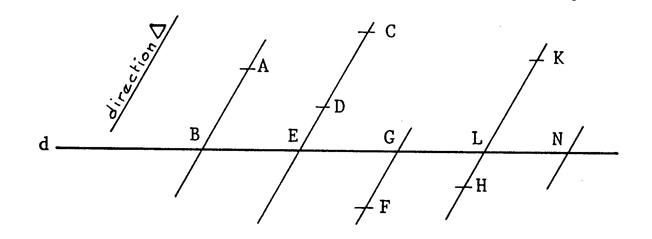
Sur la figure
ci-dessous , toutes les droites sauf
« d » ont la même direction de « Donnez les images des différentes points dans la
projection sur « d » de direction de « Ainsi : « M’ » étant le projeté de « M » ,
on écrira schématiquement : M |
|
|||||||||||
|
|
M |
|
|
||||||||||
|
|
C |
|
|||||||||||
|
|
A |
|
|||||||||||
|
|
D |
|
|||||||||||
|
|
F |
|
|||||||||||
|
|
K |
|
|||||||||||
|
|
H |
|
|||||||||||
|
|
N |
|
|||||||||||
|
|
|
|
|||||||||||
|
|
Remarque : Les points « C » et « D » ont
le même …nom……Le projeté de
« N » est …N……… Tous les points situés sur une droite de
direction « |
|
|||||||||||
|
|
|
|
|||||||||||
|
|
Activité n° 2 : |
|
|||||||||||
|
|
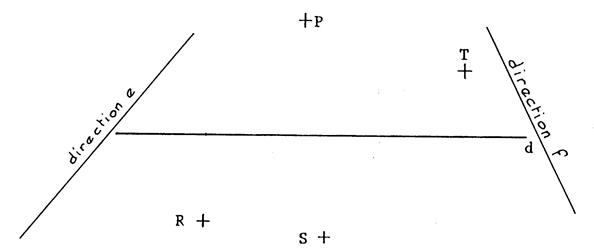
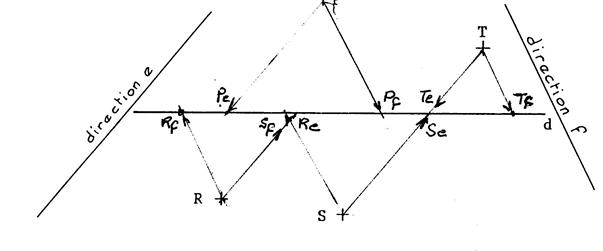
Déterminez les projetés des points « P » , « R » , « S » et « T ».
dans les deux cas suivants : 1°) Projection sur « d » de direction
« e ». 2°) Projection sur « d » de direction
« f » . Donnez un nom à ces points et complétez le dessin ci-dessous. |
|
|||||||||||
|
|
|
|
|||||||||||
|
|
Projection de direction « e » |
Projection de direction «
f » |
|
|
|||||||||
|
P |
P |
||||||||||||
|
R |
R |
||||||||||||
|
S |
S |
||||||||||||
|
T |
T |
||||||||||||
|
|
|
|
|||||||||||
|
|
Activité n° 3 : |
|
|||||||||||
|
|
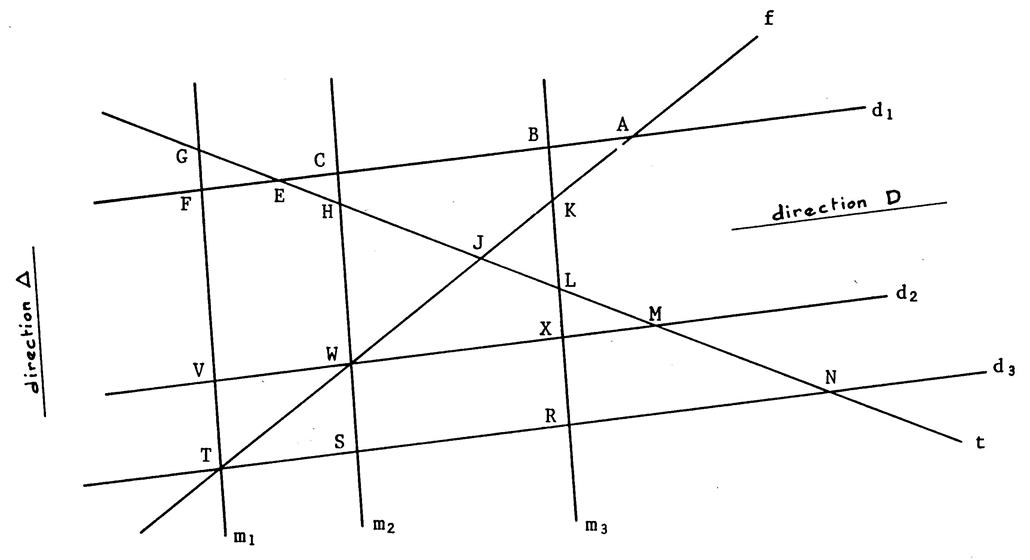
« d 1» ,
« d2 » et « d3 » sont des droites de direction
« D ». « m 1» ,
« m 2 » et « m 3 » sont des droites de direction « |
|
|||||||||||
|
|
|
|
|||||||||||
|
|
|
|
|||||||||||
|
|
Donnez le nom du projeté du point correspondant
dans les différents cas : |
|
|||||||||||
|
|
|
|
|||||||||||
|
|
Projection sur « t » direction « D » |
|
Projection sur « f » direction « |
|
Projection sur « f » direction
« D » |
|
|||||||
|
A |
S |
|
R |
V |
|
K |
J |
||||||
|
W |
G |
|
C |
B |
|
F |
A |
||||||
|
J |
X |
|
H |
A |
|
R |
X |
||||||
|
C |
R |
|
J |
G |
|
M |
N |
||||||
|
|
|
|
|||||||||||
|
|
|
|
|||
|
|
Fiche 2
Image d’une figure. |
|
|||
|
|
|
|
|||
|
|
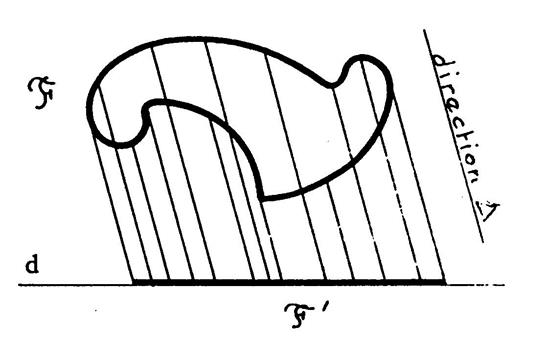
Dans la projection sur « d » selon la direction , l’image de « F » est la figure « F ’ » constituée par l’ ensemble des points qui
sont les projetés des points de
« F » . Dans cet exemple l’image de « F ’ » est
un …segment… |
|
|
||
|
|
Cas
général : Le projeté d’une figure sur une droite est cette droite toute entière
ou une portion de cette droite. |
|
|||
|
|
|
|
|||
|
|
v Image d’une droite : |
|
|||
|
|
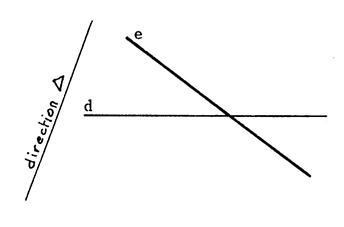
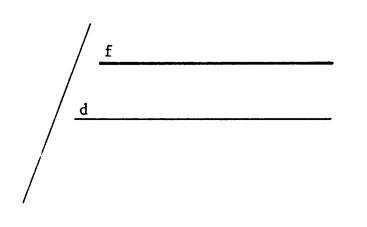
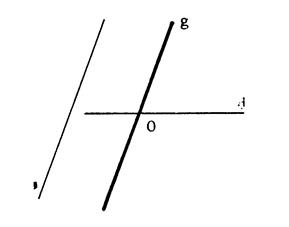
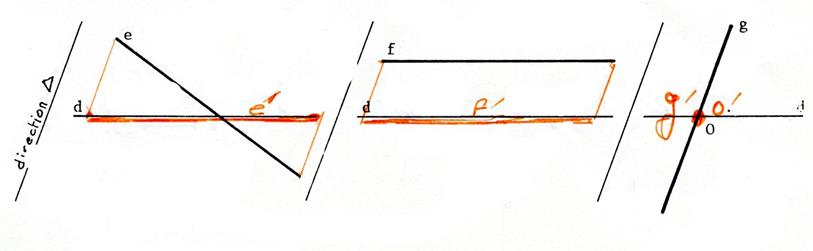
Dans les trois cas ci-dessous ,
dessinez en rouge l’image des droites
« e », « f » , et « g » dans la
projection sur la droite « d » selon la direction « |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Fiche 3 : Projection d’un segment et du
milieu de ce segment . |
|
|||
|
|
(ce cours débouche sur une propriété qui sera utilisée
par la suite sur les milieux …) |
|
|||
|
|
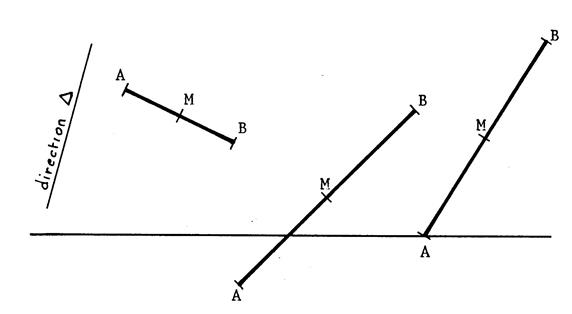
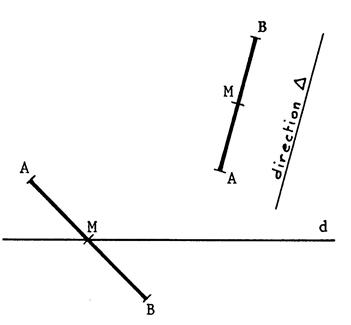
On donne une droite « d » et une direction
« [ AB ] est un segment de
« M » son milieu . Dans la projection de [ AB ] sur « d » suivant la direction
« Déterminez
« A ‘ » , « B ‘ » et
« M’ » , dans chacun des cas suivants ci-dessous . |
|
|||
|
|
|
|
|||
|
|
|
|
|
||
|
|
|
|
|||
|
|
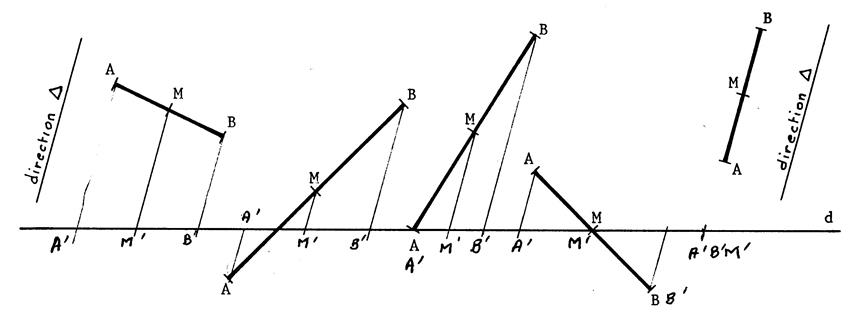
Vous constatez que dans tous les cas , le projeté du segment [AB]
est le segment [ A’ B’] et que le milieu de [ A’ B’] est le point
« M’ » qui est le « projeté » de « M », milieu de
[AB] . Nous énoncerons la propriété suivante que nous
admettrons : |
] |
|||
|
|
Propriété 7 : Dans toute projection sur une droite suivant une
direction donnée, ( la droite n’ayant pas pour
direction la direction de la projection), le projeté d’un segment est un
segment , le milieu du segment se projette au milieu du projeté de ce segment
. |
|
|||
|
|
|
|
|||
|
|
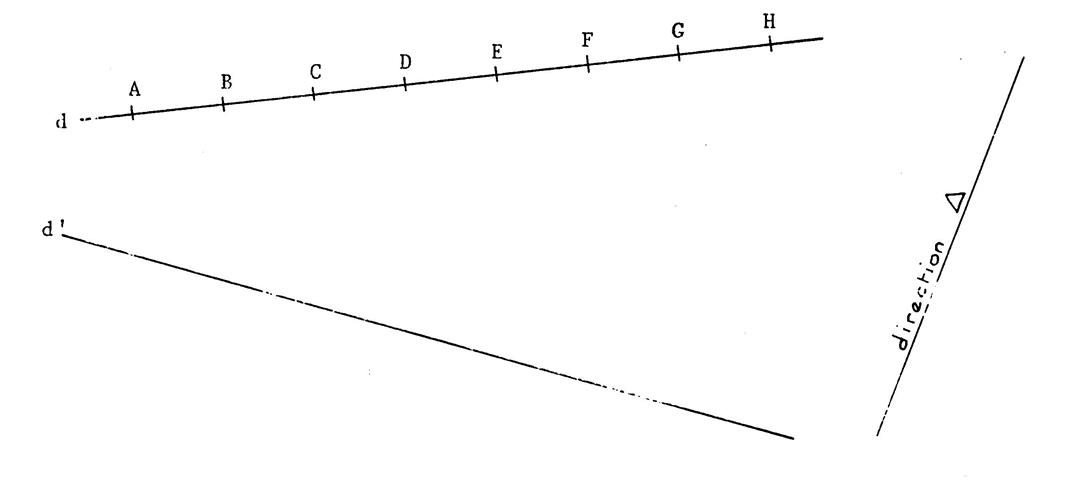
Activité n°… : Sur la droite « d » , les points
« A » , »B », « C » , « D » ,
« E » , « F » , « G » , « H »
déterminent une graduation
régulière. C'est-à-dire que « AB = BC = CD = DE = EF =
FG =GH ». En projetant la droite « d » sur la droite
« d’ » suivant la direction
« Les points « A » , »B »,
« C » , « D » , « E » , « F » ,
« G » , « H » ont respectivement pour projetés « A’ » , « B ‘ »,
« C’ » , « D’ » , « E’ » , « F’ » ,
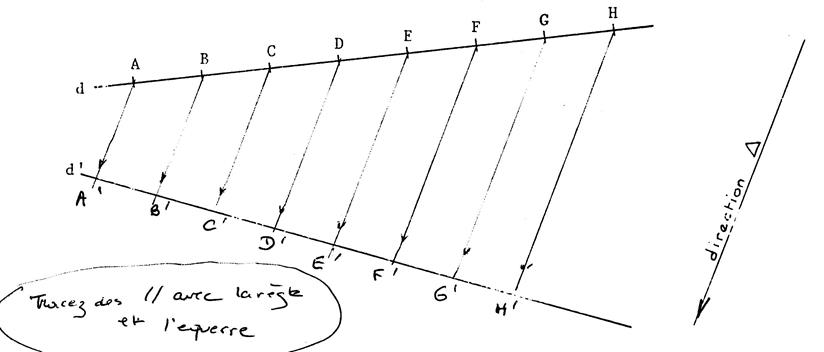
« G’ » , « H’ ». Faites le dessin….. |
|
|||
|
|
|
|
|||
|
|
Que pouvez-vous dire de la graduation ainsi
obtenu ?????? ( les graduations son régulière , la distance entre chaque
graduation est identique) ; Dites cela oralement … ; |
|
|||
|
|
|
|
|||
|
|
Fiche 4 : Démonstration : Une
utilisation de la propriété ( 7 ) sur Projection
d’un segment et du milieu de ce segment : |
|
|||
|
|
|
|
|||
|
|
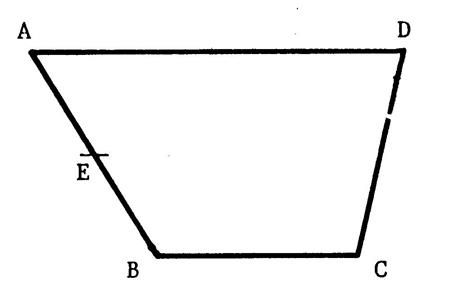
« ABCD » ,
ci-contre est un trapèze dans lequel ( AD ) et ( BC ) sont parallèles. On appelle « E » le milieu de [ AB ]. Par « E3 on mène la parallèle aux droites ( AD ) et ( BC ). Cette droite coupe ( DC ) en
« F ». Activité : Achevez la figure
. |
|
|
||
|
|
|
|
|||
|
|
Nous allons démontrer que « F » est le milieu de [ DC ]. |
|
|||
|
|
|
|
|||
|
|
Rappel : Faire une démonstration
consiste très souvent à montrer que le
problème que l’on étudie se ramène à une situation connue. Ainsi dans le cas présent ,
si l’on peut trouver une projection telle que [ DC] soit le projeté de [ AB ] et que « F » soit le projeté du
point « E » milieu de [ AB ]
, alors on sera dans la situation
de la propriété « 7 » et la conclusion en découlera immédiatement. |
|
|||
|
|
|
|
|||
|
|
Analyse de la situation : |
|
|||
|
|
Ø Ce que l’on sait par hypothèse . On écrit ( après
traduction) les données du problème |
|
|
||
|
|
|
|
|||
|
|
Ø Ce que l’on veut démontrer ( conclusion) :
« F » est le ……milieu de [ DC] ….. |
|
|||
|
|
|
|
|||
|
|
Ø Recherche. ( à ne pas écrire dans un devoir ) |
|
|||
|
|
Pour faire apparaître la situation de la
propriété « 7 », il faut faire intervenir une projection. On
imagine que l’on projette la droite ( AB ) sur la droite (DC) , la
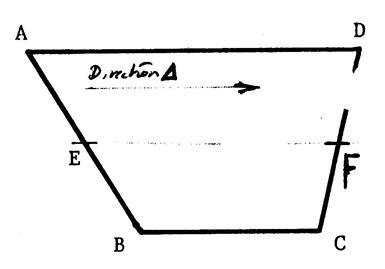
direction de projection étant celle des droites parallèles ( AD ) , ( BC ) , ( EF ) . Le segment [ AB ] a alors pour projeté le segment ………[ DC ]…….. « E » étant le milieu de [ AB ] , on se trouve bien dans la situation de
la propriété « 7 » donc le point « F » qui est le projeté
du milieu de « E » de [ AB
] est le milieu de ………[ DC ]…….. |
|
|||
|
|
|
|
|||
|
|
Rédaction de la démonstration. |
|
|||
|
|
( C’est ce que vous devez écrire dans un devoir ) et ( n’oubliez pas de
justifier toutes les affirmations) |
|
|||
|
|
Les droites
( AD ) , ( BC ) et ( EF ) sont parallèles ( par hypothèse ) elles ont donc même ….direction…. Considérons
la projection de (AB ) sur ( DC ) dont la direction de projection est
celles des droites parallèles ( AD ) ,
( B C ) et ( EF ). « A » a pour projeté : « D ».. ;
« B » a pour projeté .. « C »…. ; « E » a pour projeté .. « F
»…. Le projeté de [ AB
] est donc ………[
DC ]…….. . Par hypothèse
« E » est le milieu de [
AB ]
. D’après la propriété « 7 » (vu dans la fiche « 3) , le milieu de « E » de [ AB ] se projette au milieu de …………[ DC ]……..
……or, le projeté de « E » est ….« F ».., donc « F » est …le milieu de …………[ DC ]…….. |
|
|||
|
|
|
|
|||
|
|
Activité n°…. |
|
|||
|
|
|
|
|||
|
|
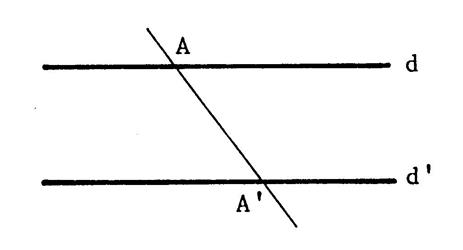
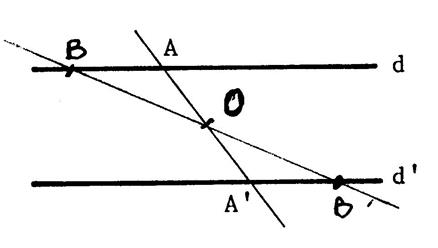
Les droites « d » et « d’ »
sont deux droites parallèles. « A » est le point de « d » , « A’ » un point de « d’ » . Soit « O » le milieu de [ AA’ ] . Placez ce point. Une droite passant par « O » coupe
« d » en « B » et « d’ » en « B’ ». Démontrez que « O » est le milieu
de [ BB’ ] |
|
|
||
|
|
|
|
|
||
|
|
Plan de la Démonstration : Hypothèse :………….. |
|
|||
|
|
Conclusion : …………………………… |
|
|||
|
|
|
|
|||
|
|
Démonstration : Considérons la projection de ( AA’) sur ( BB’) dont la direction de projection
est ………………………………………. |
|
|||
|
|
|
|
|||