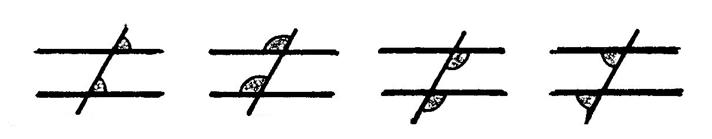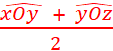|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ENVIRONNEMENT
du dossier:
DOSSIER:
« les
ANGLES » ( classe de collège 5ème)
|
|
|
|
|||||
|
|
Fiche 1 : Opérations sur les angles : Somme d’angles, Différence d’angles, Produit d’un angle par lui-même. |
|
|||||
|
|
Fiche 2 : Angles adjacents. |
|
|||||
|
|
Fiche 3 : Angles complémentaires. |
|
|||||
|
|
Fiche 4 : Angles supplémentaires. |
|
|||||
|
|
Fiche 5 : Angles opposés par le sommet. |
|
|||||
|
|
Fiche 6 : Droites parallèles coupées par une
sécante. ( angles alterne …..correspondants….) |
|
|||||
|
|
Fiche 8 : Bissectrice. A
) Bissectrices de deux angles adjacents supplémentaires. B ) Bissectrices d’angles opposés par le sommet. |
|
|||||
|
|
Fiche 9 : Angles du parallélogramme. |
|
|||||
|
|
Fiche 10 : Construction d’un angle
donné. ( sans
rapporteur ) |
|
|||||
|
|
|
|
|||||
|
|
|||||||
|
|
|
||||
|
|
Fiche 1 : Opérations sur les angles. |
|
|||
|
|
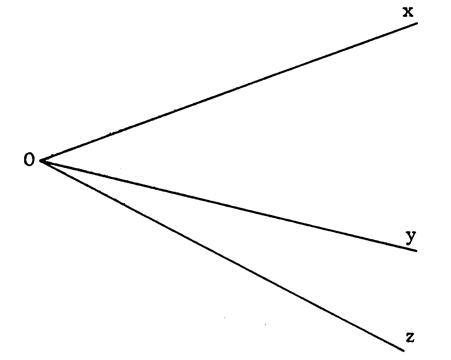
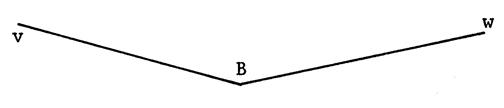
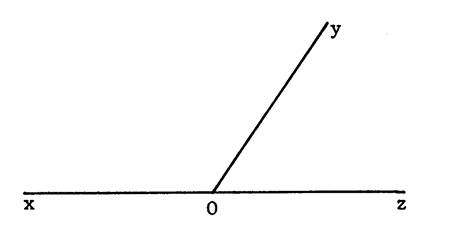
Somme d’angles : |
|
|||
|
|
Mesurez à ( 1° prés) : Vous trouvez : Vous pouvez écrire alors : On dit que : Et on écrit : |
|
|
||
|
|
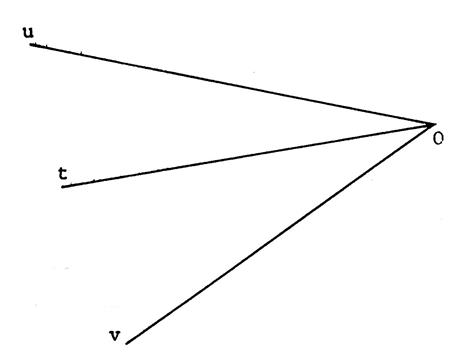
Différence d’angles . |
|
|||
|
|
Mesurez à ( 1° prés
) : Vous trouvez : On peut écrire
alors : On dit que : Et on écrit
: |
|
|
||
|
|
|
|
|||
|
|
Activité n°….. |
|
|||
|
|
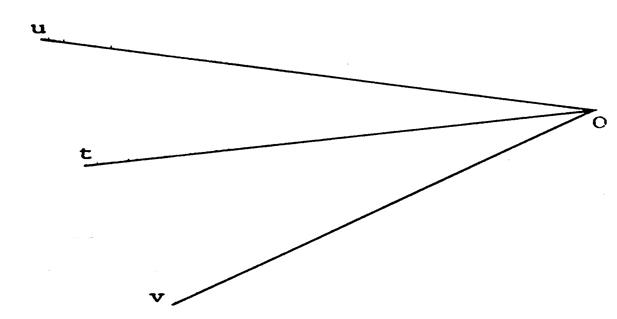
La figure ci-contre donne la valeur de certains
angles. Sachant que
|
|
|
||
|
|
|
|
|||
|
|
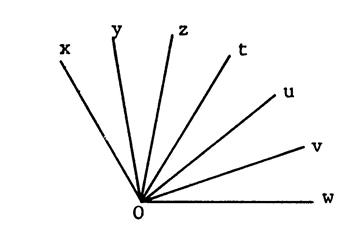
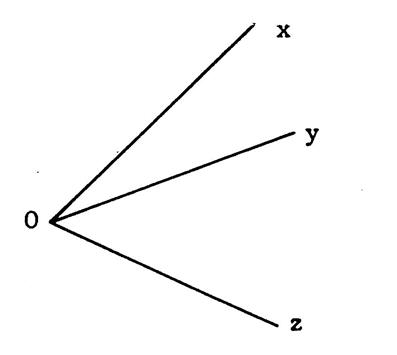
Produit d’un angle par lui-même. |
|
|||
|
|
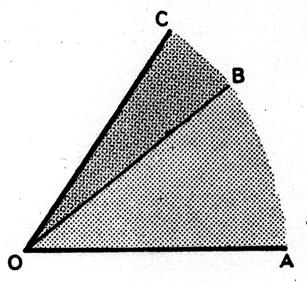
La figure ci-contre représente 6 angles égaux.
On peut écrire
alors : |
|
|
||
|
|
|
|
|||
|
|
Activité n°…….. |
|
|||
|
|
· Complétez : |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
· |
|
|||
|
|
· Trouvez sur la figure d’autres
angles égaux à |
|
|||
|
|
· Trouvez sur la figure des angles égaux
à |
|
|||
|
|
· · |
|
|||
|
|
· · Nommez des angles de la figure
égaux à |
|
|||
|
|
|
|
|||||||
|
|
Fiche 2 : Angles adjacents. |
|
|||||||
|
|
|
|
|||||||
|
|
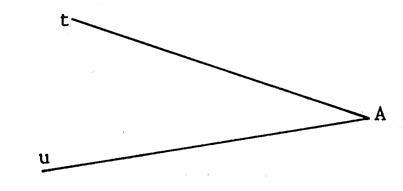
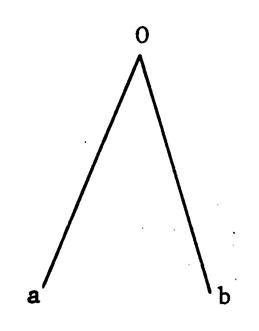
Les angles
Cela signifie : -
Ils ont le même
sommet : « O » -
Ils ont un côté
commun : [ Oy -
Les autres côtés sont
de part et d’autre du côté commun. |
|
|
||||||
|
|
Activité n°…… |
|
|||||||
|
|
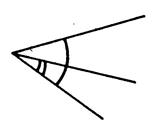
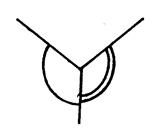
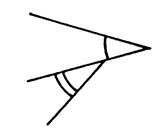
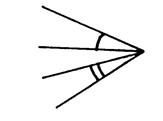
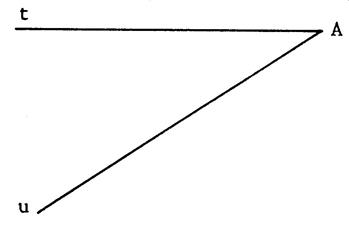
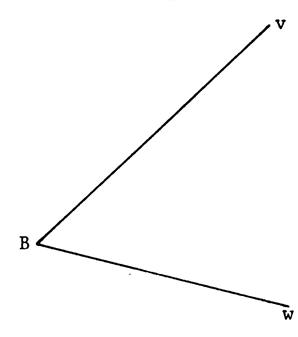
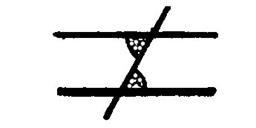
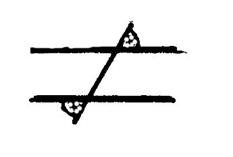
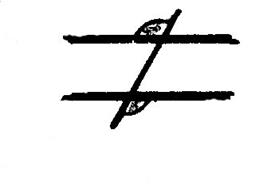
Parmi les dessins ci-dessous ,
reconnaissez les angles adjacents. |
|
|||||||
|
|
Les deux angles que vous devez considérer sont repérés par des petits
arcs (ci-contre ) |
|
|
||||||
|
|
Répondre par « oui » ou
« non » |
|
|||||||
|
|
Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
Figure 5 |
|
|||
|
|
|
|
|
|
|||||
|
……oui…… |
oui |
oui |
non |
non |
|||||
|
|
|
|
|||||||
|
|
|
|
|||
|
|
Fiche 3 : Angles complémentaires. |
|
|||
|
|
|
|
|||
|
|
A
retenir : On appelle « angle
complémentaires » deux angles dont la somme est égale à 90° |
|
|||
|
|
|
|
|||
|
|
· On dit que l’angle de 39 ° a
pour complément l’angle de : 90°- 39° = 51° |
|
|||
|
|
|
|
|||
|
|
· Contrôlez en mesurant que les angles ci-contre sont apparemment
complémentaires. |
|
|
|
|
|
|
· Dessinez ci-dessous deux angles adjacents complémentaires
Les côtés [ Ox et
[ Oz sont …………………..perpendicuaires…. |
|
|||
|
|
Activité n° …….. |
|
|||
|
|
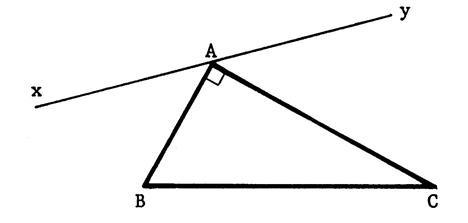
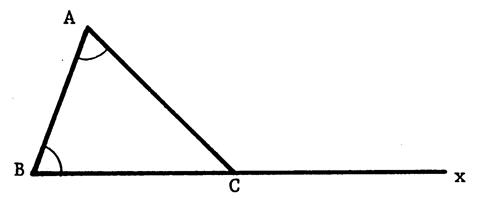
« ABC »
est un triangle rectangle en « A ». « xy » est une droite quelconque passant par
« A »ne coupant pas [ BC ]. Prouvez que |
|
|
||
|
|
|
|
|||
|
|
Activité n° …….. |
|
|||
|
|
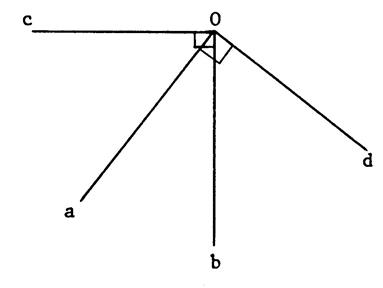
Considérons
la figure ci-contre [ O d est perpendiculaire à [ Oa [Oc est perpendiculaire à [ Ob Prouvez en les calculant que |
|
|
||
|
|
D’une manière générale ,
on prouverait de même que : Si deux angles ont le même complément alors ils
sont ………………………………………….. |
|
|||
|
|
|
|
||||
|
|
Fiche 4 : Angles complémentaires. |
|
||||
|
|
|
|
||||
|
|
A retenir : On appelle « angles
supplémentaires » deux angles dont la somme est égale à 180° |
|
||||
|
|
|
|
||||
|
|
· On dit que l’angle de « 39° » a pour « supplément » l’angle de : 180 ° - 39° = 141° |
|
||||
|
|
· Un angle aigu a pour supplément un angle ………>
90°……………( et inversement ) |
|
||||
|
|
· Le supplément de l’angle droit est l’angle …droit…… · Si eux angles ont le même supplément alors ils sont ….égaux…….. |
|
||||
|
|
· Contrôlez en mesurant que les angles ci-contre sont apparemment
supplémentaires. |
|
|
|
||
|
|
|
|
||||
|
|
Dessinez ci-dessous deux angles adjacents
supplémentaires Les demi-droites [ O
x et [ Oz
sont opposées , c'est-à-dire que « xz »
est une …………………………………………….. |
|
||||
|
|
|
|
||||
|
|
Activités N°…….. |
|
||||
|
|
On donne un angle Tracez [ Oc perpendiculaire à [ Oa de telle sorte que Tracez [ Od perpendiculaire à [ Ob de telle sorte que Prouvez que ( Pour cela calculez |
|
|
|||
|
|
|
|
|||||||
|
|
Fiche 5 : Angles opposés par le sommet. |
|
|||||||
|
|
|
|
|||||||
|
|
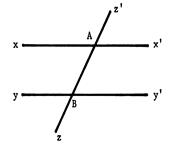
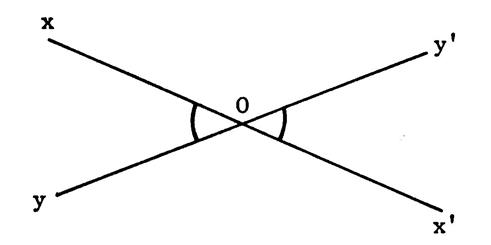
ci-contre , on vous
donne deux droites « xx’ »
et « yy’ » sécantes en « O ». Elles déterminent 4 angles. On dit que
les angles Il en est de même pour : Apparemment : |
|
|
||||||
|
|
C’est ce que nous allons prouver : |
|
|||||||
|
|
Puisque [ Ox et [ Ox’ sont opposées , les angles Puisque [ Oy et [ O y’
sont opposés , les angles Puisque les angles On prouverait de même pour |
|
|||||||
|
|
A retenir : Si deux angles sont opposés par le
sommet , alors ils sont ….égaux……. |
|
|||||||
|
|
|
|
|||||||
|
|
Remarque : On aurait pu le prouver autrement :
en utilisant le fait que « O » est
centre
de symétrie de la figure. |
|
|||||||
|
|
|
|
|||||||
|
|
Fiche 6 : Droites parallèles coupées par une
sécante. |
|
|||||||
|
|
|
|
|||||||
|
|
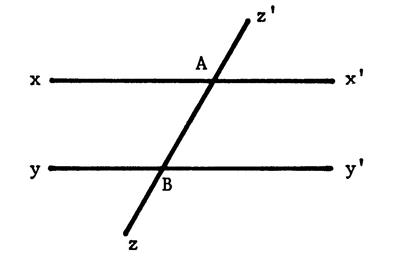
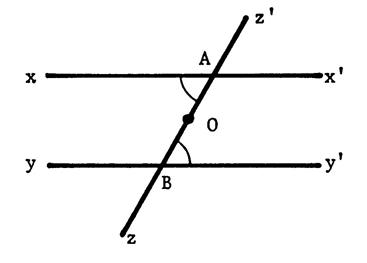
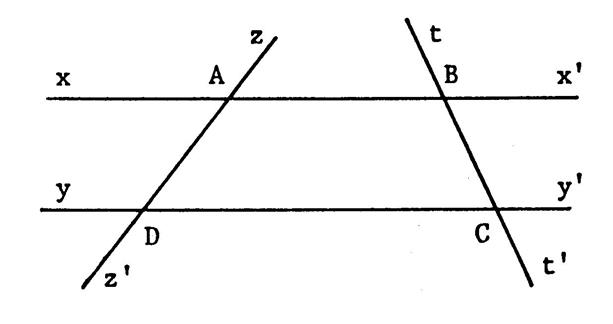
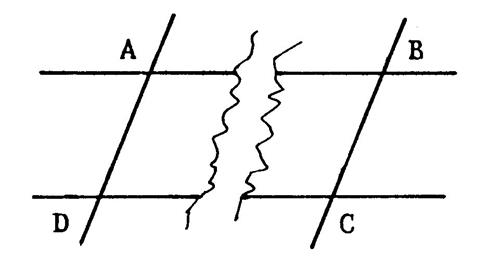
Voici ci-contre deux droites parallèles xx’
et yy’ . Une droite zz’ coupe xx’
en « A » et yy’ en « B ». Vous êtes en présence d’une figure appelée :
« parallèles coupées par une
sécante ». Apparemment il y a sur cette figure des angles
égaux. ( vous pouvez mesurer) |
|
|
||||||
|
|
Activité n°…. |
|
|||||||
|
|
Passez en bleu les angles égaux à l’angle |
|
|||||||
|
|
|
|
|||||||
|
|
· Les mesures étant toujours imprécises et les apparences souvent trompeuses , pour pouvoir affirmer ce que l’on énonce , il
est indispensable de faire un
raisonnement . |
|
|||||||
|
|
Nous allons prouver par un raisonnement que les angles Appelons « O » le milieu de [ AB ]. Dans la symétrie de centre « O » , |
|
|
||||||
|
|
Le point « A » a pour symétrique le
point « B » . La droite zz’ a pour
symétrique ……………………………….. La droite xx’ passant par « A » a pour symétrie la droite passant par
« B » et qui lui est parallèle : C’est la droite …………………….. Le point « O » est donc centre de symétrie de la figure. L’ angle Or le symétrique d’un angle est un angle superposable . Donc les angles D’autre part De même Puisque Tous les angles bleus sont donc ……égaux……… On prouverait de même que les angles rouges sont ………….égaux……….. |
|
|||||||
|
|
Etant donné deux droites ( parallèles ou
non ) et une sécante , elle déterminent entres elles 8 angles. |
|
|||||||
|
|
Le tableau ci-dessous donne le nom de différentes positions de ces angles. |
|
|||||||
|
|
Les angles
considérés sont repérés par :
|
|
|||||||
|
|
|
Angles alternes internes |
|
|
|
|
|||
|
|
Angles alternes externes |
|
|
|
|||||
|
|
Angles correspondants. |
|
|
||||||
|
|
|
|
|||||||
|
|
A retenir : Deux droites parallèles coupées par une sécante
déterminent. -
Des angles alternes
internes…………………………………………… -
Des angles alternes
externes………………………………………….. -
Des angles
correspondants ………………………………………………. |
|
|||||||
|
|
|
|
|||||||
|
|
Activité n°…….. |
|
|||||||
|
|
« xx’ » et « yy’ »
sont deux droites parallèles. Sachant que ( expliquez
si vous passez un oral ).
|
|
|
||||||
|
|
|
|
||
|
|
Fiche 7 : Exercices sur les
« parallèles coupées par une sécante »…. |
|
|
|
|
|
|
|
||
|
|
Activité n° …. |
|
||
|
|
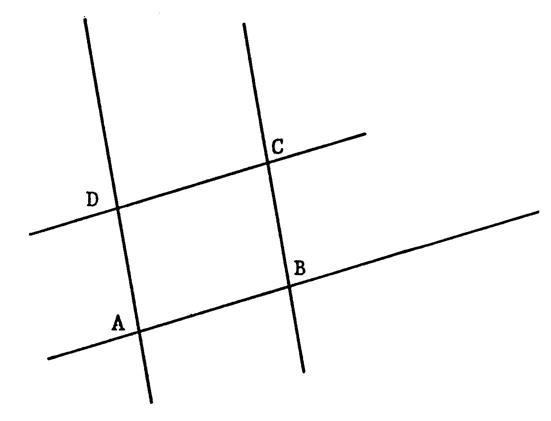
Ci-contre on a dessiné deux paires de droites
parallèles qui se coupent deux à deux en « A » ,
« B » , « C » et « D ». Tracez ( DB) et tracez par « C » la parallèle à ( DB ). Elle coupe ( AD ) en
« E » et ( AB ) en « F ». Coloriez en vert les angles égaux à Coloriez en rouge les angles égaux à Coloriez en bleu les angles égaux à Conseil : ne colorier que la région du
sommet. A l’oral : expliquez pourquoi ces angles
sont égaux. |
|
|
|
|
|
Activité n° …. |
|
||
|
|
« ABC » est un triangle isocèle ( Tracez par « C » la demi-droite [ Cy parallèle à ( AB ) Prouvez que [ Cy est
bissectrice de l’angle |
|
|
|
|
|
|
|
|
|
|
Fiche 8 : Bissectrice. |
|
|
|
|
A ) Bissectrices de deux angles adjacents supplémentaires. |
|
|
|
|
Tracez les bissectrices : [Ou de Mesurez l’angle Remarque : les mesures reste imprécises… Nous allons faire un raisonnement pour trouver ce
résultat.. |
|
|
|
|
[Ou étant
bissectrice de …… [ Ov étant bissectrice de ……
|
|
|
|
|
A retenir : Les bissectrices de deux angles adjacents
supplémentaires ont leurs supports ………qui forment un
angle droit………………….. |
|
|
|
|
|
|
|
|
|
B ) Bissectrices d’angles opposés par le sommet. |
|
|
|
|
|
|
|
|
|
« xx’ » et « yy’ »
sont deux droites se coupant en « O ». Tracez les bissectrices [ Ou ; [ Ov ; [ Ow ; [ Ot ; des angles « apparemment » les demi-droites [Ou
et [Ow sont opposées ,
ainsi que les demi-droites …….. ………….
et constituent ainsi deux droites… Nous allons le prouver par le raisonnement : |
|
|
|
|
On prouverait de même que :
On en déduit alors que |
|
|
|
|
|
|
|
|
|
A retenir : · Les bissectrices de deux angles opposés par le sommet sont des demi-droites ………………… · Deux droites sécantes déterminent quatre angles dont les
bissectrices constituent deux droites
………………. |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Fiche 9 : Angles du parallélogramme. |
|
|
||
|
|
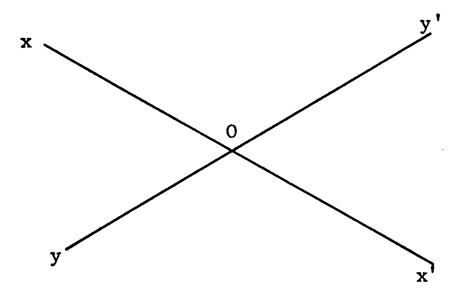
Les droites
( AB ) et ( DC ) sont parallèles. Les droites ( AD ) et (
BC ) sont parallèles. Le quadrilatère
« ABCD » est donc un
………..parallélogramme…. |
Figure 1
|
|
||
|
|
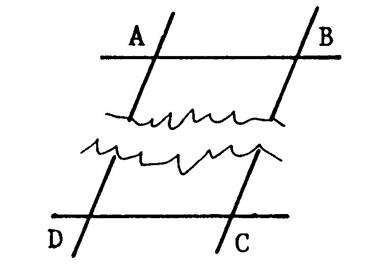
En imaginant que l’on découpe cette figure comme
ci-dessous , on se trouve en présence , dans les
deux cas , de deux fois « deux
parallèles coupées par une sécante ». |
|
|||
|
|
|
|
|
|
|
|
|
· Sur la « figure 1 » , coloriez la
région des sommets , passez en bleu les angles égaux à
SA l’oral : Expliquez pourquoi un angle bleu et un angle rouge sont
supplémentaires. |
|
|||
|
|
Vocabulaire : Pour le quadrilatère « ABCD », Il en est de même pour
Il en est de même pour On dira alors . |
|
|||
|
|
A retenir : Dans tout parallélogramme , Les angles opposés sont ……………égaux……….. Les angles consécutifs sont ………supplémentaires… |
|
|||
|
|
|
|
|||
|
|
Remarque : On peut obtenir ce résultat en
utilisant la symétrie
centrale . ( si vous
passez l’oral : expliquez !!!) |
|
|||
|
|
|
|
|||
|
|
Fiche 10 : construction d’un angle
donné. ( sans
rapporteur ) |
|
|||
|
|
|
|
|||
|
|
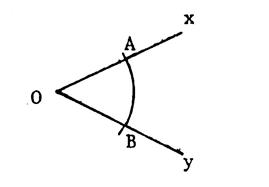
Figure ci-contre : on vous donne un angle On vous demande de reproduire cet angle sans utiliser de rapporteur. |
|
|
||
|
|
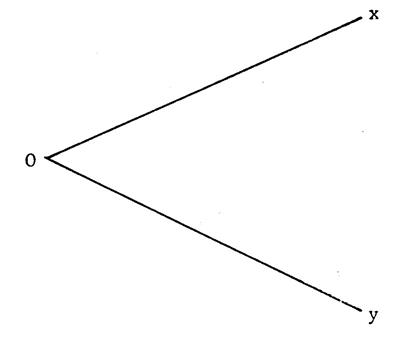
Procédure : Sur la figure ci-dessous : Tracez un arc de cercle de centre « O » . (voir la figure ci-dessus) Il coupe [ Ox
et [ Oy en
2 points « A » et « B » . Vous obtenez alors un triangle isocèle
« OAB ». Vous n’avez plus qu’à reproduire ce triangle ci-dessous . |
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
TRAVAUX AUTO
FORMATIFS.
CONTROLE :
Aucun
|
24°) Trouver deux angles
supplémentaires dont l'un soit le quadruple de l'autre. |
|
|
25°) Trouver deux angles complémentaires dont
l'un soit le double de l'autre. |
|
|
26°) mesurer
les angles ; les nommer. Etablir une égalité. |
|
|
|
|
|
|
|