|
Pour Aide et Formation Individualisée |
TRAVAUX SOMMATIFS |
|
||||||
|
|
Matière : MATHEMATIQUES |
|
||||||
|
Ces travaux ont
été en partie étudiés dans la leçon
sur « Pythagore » (cours niveau V) |
||||||||
|
TITRE : Calculs
sur les prismes droits |
||||||||
|
|
||||||||
|
NIVEAU : niveau V / NIVEAU
IV : |
OBJECTIFS : Travaux BILAN de fin de
formation en vu d’obtenir une
validation de la formation . |
|||||||
|
|
I ) Pré requis: (pour
remédiation ou mise à niveau) |
|
|
||||
|
|
|
|
|||||
|
|
|
|
|||||
|
|
|
|
|||||
|
N° 1 / |
CONSIGNES |
|||||||
|
|
La séquence ne doit pas dépasser 45
minutes. Matériel : le matériel habituel est autorisé :crayon ,
stylo, règle, rapporteur, compas,équerre, calculatrice. Ecrire à l’encre,
dessiner au crayon. (trait fin ,net , précis.) Le devoir est à rendre sur copie blanche. |
|||||||
|
|
TRAVAUX CONTROLE |
|
|
|
|
|
|
|
Les questions relatives à « ce qu’il faut
retenir » , au
« savoir » se reporter aux cours sur : |
|
|
|
Pythagore ; Aire d’un carré et d’un rectangle ,
volume d’un cube et d’une pyramide ;…revoir les notions sur la
représentation en perspective. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TRAVAUX :
EVALUATION |
|
APPLIQUATION :
PRISME DROIT
|
N° |
Figure |
Données : |
Réponse : |
|
|
|
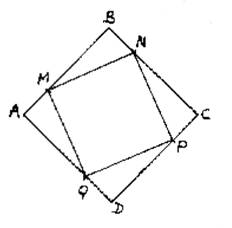
Soit le carré ABCD. On sait que : AB= AM = BN = CP = DQ = On demande : 1°) Calculer les
dimensions du carré MNPQ. 2°) Niveau + comparer les deux aires. |
|
|
N° |
Figure |
Données : |
Réponse : |
|
|
|
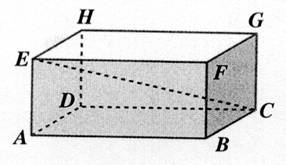
ADCB est la base du prisme.. Les dimensions du
parallélépipède rectangle sont : (en mm) L = 120 mm ; Largeur = Hauteur = Calculer la
longueur : EB = BG = EC = |
|
|
N° |
Figure |
Données : |
Réponse : |
|
|
|
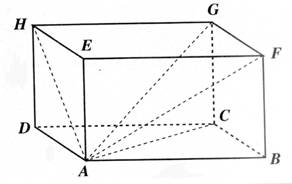
DCBA est la base du prisme.. Les dimensions du
parallélépipède rectangle sont : (en mm) L = 100 mm ; Largeur = Hauteur = Calculer la
longueur : HA = GA = FA = CA = |
|
PB NIVEAU IV :
|
N° 4 |
Figure |
Données : |
|
|
|
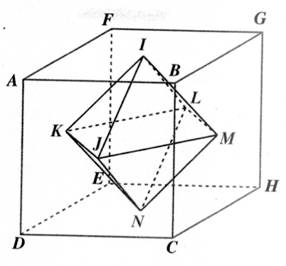
Soit un cube dont l’arête
mesure Les points I, J, K, L, M, N, sont les centres des faces du cube . a)
Combien de
faces a le solide « I J K L M N » ? Montrer simplement que toutes ses arêtes
sont égales. b)
Calculer la
longueur d’une arête , EM par exemple. c)
Calculer le volume
de la pyramide « KLMJI » , en déduire le volume du solide :
« I J K L M N » |