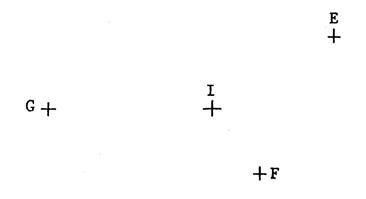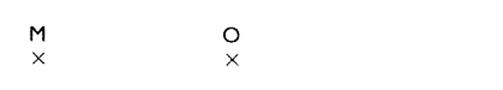|
|
|
Classe de 5ème collège |
|
|
|||||||||||||||||||||
|
|
|
|
( programme
5ème ) |
|
|||||||||||||||||||||
|
|
DOSSIER : SYMETRIE CENTRALE |
|
|
||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
|
Niveau. VI ; V |
|
||||||||||||||||||||||||
|
Pré requis: |
|
||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
Le point |
|
|||||||||||||||||||||||
|
Le cercle :et la symétrie centrale
(centre) |
|
|||||||||||||||||||||||
|
ENVIRONNEMENT du
dossier: |
|
|||||||||||||||||||||||
|
Objectif
précédent : P5 :voir activité sur la fiche 2 :repérage
et symétrie.. |
Objectif suivant : |
tableau : |
||||||||||||||||||||||
|
DOSSIER : SYMETRIE CENTRALE |
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
Fiche
1 : Découverte de la symétrie centrale . |
|
||||||||||||||||||||||
|
|
Fiche
2 : Construction de l’image d’un point . |
|
||||||||||||||||||||||
|
|
Figure
3 : Image d’une figure dans une symétrie centrale. |
|
||||||||||||||||||||||
|
|
Fiche
4 : Construction de l’image d’une figure. |
|
||||||||||||||||||||||
|
|
Fiche
5 : Ne pas confondre « symétrie centrale » et « symétrie orthogonale » |
|
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
TEST |
COURS |
Interdisciplinarité |
|
|||||||||||||||||||||
|
|
||||||||||||||||||||||||
|
|
Fiche 1 : Découverte de la symétrie centrale |
|
|
|||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
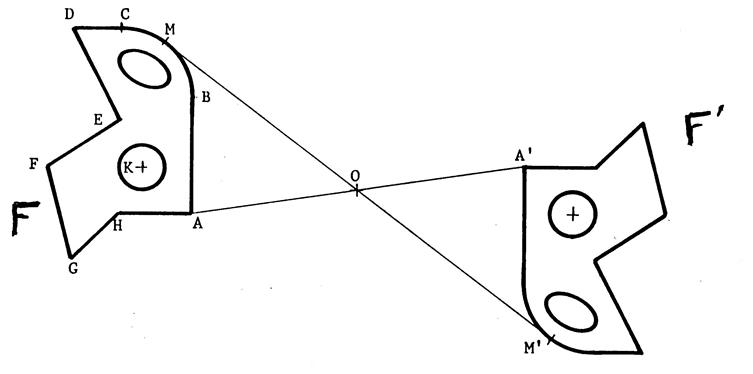
ci- dessus deux figures « F » et
« F’ » et un point « O ». Prenez la feuille de papier calque. Calquez la figure « F » , le point « O » et la figure
« F’ ». Sans bouger le calque ,
piquez la pointe de votre compas au
point « O ». Ensuite faîtes tourner le calque de telle sorte
que le dessin de « F » vienne sur « F’ ». Que constatez-vous pour « F’ » et le dessin de « F »et pour
« F » et le dessin de « F’ » ? |
|
||||||||||||||||||||||
|
|
On peut dire alors que : « F » a pour image « F’ » et « F’ »
a pour image « F » dans
une rotation de centre « O ». |
|
||||||||||||||||||||||
|
|
· Quel est l’angle de
rotation ? ……………………………………. Dans cette
rotation « A » a pour image « A’ » ,
vous pouvez dire alors que |
|
||||||||||||||||||||||
|
|
· On ferait le même raisonnement pour n’importe quel point : « M » étant un point quelconque de « M’ » son image dans cette rotation , alors
« O » est le milieu de |
|
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
Une telle rotation est appelée : « symétrie centrale de centre
« O » » Le point « O » est appelé « centre
de symétrie » . Quelle est son image ?
……………………….. Dans cette symétrie ,
« F’ » est appelée la « symétrie »
de « F ». La symétrie de
« F’ » est « F ». On dit alors que
« F » et
« F’ » sont symétriques par rapport à « O ». « A’ » qui est l’image de « A » est appelé le
« symétrique de « A ». Le symétrique de « A’ » est « A » . On dit alors que « A » et « A’ » sont symétriques par rapport à
« O ». |
|
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
· Placez sur « F’ » les points
« B’ » , « C’ » , « D’ » ,
« E’ » , « F’ » , « G’ » , « H’ » ,
« K’ » symétriques respectifs de « B » , « C »
, « D » , « E » , « F » , « G » ,
« H » , « K ». |
|
||||||||||||||||||||||
|
|
A retenir : |
|
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
Etant
donné un point « O » ( appelé :
centre de symétrie) , deux points
« M » et
« M’ » sont « symétriques par rapport à « O » »
signifie « O » est le milieu de |
|
|
||||||||||||||||||||
|
|
|
Deux figures sont symétriques par rapport à « O »
signifie : A chaque point « M » de l’une des
figures correspond un points « M’ »
de l’autre tel que « O » soit le milieu de |
|
|
||||||||||||||||||||
|
|
|
Deux figures symétriques par rapport à un point
sont superposables. |
|
|
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
Fiche 2 : Construction de l’image d’un point . |
|
|
|||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
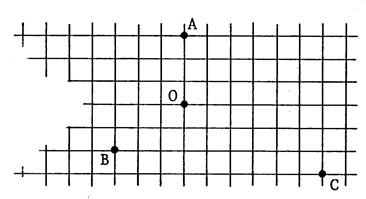
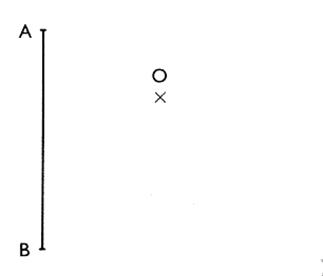
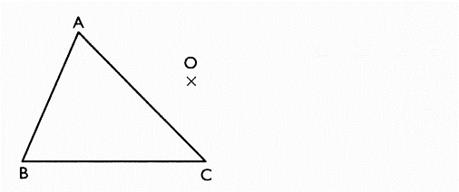
Exercice 1 :
En utilisant le quadrillage , construisez sur
la figue ci contre , les points « A’ » ,
« B’ », « C’ » symétriques par rapport à « O »
des points « A » ,
« B » , « C ». |
|
|
|||||||||||||||||||||
|
|
Exercice 2. |
|
||||||||||||||||||||||
|
|
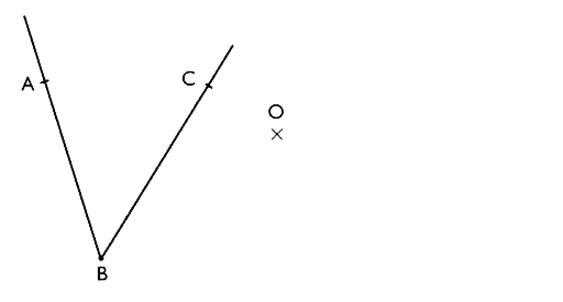
En utilisant une règle et un compas ,
construisez sur la figure 2 les points « E’ » , « F’ » ,
« G’ » symétriques par rapport à « I » des points « E’ » , « F » ,
« G ». |
|
|
|||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
Figure 3 : Image d’une figure dans une
symétrie centrale |
|
|
|||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
Voici un point « O » et une figure « F » .
La figure « F » est un ensemble de points. |
|
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
L’image de « F » dans la
symétrie centrale de centre
« O » est la figure
« F’ » constituée par l’ensemble des points qui sont les
symétriques des points de « F ». |
|
||||||||||||||||||||||
|
|
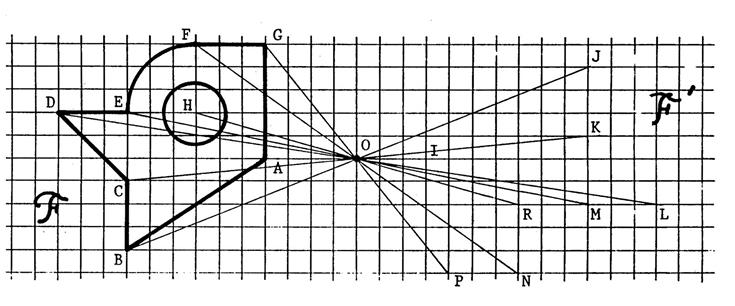
Sur le dessin ci-dessous ,
on a choisi quel que points de « F »et on a déterminé leurs images . En imaginant que l’on
fait la même chose pour tous les points de « F », complétez la
figure « F’ » . |
|
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
D’après ce que nous avons vu dans la fiche 1 , on peut dire |
|
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
Dans toute symétrie centrale ,
toute figure et son image sont superposables. |
|
|
||||||||||||||||||||
|
|
Dans toute symétrie centrale ,
la figure et son image ont donc même forme et mêmes dimensions . C’est ce que nous allons préciser pour les
figures élémentaires. ( il faut voir le dessin ci-dessus ) |
|
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
Segment : Le segment Ces segments ont même ..longueur…. et apparemment ils ont des supports identiques. Il en est de même pour le segment |
|
||||||||||||||||||||||
|
|
Droite :
l’image d’une droite est une ..droite…… |
|
||||||||||||||||||||||
|
|
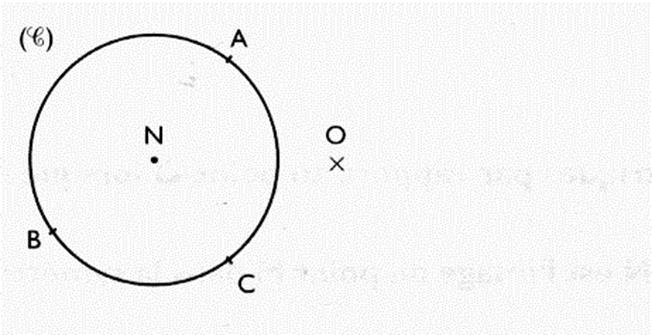
Cercle : Le cercle de centre « H »
a pour image le
cercle de centre « H’ ». Ces deux cercles ont le même ..diamètre…… Le centre de ces cercles sont …symétriques….par rapport à « O ». |
|
||||||||||||||||||||||
|
|
Angle : L’angle Il en est de même pour l’angle L’angle droit |
|
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
Fiche 4 : Construction de l’image d’une
figure. |
|
|
|||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
Activité 1 : |
|
||||||||||||||||||||||
|
|
En utilisant le quadrillage ,
( mais pas le calque ) |
|
||||||||||||||||||||||
|
|
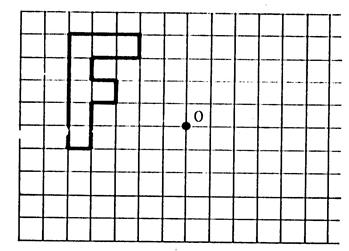
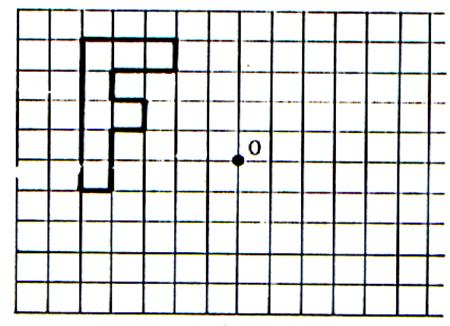
-
Dessinez ,
ci-dessous , l’image de la lettre « F » dans la symétrie
centrale de centre « O ». |
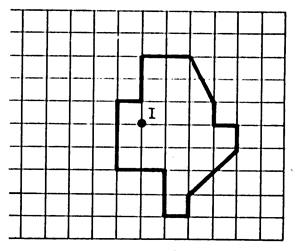
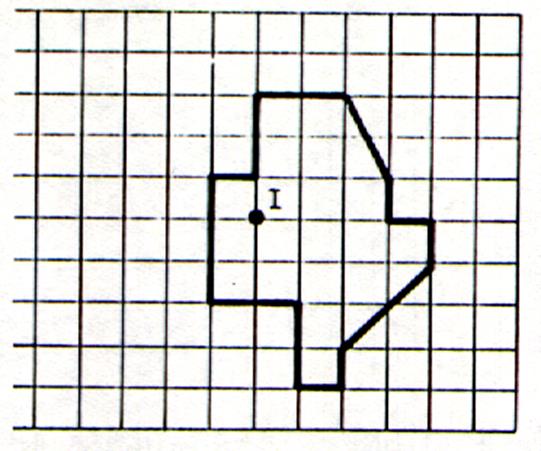
-
Dessinez la figure
ci-dessous dans la symétrie
centrale de centre « I ». |
|
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
Activité 2 : |
|
||||||||||||||||||||||
|
|
Dessinez avec la règle et le compas les deux
figures ci-dessous. |
|
|
|||||||||||||||||||||
|
|
Figure 1 : symétrie de centre
« E » |
Figure 1 : symétrie de centre
« S » |
|
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
Fiche 5 : Ne pas confondre « symétrie
centrale » et « symétrie
orthogonale » |
|
|
|||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
« symétrie centrale » |
« symétrie orthogonale » |
|
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
Activité : |
|
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
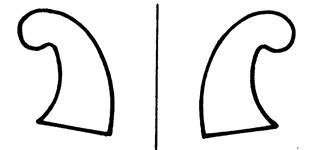
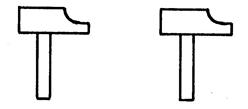
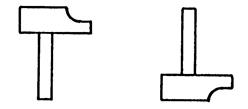
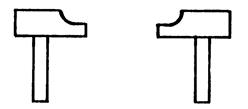
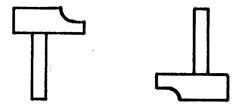
Dans chacun des
4 cas ci-dessous, vous allez chercher si les deux marteaux se
correspondent « oui » ou « non »dans une symétrie ( centrale ou orthogonale). Répondez en écrivant : « symétrie
centrale » ou « symétrie
orthogonale » ou « pas de
symétrie ». Dans le cas de symétrie centrale, placez le
centre de symétrie. Dans le cas de symétrie orthogonale
, placez l’axe de symétrie. |
|
||||||||||||||||||||||
|
|
Cas 1 |
Cas 2 |
|
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
Cas 3 |
Cas 4 |
|
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
Exercice N°2
|
En
utilisant le quadrillage , dessiner l’image de la
figure ci contre et reproduire son image dans la symétrie centrale de centre I. |
|
|
|
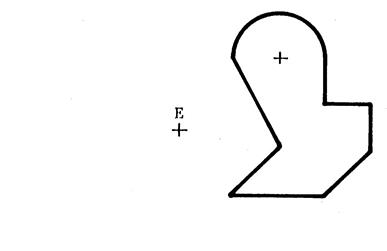
Exercice N°3
|
Dessiner avec la
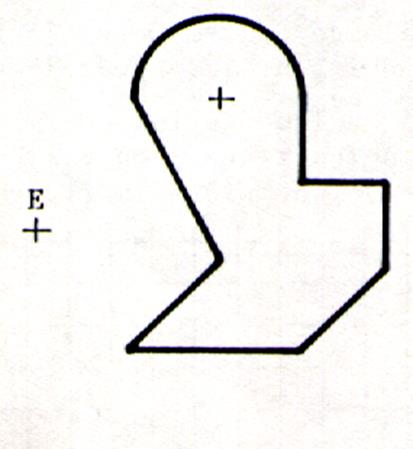
règle et le compas la symétrie de la figure ci-contre de centre E |
|
|
|
|
|
|
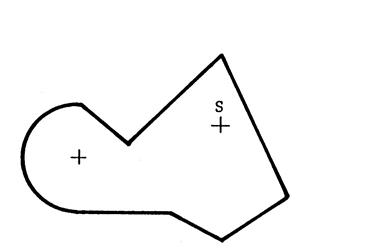
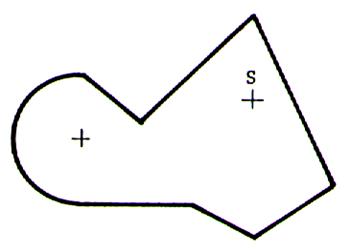
Exercice
N°4 |
Dessiner avec la
règle et le compas la symétrie de la figure ci-contre de centre S |
|
|
|
|
|