Milieu
- Définitions
- Milieu d'un segment
- Construction du milieu d'un segment
- Notes sur segment et paire.
Ces deux
mots, milieu et centre sont souvent confondus.
Le mot
"milieu" est utilisé lorsque l'on parle de segment ou de paire de
points.
Le mot
"centre" est utilisé lorsque l'on parle de cercle ou de
l'intersection de certaines droites
particulières d'un triangle ou de
l'intersection des diagonales d'un parallélogramme ou encore de symétrie centrale.
Le milieu
d'un segment est un point de ce segment situé à égale distance ( équidistant
de) de ses extrémités:
SI M est
le milieu de [AB]
ALORS AM
= MB et les
points A, M et B sont alignés.
L'idée de
milieu est intimement liée à l'idée d'alignement de points.
Le
théorème réciproque est vrai ( à condition de ne pas oublier le fait que les 3
points sont alignés, chose qui arrive souvent dans les démonstrations...): ce
qui est écrit ci-dessus en rouge l'est maintenant en vert après le
"SI" et ce qui était écrit en vert l'est en rouge après le
"ALORS". Cette réciproque est un bon outil pour prouver qu'un point
est le milieu d'un segment( ou d'une paire de points).
Remarquez
bien les différences de notations: AM est la notation utilisée pour une distance, c'est à dire un nombre, alors que [AB] est une notation
qui désigne une infinité de points alignés.
Construction du milieu d'un
segment :
Pour
construire le milieu d'un segment, vous pouvez utiliser l'une des méthodes
suivantes:
- Mesurer avec un double
décimètre la longueur du segment, diviser par 2 ce nombre. Le nombre
obtenu est la distance du milieu du segment à ses extrémités. C'est la
méthode la plus utilisée mais la moins conseillée par manque de précision.
- Tracer la médiatrice du segment. Cette médiatrice est une droite qui coupe
le segment en son milieu. Pointer l'intersection de cette droite avec le
segment et gommer cette droite si elle n'est pas utile par la suite ou si
elle encombre la figure.
[AB] ou {A,B} ? 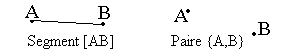
1. Un segment contient une infinité de
points alignés. Il a deux extrémités A et B. L'écriture des crochets a son
importance:
· ]A ou B[
signifient que l'extrémité A ou B n'appartient pas au segment. Dans ce cas on
dit que le segment est ouvert en cette extrémité: ]AB] segment ouvert en A ou
[AB[ segment ouvert en B. Le segment peut bien sûr être ouvert en ses deux
extrémités: ]AB[. Dans ce cas on dit que le segment est ouvert, sans préciser.
· [A ou B]
signifient que l'extrémité A ou B appartient pas segment. Dans ce cas on dit
que le segment est fermé en cette extrémité. Le segment peut bien sûr être
fermé en ses deux extrémités. Dans ce cas on ne précise rien: on dit "le
segment [AB]". C'est le cas qui est essentiellement étudié en 4ème de
collège.
· - cette
utilisation des crochets se retrouve en algèbre lorsque l'on désire représenter
une double inégalité, par exemple:
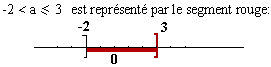
Le milieu d'un
segment fait donc partie des points de ce segment. Ce n'est qu'un point
particulier important de ce segment.
2. Le point C appartient au
segment [AB] lorsque AC + CB = AB. Si AC + CB est supérieure à AB alors le
point C est extérieur au segment [AB]. Il s'agit d'une propriété importante des
distances (inégalité triangulaire)
3.Une paire de points ne
contient que deux points et est notée par {A, B} (avec deux accolades) qui se
lit: paire AB. Le milieu d'une paire de points n'est donc pas contenu dans
cette paire. Pour le placer exactement sur une figure, il suffit de tracer tous
les points alignés entre A et B (avec une règle bien sûr), de placer le milieu
comme pour un segment et de gommer ce qui est inutile.