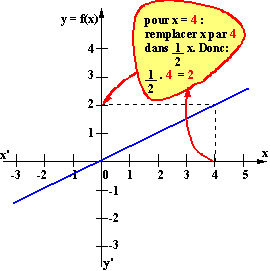|
WARMATHS |
Les Fonctions (généralités) |
|
|
Chapitres : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() Voir aussi: repères , fonctions linéaires , fonctions
affines , proportionnalité .
Voir aussi: repères , fonctions linéaires , fonctions
affines , proportionnalité .
** Une variable peut prendre
toutes les valeurs d'un ensemble d'objets donné. Dans l'ensemble des nombres
décimaux, l'expression numérique A = 2x²-1 la lettre x représente n'importe
quel nombre décimal. Cette expression peut être notée A = 2y²-1, dans ce cas la
variable est y...
A
la valeur choisie pour x correspond alors une valeur de l'expression A. Par
exemple pour x=3, A = 2*3²-1 et A = 17. Si nous changeons la valeur de
x, alors nous avons de fortes chances d'obtenir une autre valeur de A. par
exemple pour x = -2 nous obtenons A = 2*(-2)²-1 = 7.
![]() - Dans notre exemple, si nous choisissons x =
-3 alors :
- Dans notre exemple, si nous choisissons x =
-3 alors :
![]() A
= 2*(-3)² - 1=17...
A
= 2*(-3)² - 1=17...
Ce qui prouve que, bien que x varie, une expression peut prendre la même valeur
plusieurs fois.
![]() -
D'autre part, pour certaines expressions et pour certaines valeurs de la
variable, il est possible que nous n'obtenions pas de valeur.
-
D'autre part, pour certaines expressions et pour certaines valeurs de la
variable, il est possible que nous n'obtenions pas de valeur.
![]() Exemple:
Exemple:
pour B=1/(x-1), si x=1 alors B n'a pas de valeur car B=1/(1-1)
et B=1/0 ce qui n'est pas possible (division par zéro interdite).
** Une constante est une valeur qui reste toujours
la même, qui ne varie pas dès qu'elle est fixée. Dans l'expression C = 2(x-a) où x est la variable, nous devons définir une
fois pour toute la valeur de la constante a. Une fois cette valeur
définie, nous ne pouvons plus la modifier, sinon nous changeons d'expression:
pour a=1, a=-5 nous obtenons les expressions 2(x-1) et 2(x+5).
![]() Le choix du nom de la variable ou de la
constante, est soit imposé par l'énoncé du problème, soit par vous. Les
symboles choisis pour les représenter peuvent être des caractères de notre
alphabet (minuscules ou majuscules), des caractères grecs (tels que a, b, m, p,... ) ou d'autres signes encore.
Le choix du nom de la variable ou de la
constante, est soit imposé par l'énoncé du problème, soit par vous. Les
symboles choisis pour les représenter peuvent être des caractères de notre
alphabet (minuscules ou majuscules), des caractères grecs (tels que a, b, m, p,... ) ou d'autres signes encore.
II Qu'est
ce qu'une fonction ?
Une fonction est une relation
entre un ensemble d'objets de départ et un ensemble d'objets d'arrivée,
qui, à tout élément de l'ensemble de départ associe au plus un
élément de l'ensemble d'arrivée.
Le "au
plus" de la définition ci dessus signifie qu'un objet x du
départ est:
·
soit en relation avec un seul objet de
l'arrivée.
·
soit en relation avec aucun objet de l'arrivée.
Ces objets peuvent être des points, des nombres,..
Les ensembles de départ et d'arrivée peuvent être le même ensemble d'objets ou
des ensembles d'objets différents.
Par exemple, nous pouvons mettre en relation tous les points d'un
plan avec les points du même plan. C'est ce qui se passe lorsque nous
parlons de translation plane, de symétrie, de rotation : à tout point d'un plan
nous associons un point de ce plan en respectant certaines conditions. Le point
de départ est appelé antécédent et le point
d'arrivée est appelé image. Nous disons que l'image est fonction de
l'antécédent, ce qui signifie que le point image dépend du point
antécédent. Ce n'est qu'une question de vocabulaire...
|
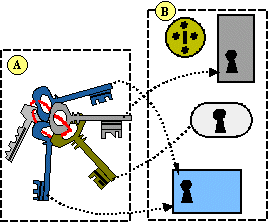
Un
autre exemple va vous montrer que les fonctions sont très courantes dans
notre quotidien. Il y a sûrement plusieurs serrures dans votre
habitation, pour lesquelles vous possédez un trousseau de clés. Chaque
clé est en relation avec au plus une serrure. Vous
ne pourrez ouvrir (ou fermer) telle ou telle serrure que si elle est fonction
d'au moins une clé de votre
trousseau... Nous considérons ici que l'ensemble de départ est le trousseau
de clés, l'ensemble d'arrivée étant l'ensemble des serrures de votre
habitation. Ces deux ensembles sont, cette fois, différents. |
|
![]() Remarque:
L'une des clés n'ouvre aucune serrure alors que deux clés ouvrent la même serrure
(c'est ce que signifie "fonction d' au moins une clé ")mais aucune clé (pas de "passe-partout"...)
n'ouvre plusieurs serrures. D'autre part il peut arriver qu'une ou plusieurs
serrures ne puissent être ouverte (ou fermée) avec l'une des clés du trousseau.
Remarque:
L'une des clés n'ouvre aucune serrure alors que deux clés ouvrent la même serrure
(c'est ce que signifie "fonction d' au moins une clé ")mais aucune clé (pas de "passe-partout"...)
n'ouvre plusieurs serrures. D'autre part il peut arriver qu'une ou plusieurs
serrures ne puissent être ouverte (ou fermée) avec l'une des clés du trousseau.
Lorsque
les ensembles de départ et d'arrivée sont finis (c'est à dire qu'ils comportent
un nombre connu d'éléments) nous pouvons les représenter graphiquement à l'aide
de flèches (représentation sagittale). Par exemples:
|
|
|
|
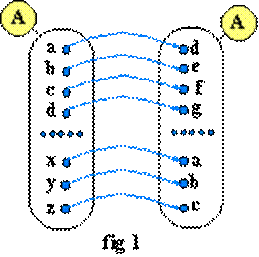
- La fig. 1 représente le même
ensemble deux fois: il s'agit de la représentation d'une fonction dans un
ensemble (le départ est aussi l'arrivée) : celui des caractères minuscules de
l'alphabet. L'image de a est d, celle de b est e,etc.
Cette fonction est une façon simple de coder un message (le rendre
incompréhensible pour un lecteur non averti). Le mot 'fonction'
serait codé 'irqfwlrq' (il suffit de
"sauter" les deux lettres qui suivent celle que l'on veut coder: n
o p q , donc n est codé avec la lettre q.
![]() Remarque:
nous pouvons ne dessiner qu'un seul ensemble A, mais dans ce cas le dessin est
moins lisible.
Remarque:
nous pouvons ne dessiner qu'un seul ensemble A, mais dans ce cas le dessin est
moins lisible.
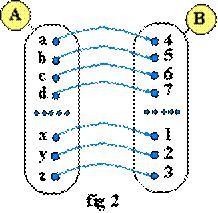
- La fig. 2 représente une fonction qui fait le même travail, mais au
lieu de coder avec des lettres, nous codons avec des nombres. L'ensemble
de départ est l'alphabet des minuscules, celui d'arrivée les nombres entiers de
1 à 26 (il y a 26 lettres dans l'alphabet). Chaque entier est le rang de la
lettre de code. Par exemple,l'image de a est 4, rang
de d. Le mot 'fonction' serait codé '9 18 17 6 25 12 18 17' (les
espaces entre chaque nombre sont nécessaires). Cette fois les deux ensembles
sont différents.
![]() Notez que dans ces exemples, chaque élément de
l'ensemble de départ a une image, et chaque élément de
l'ensemble d'arrivée a un antécédent. Ce qui n'est pas toujours le cas.
Notez que dans ces exemples, chaque élément de
l'ensemble de départ a une image, et chaque élément de
l'ensemble d'arrivée a un antécédent. Ce qui n'est pas toujours le cas.
Pour simplifier les écritures, nous
utilisons ce que nous appelons la notation fonctionnelle. Elle consiste à:
![]() -
donner un nom à la fonction: par exemple f, g, t,...
-
donner un nom à la fonction: par exemple f, g, t,...
![]() -
choisir un ensemble de départ et un ensemble d'arrivée.
-
choisir un ensemble de départ et un ensemble d'arrivée.
![]() -
mettre en relation un élément quelconque x (qui est donc une variable) de
l'ensemble de départ avec un élément y de l'ensemble d'arrivée.
-
mettre en relation un élément quelconque x (qui est donc une variable) de
l'ensemble de départ avec un élément y de l'ensemble d'arrivée.
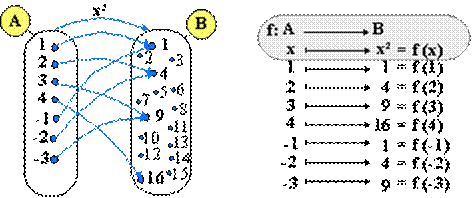
Par
exemple, nous pouvons décider que f désignera le fait que tout nombre x de
l'ensemble A = {1,2,3,4,-1,-2,-3}a pour image y=x² dans l'ensemble
B={1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16}. C'est à dire qu'à chaque
nombre x de A on associe le nombre y de B qui est égal au carré de x. Ce qui
est représenté sur la figure suivante:
|
|
Dans le cadre ![]() la
première ligne indique les ensembles concernés, ainsi que le sens d'application
(de A vers B) de la fonction de nom f. La seconde ligne expose comment obtenir
l'image y dans B, d'un élément x de A. Nous pouvons noter que y=x²=f(x) ou
y=f(x).
la
première ligne indique les ensembles concernés, ainsi que le sens d'application
(de A vers B) de la fonction de nom f. La seconde ligne expose comment obtenir
l'image y dans B, d'un élément x de A. Nous pouvons noter que y=x²=f(x) ou
y=f(x).
Dans les
calculs, par commodités, la notation f(x) = x² ou y=x² est très souvent
utilisée. Elle se lit "f de x égale x²" et signifie que l'image
de x par f est x² (ou y).
![]() Dans cet exemple, x² est l'image de x. Autrement
dit: x est l'antécédent de x².. Vous pouvez remarquer
qu'un élément de B (ensemble d'arrivée) peut avoir plusieurs antécédents (nous
sommes dans le cas où "plusieurs clés peuvent ouvrir la même serrure"
voir plus haut)
Dans cet exemple, x² est l'image de x. Autrement
dit: x est l'antécédent de x².. Vous pouvez remarquer
qu'un élément de B (ensemble d'arrivée) peut avoir plusieurs antécédents (nous
sommes dans le cas où "plusieurs clés peuvent ouvrir la même serrure"
voir plus haut)
V Variation
d'une fonction numérique:
![]() Une fonction est dite numérique lorsque les
ensembles de départ et d'arrivée sont des ensembles de nombres.
Une fonction est dite numérique lorsque les
ensembles de départ et d'arrivée sont des ensembles de nombres.
Si nous chauffons une tige de métal, sa longueur augmente avec sa
température: la longueur est fonction de la température. Lorsque la température
augmente, la longueur de la tige augmente (et lorsque la température diminue,
la longueur diminue) : cette fonction est croissante.
Soit une corde d'un cercle. La longueur de cette corde augmente lorsque sa
distance au centre du cercle diminue et la longueur de la corde diminue lorsque
sa distance au centre augmente : cette fonction est décroissante.
![]() Une fonction f est croissante lorsque x
et f(x) varient dans le même sens.
Une fonction f est croissante lorsque x
et f(x) varient dans le même sens.
Une fonction f est décroissante lorsque x et f(x) varient en sens contraire.
Lorsque
la valeur de la variable x passe de la valeur initiale x1 à la
valeur finale x2, l'accroissement de la variable x est x2-x1
(valeur finale moins valeur initiale) et la valeur de f(x) passe de f(x1)
à f(x2) ce qui correspond à un accroissement de la fonction de f(x2)-f(x1).
Croissance d'une fonction:
Si nous choisissons x2 plus grand que x1
alors l'accroissement x2-x1 de la variable est positif.
Dans ce cas si f(x2)>f(x1)
alors f(x2)-f(x1) est aussi positif alors
la fonction considérée est croissante car les accroissements de x et f(x) sont
de même signe (une augmentation correspond à une augmentation). Si f(x2)<f(x1) alors f(x2)-f(x1)
est négatif : la fonction est décroissante (à une augmentation
correspond une diminution).
Les résultats sont similaires si nous choisissons x2
plus petit que x1 : alors x2-x1 est
négatif.
Dans ce cas si f(x2
)>f(x1 ) alors f(x2 )-f(x1 )
est positif : la fonction considérée est décroissante. Si f(x2 )<f(x1 ) alors f(x2 )-f(x1
) est négatif : la fonction considérée est croissante.
![]() Considérons
le signe du rapport:
Considérons
le signe du rapport: ![]() .
Si ce rapport est positif alors la fonction est croissante (le
numérateur et le dénominateur sont de même signe), sinon elle est
décroissante.
.
Si ce rapport est positif alors la fonction est croissante (le
numérateur et le dénominateur sont de même signe), sinon elle est
décroissante.
Récapitulons:
|
Fonction croissante |
Fonction décroissante |
|
x2
>x1 et f(x2) >
f(x1) ou x2 - x1 et f(x2) - f(x1)
positifs x2
< x1 et f(x2) < f(x1) ou x2 -x1 et f(x2) -
f(x1) négatifs
|
x2>x1 et f(x2)< f(x1) ou x2>x1 et f(x2) <
f(x1) soit
: x2 - x1 et f(x2) - f(x1) de signes différents
|
1. Fonctions géométriques:
- Dans
le plan : les ensembles de départ et d'arrivée sont les mêmes; il s'agit
d'ensembles de points. Nous en connaissons quelques unes: les symétries centrales et orthogonales, les translations. Nous les avons appelées transformations dans
le plan.
- Dans
l'espace : nous pouvons définir des symétries, des translations,...
mais cette fois les ensembles de départ sont l'espace. Ces notions dépassent
largement les programmes de géométrie du collège. Cependant, nous donnerons ici
un exemple concernant l'établissement d'une carte du globe terrestre.
Une carte terrestre est un morceau de plan (rectangulaire le plus souvent) alors
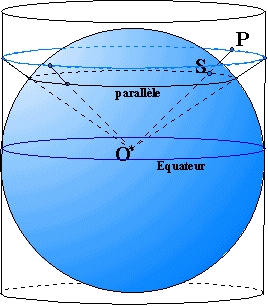
que le globe terrestre peut être assimilé à une sphère. Nous allons
établir une relation entre les points d'une sphère et les points d'un plan de
la manière suivante :
|
|
Une sphère de centre O est placé dans un cylindre de même diamètre. L'image d'un point S de la sphère
est le point P de la face latérale du cylindre, obtenu par l'intersection de
la demi droite [OS) avec la face latérale du cylindre. Le point S est sur
le parallèle, son image P est sur la face latérale du cylindre. Lorsque
le point S parcourt le parallèle, son image P parcourt le cercle bleu tracé sur
cette face du cylindre.
|
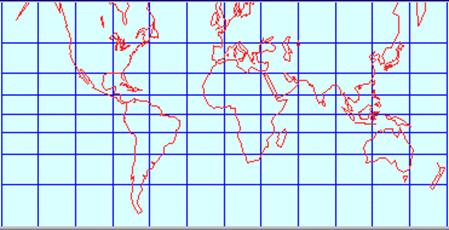
Après
découpage et "mise à plat" de la face latérale du cylindre, le cercle
bleu sur la face latérale du cylindre devient une droite sur le plan de la
carte (figure ci dessus à droite). Il s'agit d'une projection cylindrique peu
utilisée en cartographie car elle déforme beaucoup et de plus en plus après les
parallèles de 40° Nord(représenté sur la figure par un
petit "cercle" noir) et Sud.
2. Fonctions numériques:
Les
ensembles de départ et d'arrivée sont des ensembles de nombres (entiers
naturels ou relatifs, décimaux, rationnels, réels...).
Il est souvent impossible de représenter les ensembles de départ et d'arrivée
comme au II et au
III : les ensembles de nombres contiennent souvent
une infinité d'éléments. C'est le cas dans les exemples suivants. Nous
utilisons alors un système d'axes gradués: voir le document sur les
repères
Exemple 1:
![]() ensemble de départ : ensemble des nombres réels
ensemble de départ : ensemble des nombres réels
![]() ensemble
d'arrivée : ensemble des nombres réels
ensemble
d'arrivée : ensemble des nombres réels
La fonction est:
![]()
|
Il
s'agit d'une fonction linéaire. Ce type de fonction représente une proportionnalité, le
coefficient (1/2 dans notre exemple) est un coefficient de proportionnalité.
Pour plus d'infos sur les proportionnalités, voir le Répertoire. |
|
Exemple
2:
![]() ensemble de départ : ensemble des nombres réels
ensemble de départ : ensemble des nombres réels
![]() ensemble
d'arrivée : ensemble des nombres réels
ensemble
d'arrivée : ensemble des nombres réels
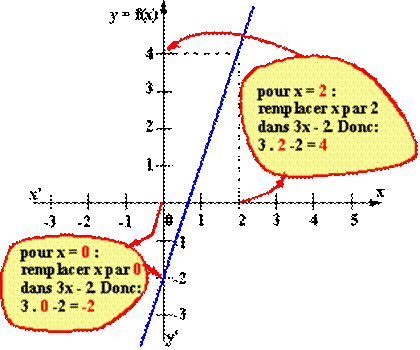
![]() La
fonction est:
La
fonction est: ![]()
Il s'agit d'une fonction affine. Il nous faut calculer la position de deux
points de la droite représentative. Voir aussi le document sur les fonctions affines.
![]() Exemple 3 :
Exemple 3 :
ensemble de départ : les nombres
réels de 0 à 90.
ensemble d'arrivée : les nombres réels de
0 à 1.
La fonction est:
![]() .
.
Nous utilisons ici un
repère orthogonal gradué pour les abscisses, en
degrés (1cm pour 10 degrés) et pour les ordonnées, les valeurs du cosinus (4cm
pour 1):
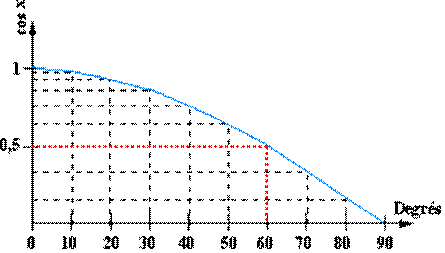
![]() Le
cosinus de 60° (cos 60) est égal à 0,5 : ce qui est représenté par les lignes
en pointillés rouges.
Le
cosinus de 60° (cos 60) est égal à 0,5 : ce qui est représenté par les lignes
en pointillés rouges.