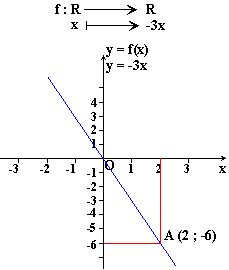WARMATHS

Les fonctions linéaires

· Définition

· Représentation graphique

· Propriétés:

o Fonctions croissantes, décroissantes

o Coefficient directeur

o Cas particuliers

· Calculs pratiques

Voir aussi: repères , fonctions(généralités), fonctions affines , proportionnalité .

L'ensemble de tous les nombres (nombres réels) est noté R, celui des nombres décimaux D, celui des entiers naturels N et celui des entiers relatifs Z.

I Définition:

Si, à tout nombre x appartenant à R, nous associons le nombre ax alors nous avons défini la fonction linéaire de coefficient a.
Comme pour toute fonction (voir le document sur les fonctions), si nous appelons cette fonction f, nous noterons:

ax est l'image de x. Avec la notation fonctionnelle: f(x) = ax.

Dans ax, la variable est x alors que a est un nombre constant.
Une fonction linéaire représente une situation de proportionnalité. Son coefficient est le coefficient de proportionnalité de cette situation. Voir le document sur les proportionnalités.

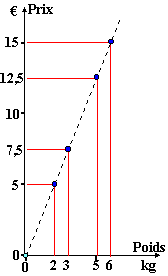
Exemple: si vous achetez des fruits au poids à 2,5 € le kilogramme, la variable est le nombre de kilogrammes que vous achetez, alors que la constante est le prix au kilogramme. Le tableau ci-dessous exprime cela:

	2 kg	3kg	5kg	6kg	0kg	variable
	5 €	7,5 €	12,5 €	15 €	0 €	image

Il s'agit d'une situation de proportionnalité: le prix est proportionnel au poids. Le coefficient de proportionnalité est 2,5 (c'est le prix au kilogramme).

Nous pouvons utiliser cette situation pour définir la fonction linéaire associée: appelons la g:

où p est le poids de fruits achetés et 2,5 le coefficient de la fonction linéaire.

Comme R désigne l'ensemble de tous les nombres, y compris les nombres négatifs, la situation de proportionnalité qui a servi de modèle, ne représente (5 points) qu'une partie de la fonction linéaire associée. Nous observons que ces 5 points sont alignés sur une droite (en pointillés) passant par l'origine du repère.

II Représentation graphique:

Nous utiliserons ici des repères orthogonaux normés ou non (voir le document sur les repères).
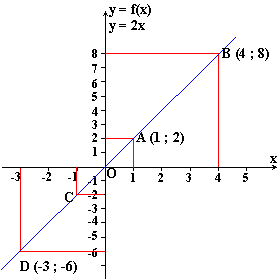
Soit f la fonction linéaire qui associe à x le nombre 2x. C'est à dire:

Dans le tableau suivant nous calculons les images de diverses valeurs prises par la variable x et nous plaçons les points représentatifs dans un repère orthogonal (non normé : les graduations sont différentes sur les deux axes):

Valeurs prises par x	Images de ces valeurs	Coordonnées du point associé
x	2 fois x	P (x ; 2x)
1	2 fois 1 = 2	A (1 ; 2)
4	2 fois 4 = 8	B (2 ; 8)
0	2 fois 0 = 0	O (0 ; 0)
-1	2 fois -1 = -2	C (-1 ; -2)
-3	2 fois -3 = -6	D ( -3 ; -6)

Nous observons encore que ces points sont alignés sur la droite (OA). La droite (OA) est appelée droite représentative de la fonction linéaire f et nous dirons que la droite (OA) a pour équation y = 2x .

Nous pouvons démontrer la propriété suivante (voir la démonstration) :

La courbe représentative d'une fonction linéaire est une droite passant par l'origine du repère.

Toute droite, différente de l'axe des ordonnées, passant par l'origine du repère représente une fonction linéaire.
Pour représenter une fonction linéaire il suffit de calculer les coordonnées d'un seul point. La droite qui passe par ce point et par l'origine du repère est la droite représentative. Par exemple: représenter dans un repère d'origine O, la fonction linéaire f(x) = 5 x. Pour x= 1 nous avons y=f(1)=5×1, soit y=5. Le point A(1;5) est sur la droite représentative de f. La droite (OA) est cette droite représentative.

I Propriétés:

1. Fonctions croissantes, décroissantes:

Soient les fonctions linéaires f(x)=2x.
Les valeurs x₁ et x₂ de x telles que x₁< x₂ (-1 et 2 par exemple) ont pour images f(x₁)=2x₁ et f(x₂)=2x₂ (dans l'exemple: f(-1)=-2 et f(2)=4). Comme x₁< x₂ alors x₂- x₁ est positif (dans l'exemple: 2- (-1)=3). Pour leurs images : f(x₂)- f(x₁)=2x₂ - 2x₁=2(x₂- x₁) (dans l'exemple: et f(2)-f(-1)=4-(-2)=6). Comme x₂- x₁ est positif alors f(x₂)- f(x₁) est aussi positif. Ce qui démontre que f est croissante (voir le document sur les fonctions).

Soit maintenant la fonction linéaire g(x)= -2x. Pour les mêmes valeurs x₁ et x₂ nous avons g(x₂)- g(x₁)=-2x₂ - (-2x₁)=2(x₁- x₂). Comme x₁- x₂ est négatif (c'est l'opposé de x₂- x₁) alors g(x₂)- g(x₁) est négatif. Cette fois la fonction linéaire g est décroissante.

Conclusion: nous admettrons qu'une fonction linéaire f(x)=ax est croissante lorsque a est positif, décroissante lorsque a est négatif.

Pour les curieux : voir une démonstration plus générale.

2. Coefficient directeur:

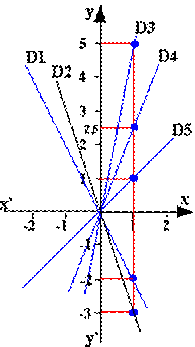
Sur la figure ci-contre, toutes les droites passent par l'origine du repère. Elles représentent autant de fonctions linéaires. Pour déterminer leur coefficient a il suffit d'avoir les coordonnées d'un point sur la droite.
Pour D1 le point bleu a pour coordonnées (1 ; -2). C'est à dire que l'image de 1 par la fonction linéaire représentée par D1 est -2. Donc -2=a.1 d'où a = -2. Remarquons que D1 représente alors une fonction linéaire décroissante (d'après ce qui a été exposé au 1° ci dessus) et que D1 passe dans les quadrants II et IV.

Pour D2 l'image de 1 est -3. Donc -3=a.1 et a = -3. D2 représente, comme D1, une fonction linéaire décroissante. Et D2 va du quadrant I dans le quadrant II (ou vice versa).

Pour D3, nous avons 5 = a.1 et a =5. La droite D3 représente donc une fonction linéaire croissante. D3 va du quadrant III dans le quadrant I.

De même pour les droites D4 et D5 nous calculons respectivement les coefficients a. Nous trouvons 2,5 et 1. Chacune de ces droites représente une fonction linéaire croissante : elles vont du quadrant III dans le quadrant I (et vice versa).

Le coefficient a indique donc le type de fonction linéaire (croissante ou décroissante) ainsi que le type de droite représentative. Nous appellerons le coefficient a coefficient directeur de la fonction linéaire(pour faire référence à la direction suivie par la droite représentative.

Récapitulation: pour la fonction linéaire f(x)=ax
Si a est positif, f est croissante.
Si a est négatif, f est décroissante.

2. Cas particuliers:
Soit la fonction linéaire f(x)=ax. Si a=0 alors f(x)=0 quelque soit la valeur donnée à x.
La fonction f(x)=0 est la fonction linéaire constante. Sa représentation est la droite supportant l'axe des abscisses (fig 1). En effet, toutes les valeurs de x sont représentées par les point de l'axe des abscisses et leur image est toujours 0. La droite représentative, dans ce cas, contient les points de coordonnées (x;0) qui se trouvent sur l'axe des abscisses.

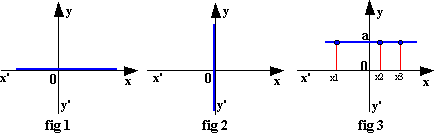
Remarques:

- La droite supportant l'axe des ordonnées représente la fonction x=0 (tous les points de l'axe des ordonnées ont pour coordonnées (0, y) (fig 2). Ce n'est pas la représentation d'une fonction linéaire puisqu'une seule valeur de x est représentée.
- La droite représentant la fonction f(x)=a est une droite parallèle à l'axe des abscisses et passant par le point de coordonnées (0;a) (fig 3). En effet, quelque soit la valeur donnée à x (x1, x2, x3,...etc.), l'image est a. Cette fonction n'est pas une fonction linéaire puisque sa représentation ne passe pas par le point origine du repère.

III Calculs pratiques:

· Calculer une image.

· Calculer un antécédent.

· Définir une fonction linéaire connaissant un nombre et son image.

· Représenter graphiquement une fonction linéaire donnée

· Utiliser une représentation graphique pour:

o Lire une image.

o Lire un antécédent.

o Lire les coordonnées d'un point de la droite représentative.

o Définir la fonction linéaire représentée.

1. Calcul de l'image d'un nombre:
Soit la fonction linéaire f(x)=4x.
Calculer l'image de 3, par exemple, c'est remplacer x par 3 dans la définition de la fonction : f(3)=4×3=12.
L'image de 3 par f est donc 12.

2. Calculer l'antécédent d'un nombre à partir de son image:

C'est à dire : calculer le nombre qui a pour image un nombre connu.
Par exemple : soit f(x)= 4x et l'image de x est 12. Quelle est la valeur de l'antécédent x?
Comme l'image de x est f(x), nous avons f(x)=12 avec f(x)=4x (par définition de la fonction).
Nous pouvons donc écrire : 4x=12 d'où il vient x=12/4, soit x=3 (ce qui correspond bien aux données du 1. ci dessus.

3. Définir la fonction linéaire à partir d'un nombre et de son image:
Soit la fonction linéaire f. Nous savons que l'image de 5 est 20, c'est à dire f(5)=20.
Pour définir la fonction linéaire f, il suffit de calculer son coefficient directeur :

f(x)=ax
avec les données : f(5)=a×5 et f(5)=20
d'où a×5=20
et a=20/5 soit a=4

La fonction linéaire cherchée est donc : f(x)=4x (c'est à dire : l'image de x par f est 4x).
Remarque: vous pouvez remarquer que le coefficient directeur est le quotient de l'image 20 par l'antécédent 5 (c'est à dire 20/5). Il est donc très facile, en appliquant cette remarque, de calculer le coefficient directeur d'une fonction linéaire f. Voici quelques autres exemples:
L'image de 3 est 9 : le coefficient directeur est égal à 9/3=3 et la fonction linéaire est f(x)=3x.
L'image de 8 est 3 : le coefficient directeur est égal à 3/8 et la fonction linéaire est f(x)=(3/8)x ou f(x)=3x/8.
L'image de 4,5 est -1,5 : le coefficient directeur est égal à -1,5/4,5=-1/3 (après simplification). La fonction linéaire est f(x)=(-1/3)x ou f(x)=-x/3.

4. Représenter graphiquement une fonction linéaire :
Représenter dans un repère d'origine O et d'axes orthogonaux, la fonction linéaire f(x)= -3x.

Nous savons que la droite représentative d'une fonction linéaire passe toujours par l'origine du repère. Pour tracer cette droite il suffit d'en connaître deux points. Nous en avons déjà un : O. Il suffit donc de calculer les coordonnées d'un point A en choisissant une valeur de x. Par exemple x=2 . Le nombre 2 est alors l'abscisse de A et son ordonnée est f(2)= -3×2=-6. Nous n'avons plus qu'à placer dans le repère le point A(2;-6). La droite (OA) est la droite représentative de la fonction f(x)= -3x.

5. Utiliser la représentation graphique d'une fonction linéaire:
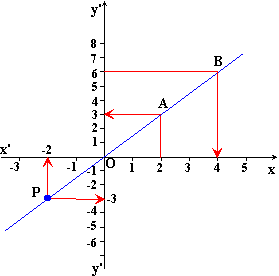
Dans le repère d'origine O et d'axes orthogonaux (x'x) et (y'y), la droite (D) représente la fonction linéaire f.

a. Lire l'image de 2:
Le nombre 2 est l'abscisse (sur l'axe (x'x)) d'un point de (D). Pour trouver ce point A il faut tracer une ligne de rappel parallèle à l'axe (y'y) (Attention: si le repère n'est pas orthogonal, cette ligne n'est pas perpendiculaire à (x'x), mais reste parallèle à (y'y)) et passant par le point d'abscisse 2 sur (x'x). Dès que ce point A est déterminé, il nous faut tracer la ligne de rappel qui passe par A et parallèle à (x'x). Cette ligne de rappel coupe l'axe (y'y) en un point dont l'ordonnée est l'image de 2 : f(2)=3.

b. Lire l'antécédent de 6:
Les valeurs des images se trouvent sur l'axe des ordonnées (y'y). Le nombre 6 est donc l'ordonnée d'un point de (D).

Pour trouver ce point B il faut tracer une ligne de rappel parallèle à l'axe (x'x) (Attention: si le repère n'est pas orthogonal, cette ligne n'est pas perpendiculaire à (y'y), mais reste parallèle à (x'x)) et passant par le point d'ordonnée 6 sur (y'y). Dès que ce point B est déterminé, il nous faut tracer la ligne de rappel qui passe par B et parallèle à (y'y). Cette ligne de rappel coupe l'axe (x'x) en un point dont l'abscisse est l'antécédent de 6 : f(4)=6
c. Lire les coordonnées d'un point de (D):
Lire les coordonnées du point P (voir figure ci dessus) c'est tracer les lignes de rappel passant par P Ces lignes coupent les axes en un point sur (x'x) dont l'abscisse est l'abscisse de P, et en un point de (y'y) dont l'ordonnée est l'ordonnée de P. Nous trouvons P(-2;-3).
d. Définir la fonction linéaire représentée par (D):
D'une façon générale, il nous faut les coordonnées d'un point de (D). Nous devons donc choisir un point sur (D) dont les coordonnées sont "lisibles", c'est à dire ne pas demander une trop grande précision de lecture par rapport aux graduations du repère (du type 2,1 par exemple, avec des axes gradués comme sur la figure ci dessus). L'idéal c'est de rechercher des coordonnées entières...
Pour cet exercice nous choisissons le point P(-2;-3) et nous appliquons la méthode donnée au 3.. Nous obtenons : f(x)=1,5x.