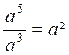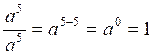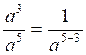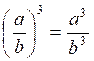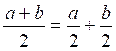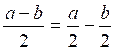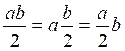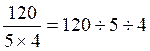|
|
|
DOC : Formation Individualisée |
DOC : Elève. |
|
i9 |
Le calcul numérique |
:i |
|
i9 |
Liste des objectifs
« passerelle » 3ème / Seconde. |
:i |
|
i9 |
:i |
|
ALGEBRE. N° 35 Formulaire |
Informations sur d’autres « TRAVAUX »
|
|
|
Formules
|
Traduction littérale |
|
|
a
+ (b + c)= a + b + c |
Pour
additionner une somme, on supprime les parenthèses. |
|
|
a
- (b + c)= a - b - c |
Pour
soustraire une somme, on en retranche successivement les termes. |
|
|
a
+ (b - c)= a + b - c |
Pour
ajouter une différence,on ajoute le premier terme et on retranche le
second. |
|
|
a
- (b - c)= a - b + c |
Pour
retrancher une différence,on retranche
le premier terme et on ajoute le second. |
|
|
a
+ (b + c - d) = a + b + c -d |
+
(+) =+ et - (-) = + |
|
|
a
- (b + c - d) = a - b - c -d |
-
(+) =
- et +
(-) = - |
|
|
4
(a + b) = 4a + 4b |
Pour
multiplier une somme par un nombre on multiplie chaque terme par ce nombre et on ajoute les
produits. |
|
|
4
(a - b) = 4a - 4b |
Pour
multiplier une différence par un nombre , on
multiplie chaque terme par ce nombre
et on retranche le second produit du
premier. |
|
|
a b + ac - ad = a (b + c - d) |
Une
expression algébrique contenant des produits ayant un facteur commun peut se
mettre sous la forme d’un produit de deux facteurs dont le premier est le
facteur commun et l’autre l’expression algébrique des facteurs qui
l’accompagnent. |
|
|
(a +b) (c +d)= ac + ad + b c + b d |
( -) ´ ( + ) = ( - ) ( +) ´ ( - ) = ( - ) ( -) ´ ( - ) = ( + ) ( +) ´ ( + ) = ( + ) |
|
|
(a +b) (c -d)= ac - ad + b c - b d |
|
|
|
(a - b)(c - d)= ac - ad - b c + b d |
|
|
(a
+ b) ² = a² + 2ab + b² |
Le
carré d’une somme est égal au carré du premier terme « + » le double produit du premier par le second
terme « + » le carré du second. |
|
|
(a
- b) ² = a² - 2ab + b² |
Le
carré d’une différence est égal au carré du premier terme « - » le double produit du premier par le second
terme « + » le carré du second. |
|
|
a² - b² = (a + b) ( a - b) |
La
différence des 2 carrés de 2 quantités est é gale au produit de leur somme
par leur différence. |
|
|
d (abc) = d abc |
Pour
multiplier un produit par un nombre, on l’introduit comme nouveau facteur. |
|
|
(a b) (d e c) = a b d e c |
Pour
multiplier un produit par un produit,
on fait le produit général de tous les facteurs. |
|
|
a3 ´
a² =
a 3+2 |
Produit
de deux puissances, on ajoute les exposants. |
|
|
(a 3)² = a 3´2 |
Puissances
de puissance : on multiplie les exposants. |
|
|
(a
b c) ² = a ² b² c² |
Puissance d’un produit : on élève
chaque facteur à la puissance donnée. |
|
|
|
Quotient
de puissance : on soustrait les puissance. |
|
|
|
Tout
nombre à la puissance « 0 » vaut l’unité (
=1) |
|
|
|
Si
l’exposant du dénominateur est plus fort, le quotient a pour
numérateur « 1 » et le dénominateur à pour puissance, la différence des puissances la plus
grande moins la plus petite. |
|
|
|
Puissance
d’un quotient : on élève chaque terme du quotient par la puissance
indiquée. |
|
|
|
Pour
diviser une somme par un nombre, on
divise chaque partie par ce nombre et on ajoute les deux quotients. |
|
|
|
Pour
diviser une différence par un nombre, on divise chaque partie par ce nombre
et on retranche le second quotient. |
|
|
|
Pour
diviser un produit par un nombre, on divise un des facteurs par ce nombre. |
|
|
|
Pour
diviser un nombre par un produit, on divise ce nombre par le premier, puis
par le second, etc. |