|
|
|
DOC : Formation Individualisée |
DOC : Elève. |
|
ALGEBRE. N° 20 |
Information
« TRAVAUX » |
|
OBJECTIFS :- médiation en algèbre. |
I ) Pré requis:
|
i9 |
Le calcul numérique |
:i |
|
i9 |
Liste des objectifs « passerelle »
3ème / Seconde. |
:i |
|
i9 |
:i |
II
)
ENVIRONNEMENT du dossier :
III )
LECON n°20 : PUISSANCE ALGEBRIQUE.
IV) INFORMATIONS
« formation leçon » :
|
|
Travaux auto - formation. |
|
Corrigé des travaux auto -
formation. |
|||
V )
DEVOIRS ( écrits):
|
Devoir diagnostique L tests. |
|
|
Devoir Auto - formatif (intégré au cours) |
|
|
Devoir Formatif « Contrôle :
savoir » ; (remédiation) |
|
|
|
|
|
Devoir sommatif. |
|
|
Devoir certificatif : (remédiation) |
|
* remédiation : ces
documents peuvent être réutilisés ( tout ou partie)
pour conclure une formation .
|
Leçon |
Titre |
|
N°20 |
PUISSANCE
ALGEBRIQUE |
Déjà
vu : 3´3 = 3² ; 3´3´3 = ![]()
|
PUISSANCE
ALGEBRIQUE |
|
I°)
Définition.
On
appelle « puissance d’un nombre » le produit de plusieurs facteurs
égaux à ce nombre.
a´a = a² ( lire “a”
carré ou « a » puissance « 2 » )
a´a´a = ![]() ( lire “a” au
cube ou « a » puissance « 3 » )
( lire “a” au
cube ou « a » puissance « 3 » )
a´a´a´a =![]() ( lire “a” puissance
« 4 » )
( lire “a” puissance
« 4 » )
2 ;
3 ; 4 s’appellent « exposants ».
II)
Produit de deux puissances d’un même
nombre.
(information complémentaire)
(a´a )( a´a´a) =
a´a´a ´a´a
= ![]()
= a² ´![]() =
= ![]()
on
retiendra :
Dans
le produit de deux puissances d’un même nombre on ajoute les exposants.
III)
Puissance de puissance.
(a²)3 = a ² ´ a² ´a² = a´a
´a ´a
´a
´a
= a2+2+2 = a 3´2
= a 6
on
retiendra :
Dans
une puissance de puissance d’un même nombre ou terme,on multiplie les exposants.
IV)
Puissance d’un produit.
(abc)² = abc ´ abc
= aabbcc
= a² b²
c²
On
retiendra :
Dans
la puissance d’un produit on élève chaque facteur à la puissance
indiquée.
V)
Quotient de puissances.
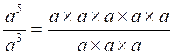
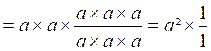
= a²
= a 5-3
On retiendra :
Dans le quotient d’un même nombre on
soustrait les exposants.
a
Remarques :
1°)
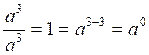
On retiendra que tout nombre muni d’un exposant « zéro » vaut
l’unité.
2°)
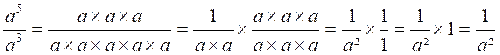
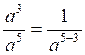
On retiendra que dans un quotient
quand le dénominateur a une puissance plus élevée que le numérateur
, le quotient est une fraction qui a pour numérateur l’unité et pour dénominateur la lettre affectée
d’un exposant égal à la différence des deux exposants donnés.
VI) Puissance d’un quotient.
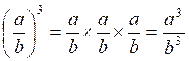
On retiendra : que dans une
puissance d’un quotient on élève chaque
terme du quotient à la puissance indiquée.
|
Titre |
|
|
N°20 |
TRAVAUX d’Auto -
FORMATION sur PUISSANCE
ALGEBRIQUE |
Compléter les phrases suivantes :
I Définition :
On appelle « puissance d’un
nombre » ………………………………………. à ce nombre.
II) Produit de deux puissances d’un même nombre
Dans le produit de deux puissances
d’un même nombre ………………. les exposants.
III) Puissance de puissance.
Dans
une puissance de puissance d’un même nombre ou terme,on ………………………………….
IV) Puissance d’un produit.
Dans la puissance d’un produit
on élève ……………………………………………..
V) Quotient de puissances.
Dans
le quotient d’un même nombre on ………………….. les
exposants.
Tout
nombre muni d’un exposant
« zéro » vaut …………….
Dans un quotient quand le dénominateur a une
puissance plus élevée que le numérateur , le quotient
est une …………………………………………………..
VI)
Puissance d’un quotient.
Dans une puissance d’un
quotient on élève chaque terme du
quotient …………………………..
1°)
Faire les exercices suivants :
I )
Définition :
a´a =
a´a´a =
a´a´a´a =
2 ; 3 ; 4
s’appellent
…………………...
II)
Produit de deux puissances d’un même
nombre. a² ´![]() =
=
III)
Puissance de puissance. (a²)3 =
IV)
Puissance d’un produit. (abc)² =
V)
Quotient de puissances. ![]()
Remarques :
1°)
![]()
2°)
![]()
VI) Puissance d’un quotient. 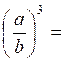
2°)
Effectuer (développer et réduire si possible) :´
|
1 |
(a´a) (a´a´a) |
|
A |
(cdb)² = |
|
=2 |
a3
´a5 |
B |
( 2 a b²c3)² |
|
|
3 |
(a3)3 |
C |
4
a 3 b3 c ´ 3abc2 |
|
|
4 |
(a6)2 |
D |
6ab²d
´ 4 cb² |
|
|
5 |
3x²y
´ 5 x y² |
E |
5
ab0d² ´ 6 a² b²c |
|
|
6 |
5xy ´ 10 x² y² |
F |
5x²
´ 3´² |
1°) Une personne
voulant faire une promenade prend
au départ une voiture qui fait 12 kilomètres à l’heure. A quelle
distance du point de départ devra- t- elle quitter la voiture pour que,
revenant à pied et faisant 4 kilomètres à l’heure, elle soit de retour 5 heures
après le départ.
CORRIGE :
1°) Effectuer
(développer et réduire si possible) :
|
1 |
(x+y) (4 + 3) |
|
A |
(x - 5)(y-7) |
|
2 |
(x + y) (5 - 3) |
B |
(3x+4)(3x-7) |
|
|
3 |
(x + 4) (y + 3) |
C |
(3- 2b)(5a-7) |
|
|
4 |
(x+5) (y - 3) |
D |
(3a+7)(2-3b) |
|
|
5 |
(x - 7) (y + 5) |
E |
(3x-3)(5-4y) |
Problèmes :
1°).
Un train de marchandise est parti de Sedan pour se rendre à Charleville à 8
heures du matin et sa vitesse moyenne est de 36 kilomètres à l’heure. Le « T. E. R. » est parti à 8 h.1/2 de la même destination avec une
moyenne de 42 kilomètres à l’heure, il est arrivé à Charleville 1/4 d’heure après le train de marchandise.
Quelle est la distance de Sedan à Charleville ?