|
Auteur :
WARME R. DOSSIER :
Elève
TRAVAUX AUTO - FORMATIFS
|
||
|
NOM : ……………………………… |
Prénom : ………………………….. |
Classe :………………….. |
|
Année scolaire : ……………………… |
Dossier
pris le : ……/………/……… |
Validation
de la formation : O -
N Le : …………………………………….. Nom
du formateur : …………………… |
|
ETABLISSEMENT :
………………………………………….. |
||
|
Corrigé des travaux
auto - formation. |
|
|
TRAVAUX
d ’ AUTO - FORMATION |
|
|
N°20 |
sur PYTHAGORE Le théorème ; la Propriété de PYTHAGORE et sa réciproque. |
|
Pré requis : a) Que signifie l’expression
« résoudre un triangle » ? b) Citer les deux méthodes qui permettent de
résoudre un triangle ? c) Citer les
possibilités permettant d ’ identifier les caractéristiques d’ un
triangle rectangle (mesures d’angle et de longueurs) par le calcul. |
|
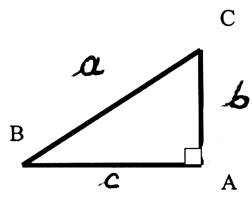
1°) énoncer le théorème de Pythagore.
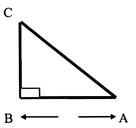
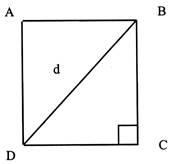
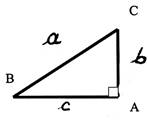
2°) Soit le demi carré :
|
a)Etablir la relation permettant
de calculer : BC ² = b) Donner la relation permettant
de calculer A B = |
|
3°) Enoncer
la réciproque de Pythagore.
4°)Que signifie l’expression « résoudre
un triangle »
5°)
Citer les deux méthodes qui permettent de résoudre un triangle ?
6°) Citer
les possibilités permettant d ’
identifier les caractéristiques d’ un triangle rectangle (mesures d’angle et de
longueurs) par le calcul.
7°)
Citer 3 possibilités permettant d ’ identifier un triangle rectangle .
Consignes : cette
évaluation comporte 4 parties :
Deux séries d’exercices (faire une série minimum ) ; des
exercices problèmes , des situations problèmes (interdisciplinaires).
|
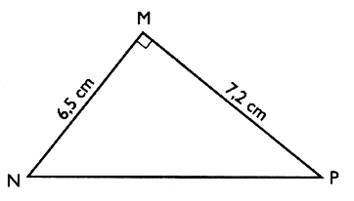
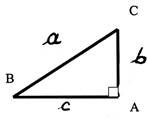
1°) Soit un triangle rectangle
NMP , rectangle en M . Ecrire la relation de
Pythagore.(avec des lettres) Calculer NP . |
|
2°) Réciproque :
a) Le triangle BAC dont les
côtés mesurent respectivement : 30 ; 40 ; 50 mm ; est - il rectangle .
b) Le triangle BAC dont les
côtés mesurent respectivement : 15 ; 20
; 30 mm ; est - il ? .
4°) Calculs sur la recherche de la troisième dimension du
triangle rectangle.
Faire les exercices
suivants : ( voir le cours pour le
corrigé)
|
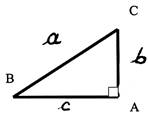
a) On donne : AC = 4 ; AB = 3 ; Calculer CB |
|
|
b) On donne : BC = 20 ; AC = 16 ; Calculer AB. |
|
|
c) On donne : BC = 42
; AB = 21 ; Calculer de
AC. |
|
Série II
4°) Niveau référentiel
(niveau V)
Compléter le tableau
|
|
|
Triangle 1 |
Triangle 2 |
Triangle 3 |
Triangle 4 |
Triangle 5 |
|
a |
|
37 cm |
|
0,65 m |
295 mm |
|
|
b |
450 mm |
35 cm |
45 cm |
|
2,36 dm |
|
|
c |
600 mm |
|
280 mm |
0,33 m |
|
|
|
|
|
|
|
|
|
Série II
|
N°1 |
|
Données : |
Résolution : |
|
BA = 108 mm |
|
||
|
CA = 45 mm |
|
||
|
Calculer : |
|
||
|
« a » = ? |
|
|
N°2 |
|
Données : |
Résolution : |
|
|
|
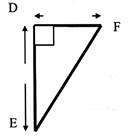
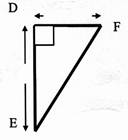
DF = 127 mm |
|
|
DE = 156 mm |
|
||
|
Calculer : FE = x
; à 0,1 mm prés |
|
||
|
|
|
|
N°3 |
|
Données : |
Réponse : |
|
|
|
CA = 74 cm |
|
|
CB = 24 cm |
|
||
|
Calculer AB. |
|
||
|
|
|
||
|
|
|
Données : |
Réponse : |
|
|
|
NM = 13,75 cm |
|
|
NT = 11 cm |
|
||
|
Calculer TM |
|
||
|
|
|
|
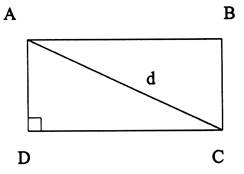
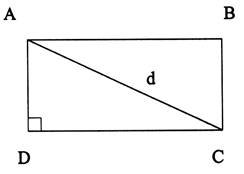
N°5 |
Application :
Diagonale d’un rectangle |
Données : |
Résolution : |
|
|
|
AB = 170 cm |
|
|
BC = 95 cm |
|||
|
Calculer AC =
« d » ( à 0,1 cm prés.) |
|||
|
|
|
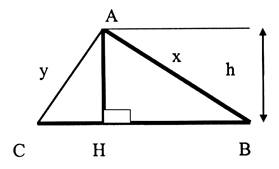
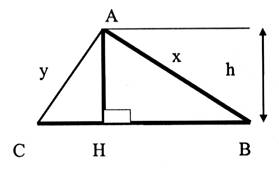
N°6 |
Triangle quelconque : |
Données : |
Résolution : |
|
|
|
CB = 114 cm |
|
|
HB = 71 cm |
|||
|
« h » = 83
cm |
|||
|
Calculer : AB = x ( à 1 mm prés) AC = y (à 1 mm prés) |
|||
|
N°7 |
La diagonale d’un carré |
Données : |
Résolution |
|
|
|
BC = 32 dm |
|
|
En déduire la valeur de AB ; CD ; AD. Calculer BD ( = d)
à 1 cm prés. |
|||
|
7 b ++ |
Etudier le cas où AB = 1 dm
: d = racine de 2 |
|
|
|
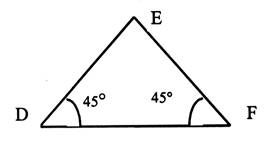
N°8 |
Le triangle rectangle
isocèle |
Données : |
Réponse : |
|
|
|
-Calculer l’angle E : -Quelle est la nature du
triangle ? -DE = 160 cm En déduire EF Calculer DF |
|
|
|
|||
|
8 b ++ |
Calculer « DE » si « DF » est égal à 6 cm
|
|
|
|
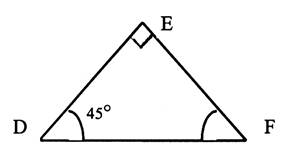
8c |
|
Données : |
Réponse : |
|
|
|
Calculer l’angle F : -Quelle est la nature du
triangle ? -DE = 160 cm En déduire EF Calculer DF |
|
|
|
|
|
|
|
N°9 |
|
Données : |
Réponse : |
|
|
|
Sachant que DC = 31 m |
|
|
CB = 33 m et
BA= 56 m |
|
||
|
Calculer AC (
à 0,1 m prés) |
|
||
|
|
|
||
|
N° 10 a |
|
Données : |
Réponse : |
|
|
|
En déduire l’angle C |
|
|
Que peut -on dire du
triangle ACB , au regard du triangle ADB ? |
|
||
|
Quelles sont les valeurs
des angles : A CB = D C A = C D A = CAD = La longueur de : AB = 100 mm En déduire CB Calculer : AC (au mm prés) |
|
||
|
|
|
||
|
10 b +++ |
On donne AC = 60 ,
calculer la valeur de AB puis BC |
|
|
|
N°10 c |
|
Données : |
Réponse : |
|
|
|
En déduire l’angle C |
|
|
Que peut -on dire du
triangle ACB , au regard du triangle ADB ? |
|
||
|
Quelles sont les valeurs
des angles : A CB = D C A = C D A = CAD = La longueur de : AB = 100 mm En déduire CB Calculer : AC (au mm prés) |
|
||
|
|
|
||
|
10 b +++ |
On donne AC = 60 ,
calculer la valeur de AB puis BC |
|
|
|
N°10 |
|
Données : |
Réponse : |
|
|
|
En déduire l’angle C Que peut -on dire du triangle
ACB , au regard du triangle ADB ? Quelles sont les valeurs
des angles : A CB = D C A = C D A = CAD = La longueur de : AB = 100 mm En déduire CB Calculer : AC (au mm prés) |
|
|
10 b +++ |
On donne AC = 60 , calculer
la valeur de AB puis BC |
|
|
PB NIVEAU IV :
APPLIQUATION :
PRISME DROIT
|
N° |
Figure |
Données : |
Réponse : |
|
|
|
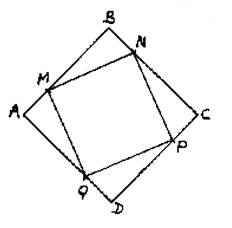
Soit le carré ABCD. On sait que : AB= 60 mm AM = BN = CP = DQ = 15 mm On demande : 1°) Calculer les dimensions
du carré MNPQ. 2°) Niveau + comparer les deux aires. |
|
|
N° |
Figure |
Données : |
Réponse : |
|
|
|
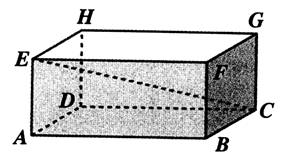
ADCB est la base du prisme.. Les dimensions du
parallélépipède rectangle sont : (en mm) L = 120 mm ; Largeur = 40 mm Hauteur = 30 mm Calculer la
longueur : EB = BG = EC = |
|
|
N° |
Figure |
Données : |
Réponse : |
|
|
|
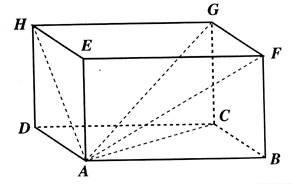
DCBA est la base du prisme.. Les dimensions du
parallélépipède rectangle sont : (en mm) L = 100 mm ; Largeur = 40 mm Hauteur = 40 mm Calculer la
longueur : HA = GA = FA = CA = |
|
|
N° 14 |
Problème : niveau
V Parallélépipède rectangle
. |
Données : |
|
|
|
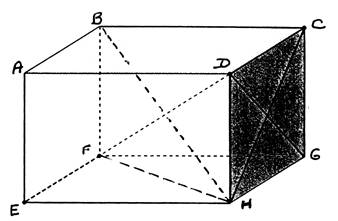
Les dimensions du prisme
droit sont : 6 cm X
4 cm X 3 cm la vue de face mesure 6 cm par 3 cm. 1°) Tracer le prisme en perspective cavalière. 2°) Calculs : Calculer ED Calculer FH Calculer HC 3°) calculer la surface
latérale du prisme. 4°) calculer la surface
totale du prisme. 5°) Calculer le volume du
prisme. 6°) Calculer la masse du
prisme ( masse volumique = 1,2 kg / dm3 7°) Calculer le poids du
prisme. |
||
PB NIVEAU IV :
|
N° 4 |
Figure |
Données : |
|
|
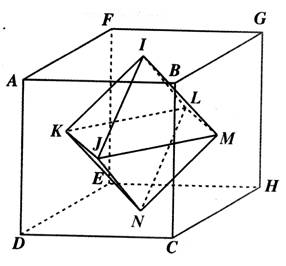
Soit un cube dont l’arête
mesure 60 mm. Les points I, J, K, L, M, N, sont les centres des faces du cube . a)
Combien
de faces a le solide « I J K L M N » ? Montrer simplement que toutes ses arêtes
sont égales. b)
Calculer
la longueur d’une arête , EM par
exemple. c)
Calculer
le volume de la pyramide « KLMJI » , en déduire le volume du
solide : « I J K L M N » |
|
SUITE Devoir de préparation N°2:
Niveau référentiel
(niveau V) ( si ? SOS Cours)
Compléter le tableau
|
|
|
Triangle 1 |
Triangle 2 |
Triangle 3 |
Triangle 4 |
Triangle 5 |
|
a |
|
370 mm |
|
65 cm |
2,95
dm |
|
|
b |
45 cm |
350 mm |
450 mm |
|
23, 6 cm |
|
|
c |
60 cm |
|
28 cm |
0,33 m |
|
|
|
|
|
|
|
|
|
Série II
|
N°1 |
|
Données : |
Résolution : |
|
BA = 10,8 cm |
|
||
|
CA = 45 mm |
|
||
|
Calculer : |
|
||
|
« a » = ? |
|
|
N°2 |
|
Données : |
Résolution : |
|
|
|
DF = 127 mm |
|
|
DE = 1,56 dm |
|
||
|
Calculer : FE = x
; à 0,1 mm prés |
|
||
|
|
|
|
N°3 |
|
Données : |
Réponse : |
|
|
|
CA = 740 mm |
|
|
CB = 24 cm |
|
||
|
Calculer AB. |
|
||
|
|
|
||
|
|
|
Données : |
Réponse : |
|
|
|
NM = 13,75 dm |
|
|
NT = 11 cm |
|
||
|
Calculer TM |
|
||
|
|
|
|
N°5 |
Application :
Diagonale d’un rectangle |
Données : |
Résolution : |
|
|
|
AB = 170 mm |
|
|
BC = 9,5 cm |
|||
|
Calculer AC =
« d » ( à 0,1 cm prés.) |
|||
|
|
|
N°6 |
Triangle quelconque : |
Données : |
Résolution : |
|
|
|
CB = 11,4 d |
|
|
HB = 71 cm |
|||
|
« h » = 83
0 mm |
|||
|
Calculer : AB = x ( à 1 mm prés) AC = y (à 1 mm prés) |
|||
|
N°7 |
La diagonale d’un carré |
Données : |
Résolution |
|
|
|
BC = 3,2 m |
|
|
En déduire la valeur de AB ; CD ; AD. Calculer BD ( = d)
à 1 cm prés. |
|||
|
7 b ++ |
Etudier le cas où AB = 1 dm
: d = racine de 2 |
|
|
|
N°8 |
Le triangle rectangle
isocèle |
Données : |
Réponse : |
|
|
|
-Calculer l’angle E : -Quelle est la nature du
triangle ? -DE = 1,60 m En déduire EF Calculer DF |
|
|
|
|||
|
|
|||
|
|
|||
|
8 b ++ |
Calculer DE si
DF est égal à 6 cm
|
|
|
|
N°9 |
|
Données : |
Réponse : |
|
|
|
Sachant que DC = 3,1 m |
|
|
CB = 3,3 m et
BA= 5,6 m |
|
||
|
Calculer AC (
à 0,1 m prés) |
|
||
|
|
|
||
|
N°10 |
|
Données : |
Réponse : |
|
|
|
En déduire l’angle C |
|
|
Que peut -on dire du
triangle ACB , au regard du triangle ADB ? |
|
||
|
Quelles sont les valeurs
des angles : A CB = ; D C A
= ; C D A = CAD = 60 cm |
|||
|
|
|
||
|
10 b +++ |
On donne AC = 60 ,
calculer la valeur de AB puis BC |
|
|
|
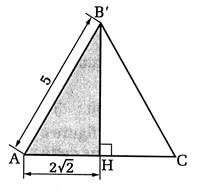
11°) Calculer B’ H : Le triangle est -il isocèle ou équilatéral ? |
|
Fin du devoir n°2
APPLIQUATIONS Autres séries
d'exercices
|
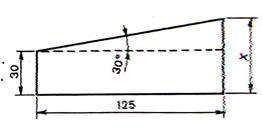
1°) Calculer la longueur « x » |
|
|
|
|
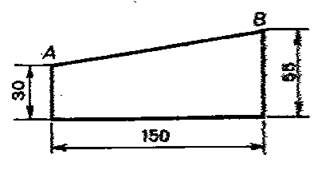
2°) Calculer la longueur « x » |
|
|
|
|
3°) Calculer la diagonale d’un cube de 1 m d’ arête . |
|
|
|
|
4°) Calculer la diagonale d’un parallélépipède rectangle ayant pour dimensions 7 ;
8 et 10 cm . |
|
|
|
|
5°) Calculer la diagonale d’un carré de 2,5 dm de côté |
|
|
|
|
6°)Calculer la longueur de AB |
|
||
|
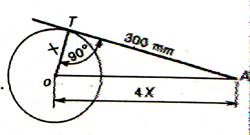
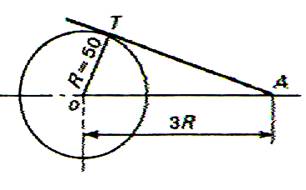
7°) Calculer la longueur de la tangente AT (côtes en mm ) |
|
|
|
INTERDISCIPLINARITE :
Dans le bâtiment : pour effectuer
un pavage dans une pièce .
|
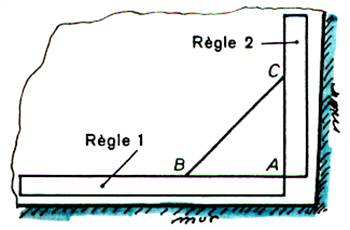
Ce procédé permettant de
tracer une droite perpendiculaire par
exemple pour le pavage
d’une pièce @ . ( les murs n’étant
pas eux mêmes perpendiculaires ) On mesure AB = 6O cm sur
la règle 1 , qui sert de base , puis on mesure AC = 80 cm sur la règle 2 , et
on déplace la règle 2 de façon que BC mesure 1m. Les deux bords AB et AC
forment un angle droit. |
|
Remarques : Sur une
surface plus réduite , on pourrait porter
AB = 6 cm AC = 8 cm ; il faut que
BC mesure 10 cm .
Ou AB = 3 cm AC = 4
cm ; il faut que BC mesure 5 cm .
Ou AB = 12 cm AC = 16
cm ; il faut que BC mesure 20 cm .
Voir aussi la « corde à 13 nœuds ».
PROBLEMES DIVERS :
|
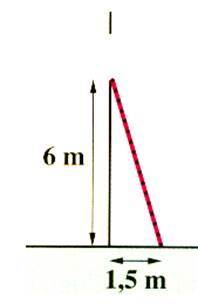
N°1 : Quelle longueur
doit mesurer une échelle pour atteindre une fenêtre située à 6 m. Si on lui
donne 1,5 mètres de pied ? |
|
|
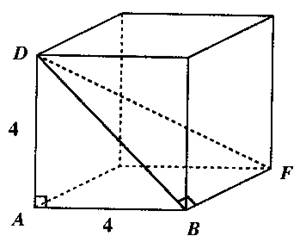
N° 2 : Calculer la
diagonale du cube au dixième près. Réponse : DB » 5,7 DF » 6,9 |
|
|
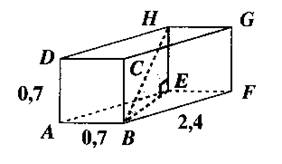
N°3 Calculer la longueur de la diagonale du segment BH , au dixième près. |
|
|
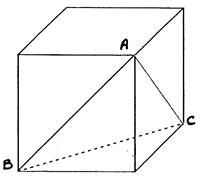
N°4 : Le cube à 5 cm
d’arête. Calculer BA , AC et BC. Quelle est
la nature du triangle BAC. ? |
|