Pythagore Niveau V

Pré requis : « @ PYTHAGORE TRACES »

Leçon

CALCULS

N°20

sur PYTHAGORE

théorème ; la Propriété de PYTHAGORE et sa réciproque.

Pré requis :

a) Que signifie l’expression « résoudre un triangle » ?

b) Citer les deux méthodes qui permettent de résoudre un triangle ?

c) Citer les possibilités permettant d ’ identifier les caractéristiques d’ un triangle rectangle (mesures d’angle et de longueurs) par le calcul.

Préparation devoir (2)

SUITE Devoir de préparation N°2:

Niveau référentiel (niveau V) ( si ? SOS Cours)

Compléter le tableau

	Triangle 1	Triangle 2	Triangle 3	Triangle 4	Triangle 5
a		370 mm		65 cm	2,95 dm
b	45 cm	350 mm	450 mm		23, 6 cm
c	60 cm		28 cm	0,33 m

Série II

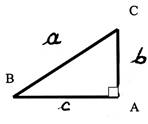
N°1	Données :	Résolution :
	BA = 10,8 cm
	CA = 45 mm
	Calculer :
	« a » = ?

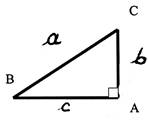
N°2	Données :	Résolution :
	DF = 127 mm
	DE = 1,56 dm
	Calculer : FE = x ; à 0,1 mm prés

N°3	Données :	Réponse :
	CA = 740 mm
	CB = 24 cm
	Calculer AB.

	Données :	Réponse :
	NM = 13,75 dm
	NT = 11 cm
	Calculer TM

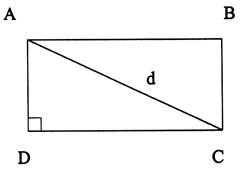
N°5	Application : Diagonale d’un rectangle	Données :	Résolution :
		AB = 170 mm
		BC = 9,5 cm
		Calculer AC = « d » ( à 0,1 cm prés.)

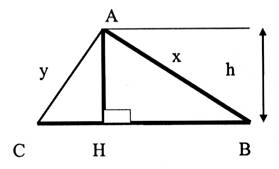
N°6	Triangle quelconque :	Données :	Résolution :
		CB = 11,4 d
		HB = 71 cm
		« h » = 83 0 mm
		Calculer : AB = x ( à 1 mm prés) AC = y (à 1 mm prés)

N°7	La diagonale d’un carré	Données :	Résolution
		BC = 3,2 m
		En déduire la valeur de AB ; CD ; AD. Calculer BD ( = d) à 1 cm prés.
7 b ++	Etudier le cas où AB = 1 dm : d = racine de 2
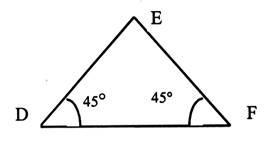
N°8	Le triangle rectangle isocèle	Données :	Réponse :
		-Calculer l’angle E : -Quelle est la nature du triangle ? -DE = 1,60 m En déduire EF Calculer DF



8 b ++	Calculer DE si DF est égal à 6 cm

N°9	Données :	Réponse :
	Sachant que DC = 3,1 m
	CB = 3,3 m et BA= 5,6 m
	Calculer AC ( à 0,1 m prés)

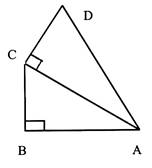
N°10	Données :	Réponse :
	En déduire l’angle C
	Que peut -on dire du triangle ACB , au regard du triangle ADB ?
	Quelles sont les valeurs des angles : A CB = ; D C A = ; C D A = CAD = 60 cm

10 b

+++

On donne AC = 60 , calculer la valeur de AB puis BC

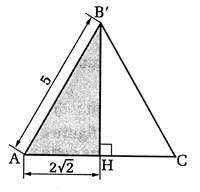
11°) Calculer B’ H :

Le triangle est -il isocèle ou équilatéral ?

Fin du devoir n°2

APPLIQUATIONS Autres séries d'exercices

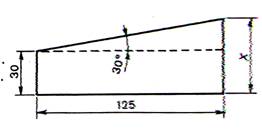
1°) Calculer la longueur « x »
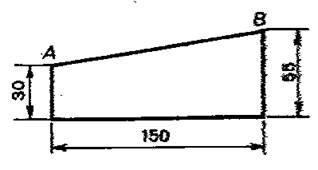
2°) Calculer la longueur « x »
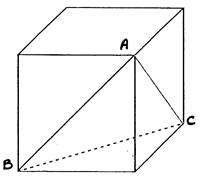
3°) Calculer la diagonale d’un cube de 1 m d’ arête .
4°) Calculer la diagonale d’un parallélépipède rectangle ayant pour dimensions 7 ; 8 et 10 cm .
5°) Calculer la diagonale d’un carré de 2,5 dm de côté
6°)Calculer la longueur de AB
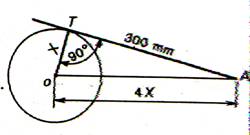
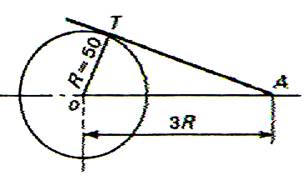
7°) Calculer la longueur de la tangente AT (côtes en mm )

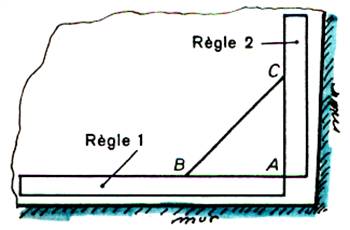
INTERDISCIPLINARITE :

Dans le bâtiment : pour effectuer un pavage dans une pièce .

Ce procédé permettant de tracer une droite perpendiculaire par exemple pour le pavage d’une pièce @ .

( les murs n’étant pas eux mêmes perpendiculaires )

On mesure AB = 6O cm sur la règle 1 , qui sert de base , puis on mesure AC = 80 cm sur la règle 2 , et on déplace la règle 2 de façon que BC mesure 1m.

Les deux bords AB et AC forment un angle droit.

Remarques : Sur une surface plus réduite , on pourrait porter ; AB = 6 cm AC = 8 cm ; il faut que BC mesure 10 cm .Ou AB = 3 cm AC = 4 cm ; il faut que BC mesure 5 cm .Ou AB = 12 cm AC = 16 cm ; il faut que BC mesure 20 cm .

Voir aussi la « corde à 13 nœuds ».

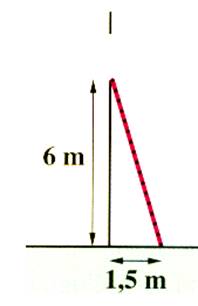
PROBLEMES DIVERS :N°1 : Quelle longueur doit mesurer une échelle pour atteindre une fenêtre située à 6 m. Si on lui donne 1,5 mètres de pied ?

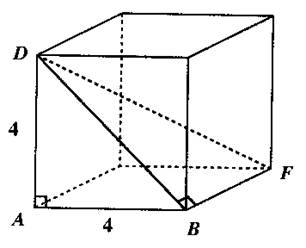
N° 2 : Calculer la diagonale du cube au dixième près.

Réponse :

DB » 5,7

DF » 6,9

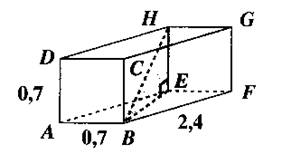
N°3 Calculer la longueur de la diagonale du segment BH , au dixième près.

N°4 : Le cube à 5 cm d’arête.

Calculer BA , AC et BC.

Quelle est la nature du triangle BAC. ?