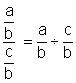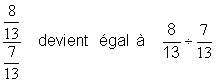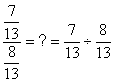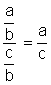|
Auteur :
WARME R.
LIVRE . Document non interactif ; pour obtenir le cours
interactif il faut posséder le code
|
||
|
NOM : ……………………………… |
Prénom : ………………………….. |
Classe :………………….. |
|
Année scolaire : ……………………… |
Dossier
pris le : ……/………/……… |
Validation
de la formation : O -
N Le : …………………………………….. Nom
du formateur : …………………… |
|
ETABLISSEMENT :
………………………………………….. |
||
|
|
|
||||
|
|
DOC : livre Elève .Cours interactifs - et travaux + corrigés. |
||||
|
Leçon TITRE : LES FRACTIONS DE MEME DENOMINATEUR (Opérations) |
|||||
|
« ADDITION » ;
« SOUSTRACTION » ; « MULTIPLICATION » ;
« DIVISION » de DEUX
FRACTIONS DE MEME DENOMINATEUR .CHAPITRES |
Niveau obtenu |
Bilan |
|||
|
1.Addition
, soustraction , multiplication et division de deux fractions de même dénominateur. |
|
|
|||
|
2..Addition
, soustraction , multiplication et division
de deux fractions de même dénominateur. |
|
|
|||
|
3.Addition , soustraction , multiplication et
division d ‘une fractions et d’un
nombre . |
|
|
|||
|
|
|
||||
|
|
|
|
|||
|
Définitions
préalables |
|||||
|
« Fraction » : La fraction est le rapport (une division ) d’un nombre entier naturel par
un autre nombre entier naturel |
|||||
|
Exemple :
|
|
|
|||
|
|
|
|
|||
|
« Rationnel » Un rationnel
est le quotient d’un entier par un entier « non nul ». ( on dit aussi : « différent de
zéro » ; noté : ¹ 0 ) |
|||||
|
Exemples : 16 : 2 = 9 9 est un rationnel 25:
4 = 6,25 6,25 est un rationnel 11
: 7 =
11/7 11/ 7 est un
rationnel |
|||||
|
« Ecriture fractionnaire »: On appelle « écriture fractionnaire « une
fraction possédant, au moins un nombre décimal ».( Il y a au moins un
nombre décimal au numérateur ou au dénominateur.) |
|||||
|
Pour des raisons « pratiques » il est souvent demandé d'exprimer le
résultat du calcul sous une forme qui vous est précisée:
exemple :« arrondi à …0,001… »
( pour plus d’information consulter
le CD : les « nombres irrationnels » . |
|||||
|
Savoir additionner deux fractions de même dénominateur (cas où les dénominateurs sont différents) |
|
||||
|
Savoir soustraire deux fractions de même dénominateur ; (cas où les
dénominateurs sont différents) |
|
||||
|
Savoir multiplier
deux fractions de même
dénominateur ; (cas où les dénominateurs sont différents) |
|
||||
|
Multiplication : pourcentage |
|
||||
|
Savoir diviser
deux fractions de même
dénominateur ; (cas où les dénominateurs sont différents) |
|
||||
|
Savoir diviser
un nombre par une fraction |
|
||||
|
Savoir diviser
une fraction par un nombre. |
|
||||
|
COURS |
||||||
|
Important :Pour faciliter les calculs et pour éviter les
risques d’erreurs de calcul , il est conseillé de simplifier jusqu’à rendre
irréductible la ou les fractions * chaque
opération est traitée, à chacune correspond une information plus particulière
. |
||||||
|
i9 |
|||||
|
1.
ADDITION de deux
fractions de MEME DENOMINATEUR |
Cd³ INFO 1 + |
||||
|
|
|
|||||
|
Définition : La
somme de deux fractions est égale à une troisième fraction qui aura pour « Numérateur » : la somme
des numérateurs et pour « Dénominateur » : le dénominateur
commun. |
||||||
Forme mathématique:
|
« a » et « c » sont les
numérateurs. |
|
On calcule la somme des numérateurs. « a + c » |
|||||
|
« b » est le dénominateur |
|
|
|||||
|
Exemple |
|
Le dénominateur commun aux
deux fractions est « b » |
|||||
|
Remarques : ( 15 /13 ) cette fraction ne peut plus « se
réduire », elle ne peut plus être simplifiée , on dit que la fraction
est « irréductible ». Si l’on fait la division de 15/13 on trouve » 1,15384615384615384615384615384615……... Ce nombre est donné par la calculatrice, la série
de chiffres «1538461 » se répète
à « l’infini » . |
|||||||
|
Calculer :
(avec des nombres entiers naturels) |
|
Calculer :
(avec des nombres entiers relatifs) |
|||||
|
|
|
|
|||||
|
|
|
|
|||||
|
i9 |
2. SOUSTRACTION de deux fractions de MEME
DENOMINATEUR |
Cd³ INFO 2+ |
||||
|
Règle :
(Forme littérale) |
|
||||||
|
Définition : La différence de deux fractions est égale à une troisième fraction
qui aura pour
« Numérateur » : la différence des numérateurs et pour
« Dénominateur » : le dénominateur commun. |
|||||||
|
|
|
||||||
Forme mathématique:
|
« a » et « c » sont les
numérateurs. |
|
On calcule la différence des numérateurs. « a - c » |
||||||||||||||||||||
|
« b » est le dénominateur
« commun » aux deux fractions. |
|
|
||||||||||||||||||||
|
Exemple Calculer : |
|
On conserve le dénominateur
commun aux deux fractions est « b » |
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
Remarques : ( 1/13 ) cette fraction ne peut plus « se
réduire », elle ne peut plus être simplifiée , on dit que la fraction
est « irréductible ») Si l’on fait la division de 1/13 on trouve » 0,333333333333333333333333333333333……... Ce nombre est donné par la calculatrice, le nombre
« 3 » se répète à « l’infini » . Formes
d’expressions du résultat : le résultat peut être exprimé sous forme
d’une fraction irréductible , ou sous forme décimale « exacte » ou
arrondie ( l’arrondi est fixé par
celui qui pose l’opération) Exemple :
l’opération peut s’exprimer |
||||||||||||||||||||||
|
Forme irréductible |
Forme décimale (affichage) Forme
décimale arrondi 33ème rang
décimal après la virgule : |
Forme arrondie : |
||||||||||||||||||||
|
|
0,333333333333333333333333333333333 |
0,33 à 0,01 prés |
||||||||||||||||||||
|
Calculs avec des
entiers naturels : |
|
Calcul avec des entiers relatifs : |
||||||||||||||||||||
|
Cas A : le calcul possible :
parce 8 - 7 est une opération
possible avec des nombres entiers naturels. |
|
A) Calculons :
|
||||||||||||||||||||
|
Cas B : le calcul n’est pas possible (impossible) :
parce « 7 - 8 » est une
opération impossible avec des nombres entiers naturels. |
|
|
||||||||||||||||||||
|
Remarque :
|
||||||||||||||||||||||
|
|
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
Résultats : |
|
|||||||||||||||||||||
|
|
|
|||||||||||||||||||||
|
i9 |
3.MULTIPLICATION de deux
fractions de MEME DENOMINATEUR |
|||||||||||||||||||||
|
Règle : ( Forme littérale) |
|
|||||||||||||||||||||
|
La multiplication de deux
fractions de même dénominateur est
égale à une troisième fraction qui aura pour: « Numérateur » le
produit des numérateurs et pour « Dénominateur » le produit des
dénominateurs. |
||||||||||||||||||||||
|
Forme symbolique mathématique: |
||||||||||||||||||||||
|
« a » et « c » sont les
numérateurs |
|
Le produit des numérateurs est : « ac » |
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
« b » est le dénominateur
« commun » aux deux fractions. |
|
Le produit des dénominateur est « b b » « b² » Le produit d’un nombre par lui - même est appelé « carré » |
||||||||||||||||||||
|
Remarque :
Des opérations avec 2 fractions ;la
multiplication de deux fractions est l’opération la plus simple. |
||||||||||||||||||||||
|
Exemples : |
||||||||||||||||||||||
|
Avec des nombres entiers naturels |
|
Avec des nombres entiers relatifs : |
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
Calculs : 8 fois 7 = 56 et 13² = 169 Expressions
du résultat : 1°) fraction irréductible : ( 56 / 169 ) 2°) lecture sur écran : » 0,331360946745562130177514792899 408 3°)Arrondi » 0,331 à 0,001 près . |
|
|
||||||||||||||||||||
|
|
les fractions n’ont pas le même
dénominateur ; ( (+13) est différent de (-13) ; voir la deuxième partie de cours sur le
produit de deux fractions de dénominateur différent. |
|||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
i9 |
4
.DIVISION de deux fractions de MEME DENOMINATEUR ( fraction de 2 fractions) |
Cd³ INFO + |
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
Remarque importante: Nous
ne pouvons pas calculer directement la fraction de deux fractions ,il faut
impérativement transformer : La fraction de fractions doit être transformée
en division de deux fractions |
||||||||||||||||||||||
|
On transforme la fraction de fractions
par une division d’une fraction par l’autre fraction. (en conservant
l’ordre) :à savoir que : La fraction en numérateur devient
« dividende » ; la fraction « dénominateur » devient
« diviseur ». |
|
|||||||||||||||||||||
|
Remarque importante : remarquer que la première fraction est au dessus de la barre de fraction principale , le signe « égal » est aligné avec ce trait . la deuxième fraction étant située sous la barre de
fraction alignée avec le signe égal. |
Application :
|
|
||||||||||||||||||||
|
Bien que la fraction de deux fractions soit
transformée en division ;le calcul de la
division de deux fractions ne se fait pas ; il faut « passer » par la multiplication
en respectant la procédure suivante: |
||||||||||||||||||||||
|
Procédure |
Modèle théorique |
Exemple : |
||||||||||||||||||||
|
1°) Première transformation :la
fraction de fractions en une division de deux fractions |
|
|
||||||||||||||||||||
|
2°) Deuxième transformation : la division en multiplication. Rappel ( Cd
³ ) INVERSE
d'un nombre.(ou
fraction) : On se souvient que : « Diviser un nombre « A » par un
nombre « B »revient à multiplier le premier nombre par l’inverse du
second nombre. » A : B = A ´ inv. B « A » est la première fraction et
« B » est la seconde fraction. Il suffit de remplacer : « : B » par «´ inv.
B » |
On se souvient que l’ inverse de |
on sait que :
|
||||||||||||||||||||
|
3ème transformation :. |
|
|
||||||||||||||||||||
|
4ème : on effectue la multiplication On a appliqué , les règles de la multiplication de deux fractions : remarque : « b : b = 1 » et « 13 : 13 = 1 » ce qui permet de simplifier les facteurs « B » et « 13 » |
|
on simplifie :
|
||||||||||||||||||||
|
5°) Conclusion : |
|
Conclusion :
Dans
le calcul de 7¸ 8 la valeur décimale est exacte
|
||||||||||||||||||||
|
Règle :
( forme littérale ) Pour
calculer la division de deux fractions il suffit de
multiplier la première fraction par l’inverse de seconde
fraction. |
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
Résultat : Le résultat de la division de deux fractions de même
dénominateur a pour numérateur le
numérateur de la première fraction et pour dénominateur le numérateur de la
seconde fraction . (voir ci dessus) |
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
+Faire les exercices suivants : |
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
Addition |
|
|
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
Soustraction ( pour
cet exercice il faut avoir fait la leçon sur les nombres relatifs) |
|
|||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
Soustraction |
|
|
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
Multiplication |
|
|
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
Fraction de fractions |
|
|
||||||||||||||||||||
|
|
= |
|
||||||||||||||||||||
|
Division de fractions |
|
|
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
Réponses :
|
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
Leçon |
Titre |
|||||||||||||||||||||
|
TRAVAUX
d ’ AUTO - FORMATION sur A.
ADDITION ; SOUSTRACTION ; MULTIPLICATION ; DIVISION
de DEUX FRACTIONS DE
MEME DENOMINATEUR .LES |
||||||||||||||||||||||
|
|
|
|||||||||||||||||||||
|
|
Définitions préalables |
|||||||||||||||||||||
|
1°) donner la
définition d’un fraction : donner un exemple avec les nombres « 3 » et « 4 » . Exemples ?: 2°) Qu’est ce qu’un
rationnel ? . Donner des exemples : 16 : 2 = ? ……………………………………………… 25: 4 =
? ……………………………………………… 11 : 7 =
? ………………………………………………… 3°) qu’appelle -
t - on
« écriture fractionnaire »
|
||||||||||||||||||||||
|
|
Cd³ INFO + |
|||||||||||||||||||||
|
1. ADDITION de deux
fractions de MEME DENOMINATEUR |
Cd³ INFO 1 + |
|||||||||||||||||||||
|
|
1°) A quoi est égale la somme de deux fractions ? ( Forme littérale) |
|
||||||||||||||||||||
|
|
2°) Donner |
|
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
2.SOUSTRACTION de deux fractions de MEME DENOMINATEUR |
Cd³ INFO 2+ |
|||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
1°) A quoi est égale la différence de deux fractions de
même dénominateur ? ( Forme
littérale) 2°) donner |
|
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
3.MULTIPLICATION de deux fractions
de MEME DENOMINATEUR |
Cd³ INFO + |
|||
|
. |
1°) A quoi est égale la différence de deux fractions de
même dénominateur ? ( Forme
littérale) |
|
||
|
|
2°) donner sa forme symbolique mathématique:
|
|
||
|
|
|
|
||
|
4 .DIVISION de deux fractions de MEME DENOMINATEUR |
Cd³ INFO + |
|||
|
|
|
|
||
|
|
1°) Compléter la phrase : Remarque importante: Nous …………………….
calculer directement la fraction de deux fractions ,il faut impérativement
transformer 2°) Transformer la fraction de fractions en division de
fractions :
3°) A quoi
est égale le résultat de la division
de deux fractions de même dénominateur ? ( Forme littérale) 5° )
montrer les étapes de transformation conduisant au résultat .
|
|
||
|
|
Définitions préalables 1°) avec 3 et 4
écrire une fraction ? 2°) souligner
les rationnels . 16 + 2 = 18
; 16 : 2 = 8 ; 16 -2 = 14 25: 4 =
6,25 ; 25 ´ 4 = 100 ; 25 - 4
= 21 11 + 7 =
18 ; 7 - 11 = -4 ; 11 : 7 =
11/7 3°) entourer l ’
« écriture fractionnaire » 16 /
2 ; 17 / 5 ;
20,2 / 2 ; 10 / 0,5 ;
6,3 / 7,8 ; .456/ 3625 |
|
||
|
EVALUATION : |
Cd³ INFO + |
|||
|
1. ADDITION de DEUX
FRACTIONS DE MEME DENOMINATEUR . |
Cd³ INFO 1 + |
|||
|
|
|
|
|
|
Calculer :
|
|
|
|
|
|
|
2. SOUSTRACTION de DEUX
FRACTIONS DE MEME DENOMINATEUR . |
Cd³ INFO 2+ |
|
|
|
|
|
Calculer : |
|
|
|
3. MULTIPLICATION
de DEUX
FRACTIONS DE MEME DENOMINATEUR . |
Cd³ INFO 1 + |
|
|
|
|
|
|
Calculer :
|
|
|
|
|
|
|
4. DIVISION de DEUX FRACTIONS DE
MEME DENOMINATEUR . |
Cd³ INFO 2+ |
|
|
|
|
|
Calculer : |
|
|