Pré requis:

Les grands nombres.
Lecture : les unités	�
Lecture : La numération dans N	�
Lecture : Notions de grandeur , de « numération et de nombre	�
Nomenclature sur les chiffres et les nombres	�
Informations *sur N**	�
Lire : relations d’ordre avec les entiers naturels .	24

ENVIRONNEMENT du dossier :

				CLASSE 6^ème ( avant 2000)
Index	Objectif précédent: 1°)Classe des unités simples 2°) classe des mille. 3°) classe des millions et plus. 4°) Cours précédent ( 6^ème ) sur :l es entiers	Dossier N°	Info +++ : Les entiers naturels. Objectif suivant :1°) addition dans N 2°) classification des nombres entiers 3°)Info sur la numération des nombres décimaux 4° ) Les nombres entiers   « numération  romaine » 5°) Numération des nombres décimaux	1°)Tableau 14 2°) liste des activités dans N 3°) les N en primaires.( travaux et rappels de cours) Vers le programme de 6éme (2012)

DOSSIER : LES ENTIERS NATURELS (symbole : N ) : Les 3 premières opérations

	1°) ADDITON des entiers naturels .
	( a) propriétés de l’addition de des nombres entiers naturels. ;b) utilisation des parenthèses , c) ordre de grandeur d’une somme ) ; d) groupement de termes.
	2°) SOUTRACTION des entiers naturels
	a) découverte ;b)égalités ayant le même signification ; c) ordre de grandeur d’une différence, d) calcul mental : ajouter ,retrancher ;
	3°) MULTIPLICATION des entiers naturels
	a) définition ; b) propriétés ; c) ordre de grandeur d’un produit ; d) groupement de facteurs ; e) décomposition de 10 ; 100 ; 1 000 en un produit de facteurs.
	4°) Problèmes avec des entiers naturels
TEST		COURS	Devoir Contrôle	Devoir évaluation		Corrigé Contrôle	Corrigé évaluation
1°) Interdisciplinarité		2°) situations problèmes	3°) autres séries	4°) Fiche d’exercices.	5°) autres séries

Aller vers : Numération romaine

15

COURS

ADDITION des entiers naturels

Info

On a déjà étudié l’addition des entiers à l’école primaire ,et vu les tables de l’addition.

Ainsi : 8 + 3 = 11

« 11 » est appelé « la somme » de « 8 » et de « 3 »

« 8 » et « 3 » sont appelés « les termes » de la somme.

a) Propriétés de l’addition des nombres entiers naturels.

· 3 + 0 = 3 ; 0 + 7 = 7 ; « n » étant un entier naturel quelconque , «  n + 0 = n » ; on dit que «  0 » est « élément neutre de l’addition des entiers naturels ».

· 4 + 5 = 9 ; 5 + 4 = 9 ; on constate que 4 + 5 = 5 + 4

Si l’on change la valeur des entiers naturels , on fera toujours la même constatation . On ne change pas la somme de deux entiers si l’on permutte ces deux nombres. On dit alors que l’addition des entiers naturels est « commutative » Cette propriété s’appelle la « commutativité » de l’addition des entiers naturels.

b) Utilisation de parenthèses :

On doit savoir que « les parenthèses » indiquent que l’on doit effectuer en priorité les calculs figurant à l’intérieur.

Ainsi ,le calcul de «  15 + ( 11 + 7 ) » s’effectue de la façon suivante :

15 + ( 11 + 7 ) = 15 + 18 = 33

· De même le calcul : s’effectue 25 + ( 37 + 4 ) = 25 + 41 = 66

· Il se peut que qu’il y ait des parenthèses « imbriquées » Exemple : 7 + ( ( 6 + 2 ) + 5 ) = 7 + ( ( 8 ) + 5 ) = 7 + ( ( 13 ) ) = 20

Activité : Calculer ainsi : 9 + ( 2 + ( 3 + 7 ) ) =

c) Ordre de grandeur d’une somme : (et encadrement)

Toutes les fois que l’on fait une opération sur des nombres , il est bon de déterminer mentalement un ordre de grandeur du résultat afin d’éviter de commettre des erreurs grossières.

· En additionnant « 54 384 » et « 3462 » , on a trouvé « 88 456 » ; on va montrer , sans faire le calcul , que ce résultat est faux . « 54 384 » est voisin de « 54 000 » , et , « 3462 » est très voisin de « 3 000 » ; donc la somme est voisine de « 57 000 » et donc ne peut être égale à « 88 456 »

· Pour être plus précis , on peut dire que «  54 000 < 54 384 < 55 000 et 3 000 < 3462 < 4 000 Donc « 54 384  +  3462 » est supérieur à « 57 000 » et inférieur à «  59 000 » , si on donne un ordre de grandeur de cette somme on peut donner « 58 000 ». Activité de calcul : si l’on effectue le calcul « 54 384  +  3462 » on trouve : « 57 846 »

Exercice 1 : Un des nombres ci-dessous est égal à 7 432 + 56 308 ; trouvez ce nombre sans faire ( poser) l’addition . entourer la valeur ;;

135 740

62 740

12 840

63 740

Exercice 2 :

Sans faire (poser) l’addition, déterminez mentalement l’ordre de grandeur de :

31 672 + 58 347 + 17 035 + 83 977

Réponse :

( 31 + 58 + 17 + 84 =…..( 4+7+8+1) soit « 20 » on pose « 0 » et la retenue 2+ 8+1+5+3 soit 19 d’où 190 ..mille)

Effectuer la vérification en posant et faisant l’addition …

d) Groupement de termes .

Exemple : soit une addition de plus de deux nombres et contenant des parenthèses : et posée de deux façons différentes : ( 17 + 23 ) + 36 et 17 + ( 23 + 36 )

Première recherche du résultat .

Deuxième recherche du résultat:

( 17 + 23 ) + 36 = = (40 ) + 36 = 40 + 36 = 76

17 + ( 23 + 36 )= = 17 + ( 59 ) = 17 + 59 = 76

On constate que l’on trouve le même résultat dans les deux cas . : On peut donc écrire l’égalité  : ( 17 + 23 ) + 36 = 17 + ( 23 + 36 ) On peut conclure que la place des parenthèses n’est pas importante.

Activité :

a) Compléter les calculs :

( 24 + 13 ) + 33 =

24 + (13 + 33) =

( 24 + 33 ) + 13=

On peut « permuter » les termes de l’addition , cela ne change pas le résultat

b) Choisissez d’autres entiers ( à 1 ou 2 chiffres) , et compléter les calculs.

( ….. + …. ) + …… =

…….. + (…… + …..) =

Ecrivez l’égalité qui en résulte : ……………………………………………………………………

=

=

· Vous pouvez recommencer avec n’importe quels entiers , vous constaterez toujours que la valeur de la somme ne change pas si l’on place différemment les parenthèses. On dit alors que : l’addition des nombres entiers naturels est une opération « associative ». Cette propriété s’appelle : « l’associativité » de l’addition.

Activités série 1 :

· Vous allez calculer «  A = 13 + 56 + 19+ 23 » en plaçant des parenthèses de différentes façons :

1^ère façon : «  A = ( 13 + 56 + 19 ) + 23 » Effectuez le calcul : «  A = ( ……… + ……….) + ………. » = ……………+ ……………= ……………..

· Imaginez d’autres façons de placer les parenthèses puis effectuez le calcul :

2^ème façon : «  A = 13 + 56 + 19 + 23 » =………………………………………………………………………………………………..

3^ème façon : «  A = 13 + 56 + 19 + 23 » =……………………………………………………………………………………………

· Pour calculer une somme , il est possible d’utiliser à la fois la commutativité et l’associativité afin de regrouper des termes dont la somme est un nombre se terminant par zéro .« 0 ».

Exemple : 23 + 32 + 47 + 18 = ( 23 + 47 ) + ( 32 + 18 ) = 70 + 50 = 120

Faites de même pour l’expression « C »

C = 22 + 37 + 54 + 48 + 73 + 45 + 36 C = ( 22 + 48 ) + ( …..+……)+ ( …..+ ….) + …….. C = ……+ …….+ …….+ …….. C = ……….

Faites de même pour l’expression « D »

D = 85 + 72 + 53 + 14 + 26 + 11+ 48 + 25 + 69 + 7 D = …………………………………………………………………………………………………………… D = …………………………………………………………………………………………………………..

Activités série 2 :

Trouvez toutes les manières possibles d’écrire « 15 » sous forme d’une somme de trois nombres entiers distincts choisis parmi les nombres : 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9 ;

Exemple : 15 = 1 + 6 + 8 ; l’addition étant commutative , « 1 + 6 + 8 » est la même solution que « 8 + 1 + 6 »

SOUSTRACTION des entiers naturels

Cherchons le nombre qu’il faut ajouter à « 7 » pour obtenir « 10 » soit : 10 = 7 + …. ( 3) Le nombre « 3 » est appelé la différence de « 10 » et « 7 » pris dans l’ordre.. On écrit alors «  10 – 7 = ….. » ; « 10 » et « 7 » sont appelés les termes de la différence. L’opération correspondante s’appelle la « soustraction »

· Exemple de situation problème : Vous allez chez le libraire et vous acheté 2 livres pour un total de 42 € . Le premier livre coûte 17 € . Cherchons combien coûte le deuxième livre. 42 = 17 + ……. Pour trouver le résultat on fait la différence de « 42 » et « 17 » pris dans cet ordre. 42 - 17 = ……….

42 – 17 = …25.. signifie que : 42 = 17 + 25

· Cherchons si il est possible de calculer 13 – 15

Supposons qu’il existe un entier naturel ( ? ) égal à la soustraction «  13 – 15 »

Dans ces conditions , « 15 » ajouté à ce nombre ( ?) serait égal à « 13 » Ce qui est impossible car la somme de deux entiers naturels est toujours supérieure ou égale à chacun de ces nombres. Donc il n’existe pas d’entier naturel égal à «  13 – 15 ».

On voit alors que si ce calcul n’est pas possible, c’est parce que «  13 < 15 » ( 13 est inférieur à 15)

A retenir :

La différence de deux entiers naturels pris dans un ordre certain (dans un certain ordre) est l’entier naturel ( si il existe) qu’il faut ajouter au second pour obtenir le premier. Pour deux nombres entiers naturels , la soustraction n’est possible que si le premier nombre est supérieur ou égal au second.

« a - b = x » signifie que « a = b + x »

· Calcule si cela est possible : 7 – 4 = …………………… et 4 – 7 = ………………..

Peut- on 7 – 4 = ? = 4 – 7

On doit en déduire que la soustraction n’est pas commutative.

( 35 – 17 ) – 8 =………………………….. =…………………………….

35 - ( 17 – 8 ) =………………………………… =………………………………..

Trouvez vous le même résultat ? ……………………………………….. Donc ( 35 – 17 )- 8 – 8 - ( 17 – 8 ) La place des parenthèses importe –t-elle ?..................................................................................... On en déduit que la soustraction ……………………………………………………………………….

Exercice :

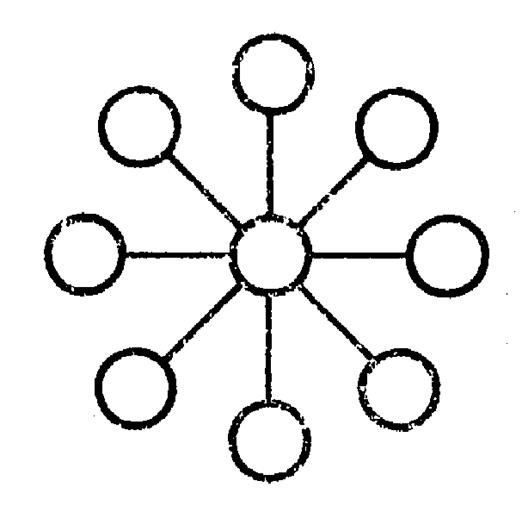
Disposez les nombres 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9 ; dans les ronds de l’étoile ci contre de telle sorte que la somme sur « chaque ligne » soit égale à « 15 »

b) Egalité ayant la même signification.

Dans chacune des lignes ci-dessous, les égalités ont la même signification. Complétez ces égalités en commençant par celle qui vous paraît la plus facile.

13 - 8 =…………

« signifie »

13 = …….+ ………

« signifie »

13 - …… = 8

25 - 4 =…………

« signifie »

……=…………………….

« signifie »

…………………………….

54 - … =…26…

« signifie »

………..= …….+ ………

« signifie »

………….-……….=……….

………….- 14 = 23

« signifie »

………..= …….+ ………

« signifie »

……….-……….=…14 .

25 – 0 = ………….

« signifie »

………..= …….+ ………

« signifie »

……………………………..

13 – 17 = …………….

« signifie »

13 = 17 + ……….

…………………………………………………………………..

27 – 27 = ………………

« signifie »

………..= …….+ ………

« signifie »

………………………………..

28 - …………..= 32

« signifie »

28 = ………+ 32

……………………………………………………………

c) Ordre de grandeur d’une différence.

Comme pour une somme, on peut déterminer un ordre de grandeur d’une différence.

Exemple : Cherchons un ordre de grandeur de « 58 399 – 21 356 »

Cherchons l’ordre de grandeur de chaque nombre : « l’ordre de grandeur de 58 399 est 59 000 , ( ou il est possible : 60 000 ) » ; « l’ordre de grandeur de 21 356 est 21 000 (ou il est possible : 20 000 ) »

Un ordre de grandeur de « 58 399 – 21 356 » est « 59 000 – 21 000  soit 38 000» ou il est possible « 60 000 – 20 000 soit 40 000 » le résultat est donc proche de 38 000 pour un cas ou 40 000 pour l’autre cas .

Info ++

d) Calcul mental :

1°) Ajouter « 9 » ; « 19 » ; « 29 » ;……etc.

· on sait que «  9 = 10 -1 » , ainsi : ajouter « 9 » revient à ajouter « 10 » puis retrancher « 1 »

Exemple : 46 + 9 = (46 + 10) - 1 = 55

Le chiffre des dizaines a augmenté de « 1 » et le chiffre des unités a diminué de »1 ».

Compléter :

57 + 9 =

95 + 9 =

143 + 9 =

· 19 = 20 -1 ; 65 + 19 = ( 65 + 20 ) – 1 = 85 -1 = 84

Compléter :

48 + 19 =

27 + 69 =

39 + 123 =

54 + 159 =

54 + 109 =

637 + 999 =

Remarque ; de la même façon 25 + 8 = ( 25 + 10 ) – 2 = 35 – 2 = 33

Et 34 + 27 = ( 34 + 30 ) – 3 = 64 – 3 = 61

Compléter :

44 + 38 = …………………..

56 + 98 = ……………….

25 + 107 = ………………

2°) Retrancher « 9 » ; « 19 » ; « 29 » ;……etc.

· 9 = 10 – 1 ; retrancher « 9 » cela revient à retrancher « 10 » et ajouter  « 1 »

Exemple : 57 - 9 = ( 57 – 10) + 1 = 47 +1 = 48.

Le chiffre des dizaines a diminué de « 1 » et le chiffre des unités a augmenté de « 1 ».

Compléter :

43 - 9 =

58 – 9 =

352 – 9 =

· 39 = 40 – 1

62 – 39 = ( 62 – 40) +1 = 22 + 1 = 23 Compléter :

73 – 19 =

54 – 49 =

143 – 59 =

378 – 299 =

653 – 109 =

2 728 – 999 =

Remarque : de la même façon : 72 – 28 = ( 72 – 30) + 2 = 42 + 2 = 44

Compléter :

100- 37 =

123 – 98 =

200 – 37 =

3°) MULTIPLICATION des entiers naturels

a )

En primaire , vous avons étudié la multiplication des nombres entiers et nous savons que .

Ainsi 7 5 = 35

« 35 » est le produit de « 7 » par « 5 »

« 7 » et « 5 » sont les facteurs du produit.

L’opération correspondante s’appelle la « multiplication » des entiers naturels.

b) Propriétés de la multiplication des entiers naturels.

· 7 1 = 7 et 1 5 = 5 ; « n » étant un entier naturel quelconque on a : n 1 = n On dit que « 1 » est élément neutre pour la multiplication des entiers naturels.

· 7 5 = 35 et 5 7 = 35 ; on constate alors que 7 5 = 5 7 Si l’on choisit d’autres entiers , on fera toujours la même constatation : «  on ne change pas la valeur du produit de deux entiers si l’on permute ces deux nombres ». On dit alors que la multiplication des entiers naturels est « commutative » . Cette propriété s’appelle la « commutativité » de la multiplication.

· 7 0 = 0 ; 5 0 = 0 ; « n » étant un entier naturel quelconque ; n 0 = 0 Si dans un produit, l’un des facteurs est nul,alors le produit est nul.

« On dira « que « 0 » est l’ élément absorbant de la multiplication »

c) Ordre de grandeur d’un produit :

Considérons le produit : 367 8 531 =

a) 300 < 367 < 400 et 8 000 < 8531 < 9 000

On peut dire que le produit de 367 8 531 est supérieur à 300 8 000 et est inférieur à 400 9 000

C'est-à-dire : 2 400 000 < 367 8 531 < 3600 000

Activités :

N°1 : Après avoir écrit les encadrements, donner un ordre de grandeur de 74 328 5 639

< 74 328 <

< 5 639 <

< 74 328 5 639 <

< 74 328 5 639 <

Un ordre de grandeur de < 74 328 5 639 < est :……………………………………………

N°2 : Sans faire d’encadrement, uniquement en considérant un ordre de grandeur de chaque facteur , donner un ordre de grandeur des produits suivants :

a = 38 4 39 2 146

Ordre de grandeur de « a » :

……………………………………………………..

b = 496 9 9 57

Ordre de grandeur de « b » :

……………………………………………………..

c = 123 497 3 075

Ordre de grandeur de « c » :

……………………………………………………..

N°3 :Dans chacune des lignes ci-dessous , une égalité est « vraie », les autres sont fausses. Sans effectuer la multiplication, trouvez la bonne égalité,encadrez –la (colorer la case)

43 5 4 = 9 3 22

43 5 4 = 2 3 22

43 5 4 = 20 3 22

23 00 470 = 1 081 000

23 00 470 = 1 08 100

23 00 470 = 1 81 000

825 224 = 18 480

825 224 = 84 800

825 224 = 184 800

d) Groupement de facteurs .

· Tu peux recommencer avec n’importe quels entiers, tu constateras toujours que le produit ne change pas si l’on place différemment les parenthèses. On dit alors que la multiplication des entiers est une opération « associative » . Cette propriété s’appelle l’associativité de la multiplication.

Exercice : Tu vas calculer : A = 7 4 5 3 en plaçant des parenthèses de différentes façons : 1°) Façon : A = ( 7 4 5 ) 3 effectuer le calcul : A = ( …….. ; 5 ) 3 ; A = ( 140 ) 3 ; A = ………

· Imaginer d’autres façons de placer les parenthèses puis effectue le calcul 2°) façon : A = 7 4 5 3 =……………………………………………………… 3°) façon : A = 7 4 5 3 =………………………………………………………

Décomposition de « 10 » ; « 100 » ; « 1 000 » en un produit de deux entiers.

· 10 = 2 5

· 100 = 10 10 = ( 2 5 ) ( 2 5 ) ; c'est-à-dire : 100 = 2 2 5 5

En groupant de divers façons ces 4 facteurs , trouver toutes les manières possibles d’écrire « 100 » sous forme d’un produit de deux entiers naturels.

Exemple : 100 = ( 2 2 ) ( 5 5 ) ; c'est-à-dire 100 = 4 25

· 1 000 = 10 10 10 = ( 2 5 ) ( 2 5 ) ( 2 5 ) ; c'est-à-dire 2 2 2 5 5 5

En groupant de divers façons ces 6 facteurs , trouver toutes les manières possibles d’écrire « 100 » sous forme d’un produit de deux entiers naturels.

Exemple : 1 000= ( 2 2 2) ( 5 5 5) ; c'est-à-dire 1 000 = 8 75 ; ou ( 5 5 )  ( 2 2 25) c'est-à-dire 1 000 = 25 40

· Pour calculer un produit, il est possible d’utiliser à a fois la commutativité et l’associativité afin de regrouper les facteurs dont le produit est un nombre se terminant par zéro.( on utilise les groupements étudiés précédemment)

Exemple :

B = 4 6 25 3 5 2

B = ( 4 25 ) ( 2 5 ) ( 6 3 ) ; ………. Poursuivez le calcul……(

B= ( 100 ) ( 10 ) ( 18 ) ; B = ( 1000 ) ( 18 ) = 18 000

Faire de même avec : C = 25 7 5 3 4 2

……………………………………………………………………………………………………

……………………………………………………………………………………………………

Faire de même avec : D = 125 7 25 6 4 5 8 2

……………………………………………………………………………………………………

……………………………………………………………………………………………………

TRAVAUX AUTO – FORMATIFS :

EVALUATION

.

Situations problèmes
N°1 : Une cuve à vin contient 2500 litres. ( l ) On soutire une première fois 557 l Une deuxième fois on soutire 824 l On en soutire encore une troisième fois . Il reste dans la cuve 800 l . Combien a-t-on soutiré de vin la troisième fois ?
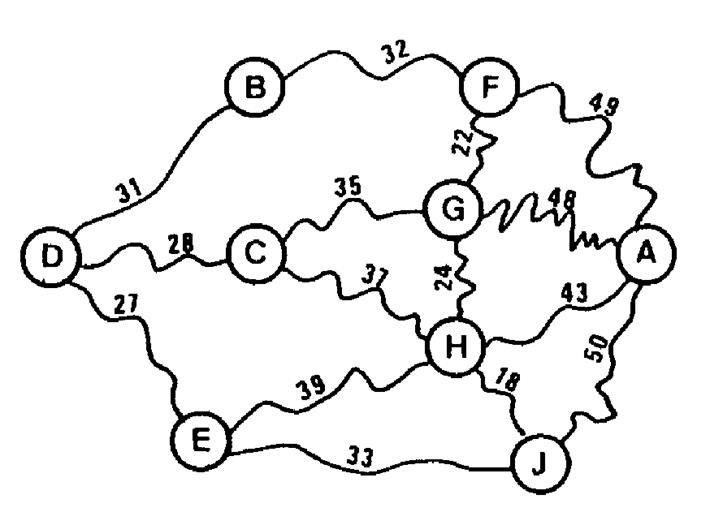
Voici , ci contre un extrait de carte . Les lettres dans les cercles représentent les villes. Les nombres sur les lignes indiquent la distance en km entre deux villes. Questions : 1. Trouvez le plus court chemin pour aller de « D » à « A ». Pour cela il faut calculer la longueur des différents parcours possibles. Exemple : Longueur du chemin « DBFA «  = 31 + 32 + 49 = 112
Problème n°3.
Multiplication :
Pb.1 : On veut planter des arbres fruitiers dans un jardin. Pour cela on achète 5 pommiers à 62 € l’un ; 3 poiriers à 73 € l’un , 2 pruniers à 84 € l’un et 4 cerisiers à 89 € . Quelle est la dépense ?
Pb2 : Caroline est née le 14 décembre 1975 à 9 h. le 14 décembre 1986 à 9 h , elle calcule le nombre de jours , puis le nombre d’heures qu’elle à vécu. Vous allez l’aider.* 1°) Calculez d’abord mentalement un ordre de grandeur du nombre d’heures . Vous trouvez ?........................................ 2°) Calculez le nombre de jours exact ,puis le nombre d’heures ( attention aux années bissextiles : 1972 ; 1976 ; 1980 ;1984 ;1988 )
Pb 3 : On veut numéroter les pages d’un cahier ayant 136 pages. 1°) Combien de chiffres devrez vous écrire en tout ? 2°) Combien de fois écrirez vous le chiffre « 1 » ?
Pb4 : 5 enseignants se rencontre à 7 h 50 mn en salle de professeurs, ils se saluent et chacun serre la mian de ses autres collègues. Combien y a – t-il en tout de poignées de mains. ?
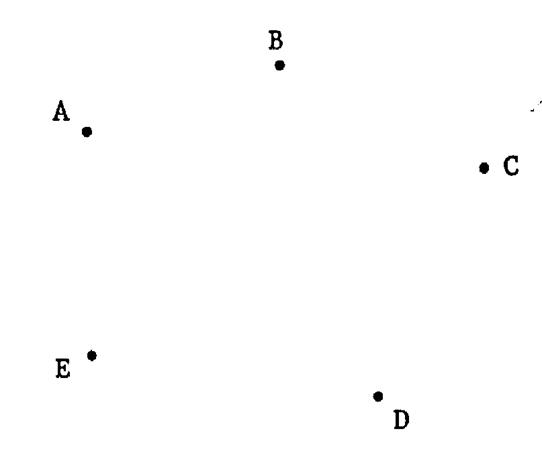
Voici cinq points « A » ; « B » ; »C », »D » et « E ». 1°) On trace toutes droites possibles contenant deux de ces points. Combien en tracez vous ? 2°) Retrouvez ce nombre par le calcul.