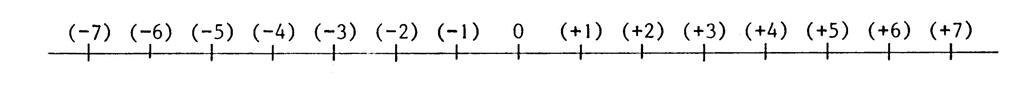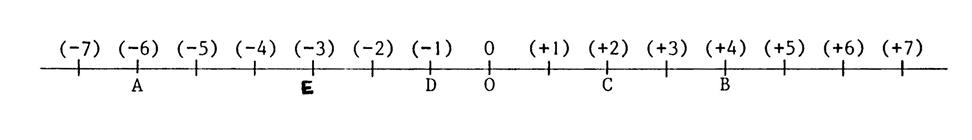les nombres décimaux_repérage sur une droite... au collège_corrigé du document

DOSSIER : LES DECIMAUX non - relatifs / objectif cours 12

6ème  Collège.

INFO prof :  Tout exercice sur les nombres relatifs donné sous la forme :  3 – 7 ;ou ;  3 + 7  est faux ; parce que « trois » est la valeur absolue de deux nombres relatifs opposés . 

 « 3 »  n’est pas la forme simplifiée du nombre relatif  +3  ( voir le  cours ) .

Pré requis :

Le nombre décimal

Retour vers la fiche à travailler.

Les nombres positifs ou négatifs ; dits aussi « algébrique » :

 

ENVIRONNEMENT du dossier:

Index warmaths :

Objectif précédent :

·       L’abscisse d’un nombre décimal

 

·       Le nombre relatif ( généralités)

Objectif suivant :

1°) les rationnels

2°)Les nombres réels

3°)calcul algébrique :la valeur absolue

4°) Le nombre décimal relatif (suite)

Info générales.

1°) INFORMATIONS sur les nombres décimaux relatifs.

2°) tout sur Le calcul numérique.

3°) Cours sur le repérage.

 

  Corrigés des Activités découvertes sur  LES NOMBRES RELATIFS (entier ou décimal)

 

1°)  Comment justifier l’écriture « normalisée » d’un nombre relatif…( voir les 3 exemples qui conduisent à la forme normalisée)

 

 

2°) Les nombres entiers relatifs.

 

 

3°) La droite graduée- repérage d’un nombre relatif.

 

 

 

 

 

Test      FilesOfficeverte

COURS :                 FilesOfficeverte

Devoir  Contrôle FilesOfficeverte

Devoir évaluation FilesOfficeverte

           Application             

 

Corrigé Contrôle  FilesOfficeverte

Corrigé évaluation  FilesOfficeverte

 

Exemples d’énoncés d’opérations n’entrant pas dans le cadre des opérations avec des nombres relatifs :

12 + 6,5  =

14,5 – 28,3 =

2,3 4,65

( -3,5)  1,5

2,7  ( - 8) =

95 : 4

5,2 : ( + 2,6)

 ( -3,8) : 4

12 ; 6,5 ; 14,5 ; 2,3 ; 4,65 ; 1,5 ; 2,7 ; 95 ; 4 ; 5,2 ;4 ne sont  pas des décimaux relatifs positifs ! ! ! ! ! !

 

COURS

 

 

 

 

1°)Des exemples : Comment justifier l’écriture « normalisée » d’un nombre relatif…

 

 

Exemple 1 :

 

 

 

 

 

 

Ci-contre on vous donne ,une droite « x y » . Sur cette droite on a placé un point zéro.

·       Placez un point à 5 cm de « O ».

( vous vous rendez compte que vous pouvez placer ce point en deux endroits différents……)

yreperage_gradua_1x

 

 

On  reprend l’activité précédente en vous apportant une autre précision …..:

On vous demande de placer sur une droite « x y » deux points  situés à « 5 cm » du point « O ».

reperage_gradua_2

L’un s’appelle « M » et l’autre « M’ »

Vous constatez  alors qu’au seul  nombre de « 5 » correspondent deux points. 

Aussi , pour les différencier, il faut une indication complémentaire.

 

 

 

En plus de la distance : « 5 » , il faut donc préciser, par exemple

·       si le point est à droite ou à gauche du point « O » ou

·        si la droite est « verticale » de préciser si le point est  au- dessus ou en dessous du point « O »    ( c’est le cas d’un  thermomètre à alcool  !!) .

On pourrait « coder » la position de ces points sur la droite tel que :

·       Si La droite est horizontale : pour le point à gauche de « O »  on note «  5 G »  et  pour le point à droite ( 5G)

·       Si la droite est verticale : pour le point au -dessus du point « O » on note «  5 H »   et pour le point sous le point « O » « 5 B »

 

Activité 1  :

Sur la droite ci-dessous placez les points : 5 D ; 5G ; 3 D ; 6 G

 

 

 

reperage_gradua_1

 

 

Exemple 2 :

 

 

Des enfants jouent aux billes. A la fin de la partie, ils font leurs comptes.

Paul a maintenant 16 billes, au début il en avait 10 .  Il a gagné (g) … 6 …  billes . Ce que l’on peut coder par « 6g ».

Victor a maintenant 14 billes, au début il en avait 25 .  Il a perdu  (p) …9 …  billes . Ce que l’on peut coder par « 9p ».

 

Comme dans l’exemple précédent, pour représenter la situation, « 6 » ou « 9 » ne suffisent pas.

Il faut une indication complémentaire qui explique la situation « gain (g) »   ou  « perte  (p)».

 

 

 

Activité 2 :

Complétez le tableau ci-dessous.

 

 

 

Paul

Victor

Simon

Pierre

Julien

Benoit

Mathieu

Raymond

 

Nombre de billes

« à la fin »

16

7

23

0

17

6

26

13

« au début »

12

22

14

11

17

17

11

17

« Gain (g) » ou « perte (p)»

4 g

15 p

9g

11p

0 g 0 p

11 p

15 g

4 p

 

 

 

 

Exemple 3 :

 

 

On vous propose de jouer :

On met a votre disposition un sac de jetons.

Ces jetons sont « jaune » ou « vert ». Sur chaque jeton est inscrit un nombre.

Vous possédez un pion que vous pourrez placer dans les cases de la bande reproduite ci-dessous. (la case  sombre est la case de départ).

 

 

 

 

7g

6g

5g

4g

3g

2g

1g

0g-0d

1d

2d

3d

4d

5d

6d

7d

 

 

 

Vous plongez la main dans le sac et vous en tirez un jeton . Si le jeton est  jaune il indique un déplacement vers la droite , s’il est vert il indique un déplacement vers la gauche.

Par exemple : vous tirez le jeton « 4 » jaune. Votre pion étant au départ , vous le déplacez de 4 cases vers la droite. La nouvelle position du pion peut se coder « 4 d »  .

Si vous aviez tiré le jeton « 3 vert », votre pion étant sur le point de départ , vous l’auriez déplacé de 3 cases vers la gauche.. Cette position pourrait être codé «  3 g » .

Nota : il existe un jeton jaune et  un jeton vert qui porte le nombre « 0 ».

Si vous tirez l’un de ces jetons , partant toujours de la case départ, où placerez-vous ce pion ?             Cette case peut alors être codée  «  O d »  ou « O g ».

 

Activité 3  :

Sur la bande ci-dessus, écrivez le code de chaque case.

 

 

2°) Les nombres entiers relatifs.

 

 

 

Dans les exemples du « 1 » , pour coder une situation déterminée , on a utilisé un nombre entier et une indication ( à 2 possibilités) .

 

 

Cette indication complémentaire étant :

Exemple 1 : en haut et en bas.

 

Exemple 2 : « gain » et « perte »

Exemple 3 : « à droite » et « à gauche »

 

On peut uniformiser les notations en choisissant un même symbole  pour représenter ces situations. Ce symbole est appelé « le signe » .

On utilisera , par exemple :

 

 

 

«  + »     (plus) pour « en haut  (h) » , « gain (g)» , « à droit (D)» .

 

 

«  - »     (moins) pour « en bas (b) » , « perte (p) » , « à gauche (G)» .

 

Ainsi :

 

 

« 17 h » se notera  ( + 17)

« 9 p» se notera ( - 9 )

« 5 D » se notera ( + 5 )

 

« 17 b »  se notera ( - 17 )

«  6 g » se notera ( + 6 )

«  2 G » se notera ( - 2 )

 

v  

 

 

 ( + 17 ) ; ( - 9 ) ; ( + 5 ) ; ( - 21 ) sont des nombres appelés « entiers relatifs ».

 

 

( + 5 ) ; ( + 47 ) ; ( + 587)  sont des entiers relatifs positifs , leur signe est « + » ; on dit que  la valeur « absolue »  est précédée du signe « + ».

( - 5 ) ; ( - 47 ) ; ( - 587)  sont des entiers relatifs négatifs , leur signe est « -» ; on dit que  la valeur « absolue »  est précédée du signe « - ».

« 0 » est à la fois « positif » et « négatif ».

 

 

 

Vous voyez que deux nombres relatifs  peuvent  être composés avec les mêmes chiffres,  exemple  ci-dessous « 5 » ; on dira qu’ils ont la même « valeur absolue »…….

 

 

reperage_graduat_3

 

 

 

 

 

3°) La droite graduée.

 

 

Nous reprenons l’exemple « « «  du chapitre « 1 »

 

 

 

7g

6g

5g

4g

3g

2g

1g

0g-0d

1d

2d

3d

4d

5d

6d

7d

 

 

 

On remplace les « g » par le signe « - »   et le signe « d » par le signe « + »………..

 

 

 

 

-7

- 6

- 5

- 4

- 3

- 2

-1

0

+ 1

+ 2

+ 3

+ 4

+ 5

+ 6

+ 7

 

 

 

 

 

 

Au lieu de placer les entiers relatifs dans des cases, on peut utiliser une droite graduée comme on l’a fait au chapitre sur les « entiers naturels ».

 

 

 

 

reperage_002

 

 

En imaginant que cette graduation est illimitée des deux côtés, on obtient une « représentation graphique »  de l’ensemble des nombres entiers naturels. »

 

 

v On a ainsi fait correspondre à chaque point de la graduation un entier relatif.  ( ci-dessous on a fait correspondre des noms (lettres)  à certaines graduations)

 

 

reperage_001

 

 

à   « B » on a fait correspondre l’entier relatif ( + 4 )

à   « A » on a fait correspondre l’entier relatif : ……( - 6 )

 

à   « C » on a fait correspondre l’entier relatif ( + 2 )

à   « E » on a fait correspondre l’entier relatif ( - 3 )

à   « D » on a fait correspondre l’entier relatif ( - 1 )

à   « O » on a fait correspondre l’entier relatif : ( + 0 ) ou ( - 0 )

 

 

 

 

v  Le nombre correspondant au point est appelé «  l’abscisse du point » ….

 

 

à   « B » on a fait correspondre l’abscisse  ( + 4 )

à   « A » on a fait correspondre l’abscisse: ……( - 6 )

 

à   « C » on a fait correspondre l’abscisse ( + 2 )

à   « E » on a fait correspondre l’abscisse ( - 3 )

à   « D » on a fait correspondre l’abscisse ( - 1 )

à   « O » on a fait correspondre l’abscisse: ( + 0 ) ou ( - 0 ),  

Le point « O » est appelé l’origine de la graduation.

 

 

 

 

v On peut alors subdiviser les graduations de la droite des entiers relatifs…..

 

 

On obtient  des points qui ont pour abscisses des décimaux relatifs…..

 

 

reperage_graduation_point001

 

 

Activité 4  :

 

 

Placez les points  «  R » , « S » , « T » d’abscisses respectives :   ( + 6) , ( - 2) , ( - 5 )

 

 

v Ci-dessous, on vous donne une droite graduée :

L’abscisse de « G » est ( + 2,6 )

 

 

reperage_graduation001

 

 

Activité 5  :

 

 

L’abscisse de « K » est ( - 1,5 )

L’abscisse de « H » est ( + 0,4 )

L’abscisse de « L » est ( - 0, 8 )

 

 

 

 

 

Remarque il est bien entendu que l’on peut avoir à faire à des nombre tels que : ( - 15,7) ; ( + 67,8) ; ( - 6, 047) ; ….

 

 

 

 

 

Activité 6  :

 

 

Placez les points  T ; D ; Q  d’abscisses respectives  ( - 2,2) ; ( + , 1,9) ; ( - 3,3 )

 

 

 

 

 

 

 

 

 

 

 

 

 

 

TRAVAUX AUTO  FORMATIFS.

 

 

 

« CONTROLE »:

 

              1°) Comment reconnait-on  un nombre relatif ?    Combien de parties comporte un nombre relatif?  (précisez)

                          

   « EVALUATION »

 

      1°)   Nommez les trois  parties principales de   (+3)

      2°) Faire les activités proposées en devoir.