|
Leçon |
Titre |
|
N°2 |
CORRIGE des TRAVAUX d’ AUTO -
FORMATION sur FRACTIONS – ECRITURE FRACTIONNAIRE - DUREE. |
Compléter les phrases suivantes :
1°) Fraction :
Il y a « fraction » ; si les deux nombres séparé par une barre
sont des nombres entiers .
Le nombre en dessous du trait
de fraction appelé : dénominateur indique en combien de parties égales on divise
une quantité ( appelé :
Unité)
Le nombre au dessus du trait de fraction appelé numérateur indique combien on prend de ces parties .
2°) Ecriture décimale d’une fraction :
a)
Ecriture décimale d’ une fraction décimale : Lorsque le
dénominateur d’une fraction est
10 ; 100 ; 1000 ; …., nous avons ce que l’on appelle une fraction décimale :elles
peuvent s’écrire sous forme d’une écriture décimale .
Une
fraction est décimale si dans la division
le quotient est exact.
b)
Ecriture décimale d’une fraction non – décimale :
Une fraction
est dite « non – décimale » si
la division ne tombe pas juste .( le quotient n’est pas exact )
La valeur décimale représentant
la fraction non décimale est le quotient
arrondi . On séparera la fraction et la valeur
décimale arrondie par le signe « » » qui se lit « peu
différent de …. »
3°)
fractions égales :
Des
fractions sont égales si elles ont la même écriture décimale .
Si on
multiplie le numérateur et le dénominateur d’une
fraction par un même nombre , on obtient une fraction égale .
Si on
divise le numérateur et le dénominateur d’une
fraction par un même nombre , on obtient une fraction égale
.Dans ce cas ,on dit que l’on simplifie la
fraction .
Un fraction est irréductible
si elle ne peut plus être simplifiée.
4°) Multiplication d’une fraction par un
nombre :
citer les deux procédures que l’on peut utiliser pour
multiplier une fraction et un nombre .
1ère
possibilité : Pour prendre la fraction d’un nombre on fait le produit de
ce nombre par le numérateur de la fraction , puis on
divise le résultat par le dénominateur. .
2ème
possibilité : Pour multiplier une fraction par un nombre
, on fait le produit de la valeur
décimale de la fraction par ce nombre .
5° ) Calcul de
durée ( système sexagésimal)
a)
Comment procède - -t – on pour passer
une durée exprimée en valeur sexagésimale en durée
exprimée en valeur décimale ?
Pour
exprimer une durée
dans le système décimal
en prenant l’heure pour unité , on divise le nombre de
minutes par 60 .
b)
Comment procède - -t – on pour passer
une durée exprimée en valeur décimale en durée
exprimée en valeur sexagésimale ?
Pour
exprimer la durée exprimée dans le système décimal dans le système sexagésimal , on
multiplie la partie décimale par 60 pour obtenir le nombre de minutes.
|
CORRIGE : TRAVAUX N°2 d ’ AUTO - FORMATION :
EVALUATION: |
Exercices :
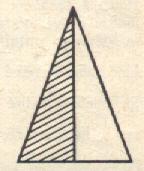
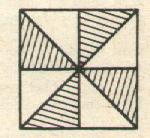
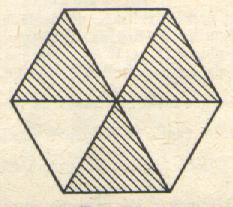
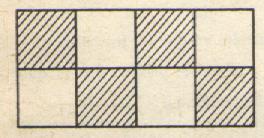
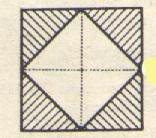
1°) La fraction : hachurées couvre la moitié de l’aire totale (A) . ( 0,5 A)
|
0,5 = |
0,5 = |
|
|
|
|
0,5 = |
0,5 = |
|
|
|
|
0,5 = |
0,5 = |
|
|
|
2°) Ecriture décimale d’une fraction :
Donner la valeur
décimale des fractions suivantes ( arrondir les valeurs à 0,001 prés si nécessaire)
|
|
Résultat |
|
|
Résultat |
|
|
0,500 |
|
|
0,625 |
|
|
0,250 |
|
|
1,750 |
|
|
0,333 |
|
|
0,667 |
|
|
0,75 |
|
|
0,600 |
|
|
0,600 |
|
|
0,846 |
|
|
0,500 |
|
|
0,667 |
3°)Fractions égales :
série 1 : Trouver des fractions égales ; dont le
dénominateur est 100.
|
|
Résultat |
|
|
Résultat |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
impossible |
|
|
|
|
|
|
|
|
|
Série 2 :Simplifier les fractions suivantes :
|
|
Résultat |
|
|
Résultat |
|
|
|
|
|
On divise par 3 : |
|
|
On divise par 2 ;
|
|
|
On divise par
2 ; |
|
|
On divise par 3 ;
|
|
|
*On divise par 2 : |
Série 3 : compléter les fractions
suivantes :
|
|
Fraction : |
|
|
Fraction : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4°) Multiplication d’une fraction par un nombre : ( Voir le cours sur
les opérations avec des fractions)
série 1 : effectuer les opérations
suivantes puis simplifier le résultat :
|
|
|
|
|
|
|
|
Série 2 : Compléter le tableau : faire le calcul ( multiplication ) ,
donner le résultat sous forme de
fraction , ensuite sous forme
décimale ( à 0,01 prés)
|
´ |
2630 |
1240 |
1374 |
473 |
|
|
|
744 |
824,4 |
283,8 |
|
|
1502,86 |
708,57 |
785,14 |
270,29 |
|
|
*1533,33 |
826,67 |
916 |
315,33 |
|
|
1820,77 |
858,46 |
951,23 |
327,46 |
5° La durée :
Convertir les durées suivantes ( arrondir à la minute près ; ou au 0,01 )
|
Heures ,
centièmes |
Minutes |
Heures , minutes
|
|
2,25 |
135 |
2 h 15’ |
|
12,66 |
759,6 ‘
ou 759’ 36’’ |
12 h 39’ 36’’ |
|
4,4166667
soit environ 4,42 |
265’ |
4 h 25 min |
|
39,166667 h soit environ 39,17 |
2350 |
39h 10’ |
|
0,86 |
51’36’’ |
51’36’’ |
|
1,9166667 h soit environ 1,92 |
115’ |
1h 55 min |
PROBLEMES :