TESTS niveau V

=Savoir résoudre une équation du premier degré à une inconnue de la forme : ax = b ; a + x = b ; x - a = b et ax + b = c =Résoudre un problème avec une des équations pré - citées.

TESTS aller chercher la réponse dans le corrigé	LECON :
N°11	Résoudre une équation du premier degré et PROBLEMES DU PREMIER DEGRE

CONTROLE:

1°) Donner la définition de «  Equation du premier degré . à une inconnue »:

2°) Que signifie "résoudre" une équation du premier degré à une inconnue ?

3 °) Donner la solution de l’équation

L'équation a x = b  ; à pour solution :

L'équation a x + b = c : ; à pour solution :

5°) Donner la procédure permettant de résoudre un problème du premier degré .

EVALUATION:

1°) Résoudre les exercices suivants : (le corrigé est dans le cours)

N°	Exercice	Résultat :	note
1	7 x = 63
2	5 x = 45
3	13 + x = 45
4	9 x - 5 = 4
5	2x -11 = 45
10	7 - 5x = 23
11	13 - x = - 71
12
13
14

Problèmes: On demande :d’identifier l’inconnue , d’écrire une équation et de résoudre l’équation. (vous aider d’un dessin éventuellement)

N°1 Le réservoir d'une voiture est au deux cinquièmes rempli . Il faut ajouter 38 litres de carburant pour le remplir entièrement . Quelle est la contenance de ce réservoir ?

N°2 Le réservoir d'un voiture est vide aux deux tiers . On ajoute 30 litres de carburant pour le remplir aux trois quarts . Quelle est la contenance du réservoir ?

N°3 la largeur d'un rectangle est le tiers de sa longueur et le périmètre mesure 48 m . Calculer les dimensions de ce rectangle . ( 6 et 18 m)

N°4 La longueur d'un rectangle surpasse de 10 m sa largeur . Le périmètre est de 120 m .Calculer les dimensions de ce rectangle . ( 25 et 35 m)

N°5 Un centre de formation organise un voyage .Le transporteur propose un prix global correspondant à 160 € par personne . Si le nombre de personnes augmente de 5 , on passe pour le même prix global , à 120 € par personne.

Combien de personnes participent au voyage ?

N° 6

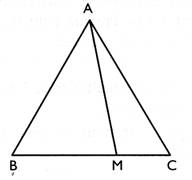
ABC est un triangle équilatéral de côté 6 cm On place sur le côté [BC] le point M tel que BM = d. 1°) calculer la hauteur du triangle ABC , puis l'aire du triangle . 2) où doit -on placer le point M pour que l'aire du triangle AMC soit égal à 10?

N°7

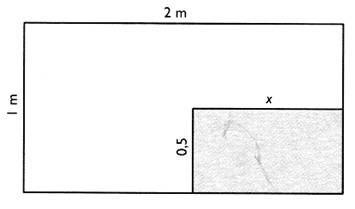
Dans une pièce rectangulaire de 2 m de longueur et de 1 m de large , on effectue une découpe de forme rectangulaire comme l'indique la figure ci -dessous.

Donner l'expression de l'aire de la partie restante en fonction de "x".

Calculer "x" pour que l'aire de la partie restante soit 1,25 m² .

N° 8

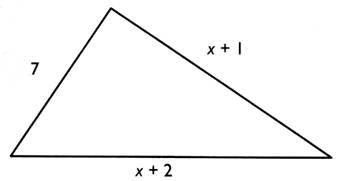
Un triangle a les dimensions ( en m) indiquées sur la figure . Exprimer le périmètre du triangle en fonction de "x". Calculer "x" pour que le périmètre soit égal à 30 m . En déduire les dimensions du triangle .

N°9

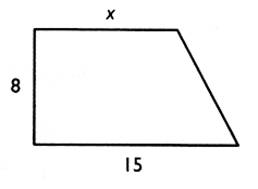
Montrer que l'expression de l'aire du trapèze rectangle en fonction de "x" est : A = 4 x + 60 Calculer "x" pour que l'aire du trapèze rectangle soit égale à 200 cm² . Pour cela , résoudre l'équation : 4x + 60 = 200