|
Leçon |
|
|
N°11 |
TRAVAUX d ’ AUTO
- FORMATION sur Résoudre une équation du
premier degré et PROBLEMES DU PREMIER DEGRE |
|
|
a) Donner
la définition d ’ une
« équation »
Une
équation algébrique possédant une inconnue ( "x"
généralement ) est une égalité qui n'est pas vraie pour n'importe quelle valeur
donnée à cette inconnue
b) Donner
la définition d ’ une « équation du premier degré »
Une
équation du premier degré possède un ou plusieurs termes contenant une ou plusieurs inconnues dont la puissance n’ est pas supérieur
à « 1 » .
c) Donner
la définition d ’ une « équation du premier degré à une
inconnue »:
Une équation du premier degré à une inconnue est
une égalité dont un ou plusieurs termes contient une seule
et même lettre ( appelée : inconnue) et dont
on affecte « normalement »
l’exposant « 1 » , on dit que
l’inconnue est de puissance 1 .
Informations
complémentaires :
Ainsi
le terme « 2 x » devrait s’écrire « 2x 1 » ; par
convention d’écriture , au lieu d’écrire
« 2 x 1 » on
écrira « 2x ».( Si la puissance « 1 » n’est pas indiquée, il ne faut pas oublier qu’elle existe tout de même ).
On ne doit
pas confondre « x0 et x1
» parce que toute écriture
de la forme x0 est
égale à
« 1 » et que toute écriture de la forme x1 est égale à « x »
Exemples : 9 0 =
1 ; 9 1 = 9
d) Que
signifie : « Résoudre une équation »
Résoudre
une équation du premier degré à une inconnue c’est rechercher par
transformation et calcul la valeur de l’inconnue qui vérifie l’égalité vraie.
2°) Définition
« membre ; terme ; facteur » .
Compléter les phrases
suivantes :
a) Dans une égalité l’expression algébrique à gauche
du signe « égal » est appelé « premier
membre » .
b) Dans une égalité l’expression algébrique à
droite du signe « égal » est
appelé « deuxième membre » .
c) Dans une
équation ,
le signe " = " sépare les deux "membres".
a) Terme : un terme
est composé de un ou plusieurs facteurs .
e)
Facteur : un facteur est un nombre ou une lettre situé à gauche et à droite du
signe ´
( on dit
qu’un terme est constitué d’un produit de facteurs
)
3°) Que signifie
"résoudre" une équation du premier degré à une inconnue ?
Résoudre une équation du premier degré à une inconnue c'est
rechercher la valeur de « x » qui vérifie l’égalité numérique vraie .
Cette transformation conduit à une
égalité de la forme « a x = b » , le calcul de « b / a » permet
d’obtenir cette valeur de "x" . Cette valeur trouvée
, remplacée dans l’équation de départ , doit vérifier que l'égalité numérique est "vraie".
4 °) Compléter les phrases
suivantes :
Série
1 :
a) L'équation
du type a x = b :
les mots manquants sont : « solution unique x = ![]() » ; « décimaux » ;
« 0 » ; « on divise »
» ; « décimaux » ;
« 0 » ; « on divise »
b)L'équation du type a x = b ( "a" et "b" sont des
nombres décimaux et "a" ¹ 0) admet une solution unique x = ![]()
c) Cette
solution est obtenue par une seule opération : on
divise les deux membres de
l'égalité par le même nombre "a" .
d)L'équation du type a x+ b =
c
Série 2 : les mots manquants sont
: « 0 »; « décimaux » ;
« unique » ; « divise » ;
« deux » ; « l'opposé de "b" » ;
« a » ; « de membre il change de signe » ;
e)L'équation du type a x+ b =
c ( "a" , "b" et
"c" sont des nombres décimaux et
"a" ¹ 0)
admet une solution unique )
b)
Cette solution est obtenue par deux opérations :
![]()
g)On ajoute aux deux membres l'opposé de
"b" . On dit que : si « b » change de membre il change de signe.
h) on divise les deux
membres de l'égalité par le même nombre "a" .
5°) Donner la procédure permettant
de résoudre un problème du premier degré .
Pour résoudre un problème , on doit
respecter l'ordre de procédure suivant :
a)
Choix de la ou des inconnues : recherche de l'inconnue : après avoir lu et analysé
l'énoncé , choisir une inconnue .
b)
Mise en équation : établir l'
équation traduisant la situation étudiée .
c)
Résolution de équation , ou d’un système d’équations du premier degré
à 1 ou 2 inconnues .
d)
Discussion du problème :
énoncer le résultat en rédigeant
une phrase et vérifier si ce résultat est conforme au problème posé .
|
TRAVAUX N° 11
d ’ AUTO - FORMATION : EVALUATION: |
|
1°)
Entourer l’équation les premiers
degrés :
x ²+ 3 = 0 ; x + 3 = 0 ; 2y²
+ 5 = 0 ; 2x + - y - 4z = 15 ; x y = 6z ; x - y = 6z ; 2y + 5 = 0 ; 2x + - y - 4z² = 15 ;
![]() x + y = 18 ;
x + y = 18 ;
2°)
Entourer les équation du premier degrés à une inconnue
.
x ²+ 3 =
0 ; x +
3 = 0 ; 2y² + 5 = 0 ; 2x + - y - 4z = 15 ; x y = 6z ; x - y = 6z ; 2y + 5 = 0 ; 2x + - y - 4z² = 15 ;
x² y = 6z ;
3°) Entourer le premier membre :
x - y =
6z ; x + 3 = 0
4°)
Entourer le second membre .
2y² + 5 = 0 ; 2x + - y =
- 4z + 15
5°) Entourer les termes .(
transformer les expressions en sommes
algébriques )
|
Expression : |
Somme
algébrique |
Facteurs : |
|
x + 3
= 0 |
( x ) + + 3)
= 0 |
( x ) et (+ 3) |
|
2x - 8 =
- 4x + 15 |
(+2x) + (- 8 )= (- 4x) + ( + 15) |
(+2x) ; (- 8 ) ; (-
4x) ;(+15) |
6°)
Résoudre les exercices suivants : (le corrigé est dans le cours)
|
N° |
Exercice |
Résultat
: |
|
|
1 |
1 x
= 7 |
x = 7 |
™ |
|
2 |
5 x =
45 |
x = 9 |
™ |
|
3 |
5+ x = 45 |
x = 40 |
™ |
|
4 |
5 - x =
45 |
x = - 40 ( 5 = 45 + x ; x =
5 - 45 ; …) |
™ |
|
5 |
x -5 = 45 |
x = 50 |
™ |
|
6 |
|
x = 15 ;
(2 x = 3 0) |
™ |
|
7 |
|
x = 5/3 ;
(10 = 6 x ) |
™ |
|
8 |
|
x = 15 ; ( 30 = 2x
) |
™ |
|
9 |
|
x =5/3 ; (6 x = 10) |
™ |
|
10 |
|
x = 40 |
™ |
|
11 |
|
x = ; 5
= 2x ;
x = 2,5 |
™ |
Exercices (suite)
Résoudre
les équations suivantes ( l'inconnue est la lettre , si nécessaire , arrondir le
résultat à 0,01 près .)
Série :1
|
|
Exercices |
Résultat |
Note |
|
1 |
6x = 54 |
x =
9 ; ( 54 / 6 ) |
Ÿ |
|
2 |
2x = 6,5 |
x = 3, 25
; ( 6,5
/2 ) |
Ÿ |
|
3 |
7x = 84 |
x = 12
; ( 84
/ 7 ) |
Ÿ |
Série : 2
|
|
Exercices |
Résultat |
Note |
|
1 |
1,1 x = -
143 |
x = - 130
; ( 143
/ 1,1 ) |
Ÿ |
|
2 |
4 x = 2,4 |
x = 0, 6
; ( 2,4 / 4 ) |
Ÿ |
|
3 |
3x = 3,81
|
x = 1,27
; ( 3,81 / 3 ) |
Ÿ |
Série : 3
|
|
Exercices |
Résultat |
Note |
|
1 |
24 z = - 9,6 |
z = - ( 9,6 /24) = - 0,4 |
Ÿ |
|
2 |
3 z =
26,1 |
z = 26,1 / 3 |
Ÿ |
|
3 |
7,1 z =
435,2 |
z = 435,2 / 7,1 |
Ÿ |
Série : 4
|
|
Exercices |
Résultat |
Note |
|
1 |
X+ 3 = 7 |
x = 7 - 3 ; x = 4 |
Ÿ |
|
2 |
X + 13 =
21 |
x = 21 - 13 ; x = 8 |
Ÿ |
|
3 |
X + 18 =
6 |
x = 6 - 18 ; x =
- 12 |
Ÿ |
Série : 5
|
|
Exercices |
Résultat |
note |
|
1 |
X+ 23 = 0 |
X = - 23 |
Ÿ |
|
2 |
X - 11 =
0 |
X = 11 |
Ÿ |
|
3 |
X + 2,13
= 0,3 |
X = 0,3 - 2,13 ; x = 1,83 |
Ÿ |
Série : 6
|
|
Exercices |
Résultat |
note |
|
1 |
-x + 7
= 2 |
7 = x +2 ; x = 7 - 2 ; x = +5 |
Ÿ |
|
2 |
- x + 3 =
5 |
- x + 3 = 5 ; + 3 = 5 + x ; 3 - 5 = x ; x = -2 |
Ÿ |
|
3 |
-2 - x =
6 |
-2 - x = 6 ; -2 - 6 = x ; x = -8 |
Ÿ |
Série : 7
|
|
Exercices |
Résultat |
note |
|
1 |
3x + 15 =
25 |
3x = 25 - 15 ; 3x
= 10 ; x =
10 /3 |
Ÿ |
|
2 |
2x + 6 =
13 |
2x = 13 - 6 ; 2x = 7 ; x
= 3,5 |
Ÿ |
|
3 |
7x + 67 =
89 |
7 x = 89
- 67 ; 7x = 22 ; x = 22 / 7 |
Ÿ |
Série : 8
|
|
Exercices |
Résultat |
note |
|
1 |
5y - 3 =
7 |
5y = 3 + 7 ; 5 y =
10 ; y = 2 |
Ÿ |
|
2 |
2y + 3 =
1 |
2y = 1 -3 ;
y = -1 |
Ÿ |
|
3 |
12 y -
62= 14 |
12 y = + 62 + 14 ; 12 y
= 76 ; y » 6,33 |
Ÿ |
Série : 9
|
|
Exercices |
Résultat |
note |
|
1 |
4x - 32 =
0 |
4x = 32 ; x = 8 |
Ÿ |
|
2 |
2 x +2,4
= 0 |
2 x = - 2,4 ; x = - 1,2
|
Ÿ |
|
3 |
0,3 x -
2,1 = 0 |
0,3 x = + 2,1 ; x = 7 |
Ÿ |
Série : 10
|
|
Exercices |
Résultat |
note |
|
1 |
6x - 5 =
4 |
6x = 5 + 4 ; 6 x =
9 ; x = 9 / 6 ; x = 1,5 |
Ÿ |
|
2 |
0,3 x + 1
= 1,9 |
0,3 x = - 1 + 1,9 ;
0,3 x = 0,9 ; x = 0,3 |
Ÿ |
|
3 |
5x - 5 =
- 32 |
5x - 5 = - 32 ; 5 x = - 32 +5 ; 5x = -27 ; x = 5,4 |
Ÿ |
Série : 11
|
|
Exercices |
Résultat |
note |
|
1 |
- 1,3 x + 4,1 = 0 |
4,1 = 1,3 x ; x » 3,15 |
Ÿ |
|
2 |
- 17,4 x
+ 53,2 = 3,1 |
53,2 - 3,1 = 17,4
x ; 50,1 / 17,4 = x ; x » 2,88 |
Ÿ |
|
3 |
0,4 x -
1,2 = 0 |
0,4 x = 1,2 ; x = 1,2 / 0,4 |
Ÿ |
Série : 12
|
|
Exercices |
Résultat |
note |
|
1 |
|
0,3 fois x = 21 fois 1,2 ; 0,3 x = 25,2 ; x = 84 |
Ÿ |
|
2 |
|
2,5 fois 17 = 8,5 fois x ;
8,5 x = 42,5 ; x = 5 |
Ÿ |
Série : 13
|
|
Exercices |
Résultat |
note |
|
1 |
|
X = 15 |
Ÿ |
|
2 |
|
3x = 18 ; x = 6 |
Ÿ |
|
3 |
|
|
Ÿ |
Série : 14
|
|
Exercices |
Résultat |
note |
|
1 |
|
18 x = 20 ; x = 20/18 |
Ÿ |
|
2 |
|
6 ( x
+ 4 ) = 3 fois 2 ; 6 x + 24 =
6 ; 6x = -18 ; x = - 3 |
Ÿ |
|
3 |
|
x + 3 = 24 ; x = 21 |
Ÿ |
|
4 |
|
2x - 3 = 4,2 fois 5 ;
2x - 3 = 21 ; 2x =
24 ; x = 12 |
Ÿ |
Problèmes
( traités dans le cours)
Enoncé 1
: On achète 3
kilogrammes de fruit à 3,75 € . Quel est le prix d' un kilogramme de
fruit ?
On
demande :
Identifier
l’inconnue .
Ecrire
une équation .
Résoudre
l’équation.
Conclure .
Résolution :
On pose "x" le prix du kilogramme de
fruit.
Cela nous donne l'équation 3 x = 3,75
On divise les deux membres par "3": ![]() =
= ![]()
D'où x
= 1,25
Conclusion : le prix d'un kilogramme de fruit est de
1, 25 €
Enoncé
N°2 On achète 3 kilogrammes de fruit , je donne
un billet de 5 € , la caissière
me rend 0,2 € .Quel est le prix d' un kilogramme de fruit ?
On
demande :
Identifier
l’inconnue .
Ecrire
une équation .
Résoudre
l’équation.
Conclure .
Résolution :
On pose "x" le prix du kilogramme de
fruit.
Cela nous donne l'équation 3 x +
0,2 =
5
On joute
"- 0,2" dans chaque membre :
3 x +
0,2 - 0,2 =
5 - 0,2
3 x = 4,8
On divise les deux membres par "3": ![]() =
= ![]()
D'où x
= 1, 60
Conclusion : le prix d'un kilogramme de fruit est de
1, 60 €
N°3: : Un rectangle a les
caractéristiques suivantes :
Son
périmètre mesure 80 m ; sa longueur est le triple de sa largeur .
Calculer sa longueur et sa largeur .
nommons "x" la largeur du rectangle . l = x
en fonction de "x" : la longueur du
rectangle est L = 3x
le demi - périmètre est : L + l = x
+ 3x
= x ( 1 + 3) = 4 x
le périmètre est =
2 fois le demi - périmètre : P =
2 ( 4x) = 8x
équation à résoudre : 80 = 8 x ( on divise par 8 les deux membres)
on obtient x
= 10
la largeur du rectangle est de 10 m ; la longueur du
rectangle est de 3 fois 10 m soit 30 m.
vérification : P rectangle = 2 ( L + l )
= 2 ( 30 + 10 ) = 2 ( 40) = 80
N°4 :
Trouver 3 nombres entiers pairs consécutifs dont la somme est égale à 36 . Donner la valeur du premier nombre.
on choisi "x" le premier nombre .
les deux autres nombres sont "x + 2" et " (x+2) + 2 = x +4"
l'énoncer se traduit par l'équation : x + (x+2)
+ (x +4) = 36
soit x + x +x
+2 + 4 = 36 ; 3x + 6 = 36
résolution de
l'équation :
3x + 6 = 36 ; ( on ajoute -6 aux deux membres)
3x + 6 - 6 = 36
- 6 ;
3x = 30 (
on divise les deux membres par 3)
x = 10
conclusion : le premier nombre pair est "
10"
le deuxième nombre est 10 + 2 soit 12 ; le troisième nombre est 12 + 2 = 14
vérification :
10 + 12 + 14 est bien égal à 36 ; donc les trois nombres entiers pairs
consécutifs sont 10 ; 12 ; 14 .
N°5 :
Une ouvrier met 15 minutes pour usiner
une pièce , pour aménager et préparer le poste
de travail il faut prévoir 3h 45 mn. Combien de pièces peut-il usiner sur une semaine de 35 heures ?
Prendre
"x" le nombre de pièces..( transformer la durée en nombre décimal)
l'inconnue est le nombre de pièces usinées.
On met le temps sous forme décimale : 15 mn = 0, 25 h : 3h 45 = 3,
75 h; 35 h ne change pas = 35 h
Mise en équation : 0,25 x +
3,75 = 35
résolution de l'équation :
0,25 x + 3,75 = 35
0,25 x = 35 - 3,75
( un terme change de membre il change de signe )
0,25 x = 31,25 ( on divise 31,25 par 0,25 )
x =![]()
x = 125
le nombre de pièces usiner en une semaine sera de
125 pièces .
N°6 :
trouver trois nombres entiers consécutifs dont la somme est 1884
.( prendre pour inconnue , le plus petit nombre.)
N°7 :
Trouver 3 nombres
multiples de 3 consécutifs dont
la somme est 27
Prendre
pour inconnue le plus petit nombre .
6
+ 9 + 12
N°8 :
Trouver 5 nombres entiers impairs consécutifs dont la somme est 75.
Info :
prendre pour inconnue le nombre médian ( celui qui se trouve au milieu )
Résultat : 11 ; 13 ; 15 ; 17 ;
19
N°9 :Trouver 13 nombres consécutifs dont la somme est 2457 .
Recherche
du 7ème nombre
|
1er nombre |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
x-6 |
x-5 |
x-4 |
x-3 |
x-2 |
x-1 |
x |
X+1 |
X+2 |
X+3 |
X+4 |
X+5 |
X+6 |
On
additionne : il reste « 13 x »
Info
: prendre pour inconnue le nombre médian
( celui qui se trouve au milieu ) donc
le 7ème nombre est 2457 / 13 = 189
|
1er nombre |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
x-6 |
x-5 |
x-4 |
x-3 |
x-2 |
x-1 |
x |
X+1 |
X+2 |
X+3 |
X+4 |
X+5 |
X+6 |
|
183 |
184 |
185 |
186 |
187 |
188 |
189 |
190 |
191 |
192 |
193 |
194 |
195 |
N°10 Quel nombre faut-il multiplier 34 pour
obtenir 25 ? 34 x = 25 ; donc
x = 25 / 34
SUITE Interdisciplinarité :
N°1 Le réservoir d'une voiture est au deux cinquièmes rempli . Il faut
ajouter 38 litres de carburant pour le
remplir entièrement . Quelle est la contenance de ce
réservoir ?
Soit
« x » : la contenance du réservoir
(2/5 ) x + 38 = x ;
![]() x + 38 = x ; 2x +
190 = 5x ; 3x = 190 ; x = 63,33
x + 38 = x ; 2x +
190 = 5x ; 3x = 190 ; x = 63,33
la contenance du réservoir est de 63,33 l
N°2 Le réservoir
d'un voiture est vide aux deux tiers . On
ajoute 30 litres de carburant pour le remplir aux trois quarts .
Quelle est la contenance du réservoir ?
Soit
« x » : la contenance du réservoir.
Il
est au ![]() x plein
x plein
![]() x + 30 =
x + 30 =
![]() x
; 30 =
x
; 30 = ![]() x
-
x
- ![]() x ;
30 = x (
x ;
30 = x (![]() -
- ![]() ) ; 30 = x (
) ; 30 = x (![]() -
- ![]() ) ;
) ;
30
= ![]() x ; x
= ( 30 fois 12 ) / 5 ; x
= 72
x ; x
= ( 30 fois 12 ) / 5 ; x
= 72
la contenance du réservoir est de 72 l
N°3 la
largeur d'un rectangle est le tiers de
sa longueur et le périmètre mesure 48 m . Calculer les
dimensions de ce rectangle . ( 6 et 18 m)
N°4 La
longueur d'un rectangle surpasse de 10
m sa largeur . Le périmètre est de 120 m .Calculer les
dimensions de ce rectangle . ( 25 et 35 m)
N°5 Le 1er
janvier 1997 la population de la
France a été estimée à 58 494 000
habitants se répartissent en 30 017 000 femmes et 28 477 000 hommes.
Quel
pourcentage de la population les femmes et les hommes représentent
- ils ?
Soit
x1 le % de femmes et x2 le % d ’ hommes .
x1 = ( 30 017 000 / 58 494 000 ) fois 100 = 0,513 fois 100 = 51,3
et
x2 = ( 28
477 000/ 58 494 000 ) fois 100 = 0,487
fois 100 = 48,7
le % de femmes est
de 51,3% et le % d ’ hommes 48,7 %
N°6 Augmenter un nombre de x %
, c'est multiplier ce nombre par
( 1 + ![]() )
ou ( 1 + 0,01x )
)
ou ( 1 + 0,01x )
Pour
calculer le pourcentage d'augmentation du prix d'un objet qui passe
de 34 à 39,5 € ,
on écrit : 39,5 = 34 ( 1 + 0,01 x)
Ecrire
cette équation sous la forme ax + b = c , puis la résoudre
( arrondir à 0,01 près , ou à 2
décimales).
0,34
x + 34 = 39,5 ; 0,34 x = 39,5 - 34 ; 0,34 x = 5,5
; x = 5,5 / 0,34 ; x = 16,18
Enoncer le
résultat sous forme d'une phrase .
Le
pourcentage d’augmentation est de 16,18
%
N°7
Calculer le pourcentage d'augmentation de la population d'un village qui passe
de 3764 habitants à 3978 .
on écrit : 3978 = 3764 ( 1 + 0,01 x) ; 3978 = 3764 + 37,64
x ;
3978
- 3764
= 37,64 x ;
x = 5,69
Le
pourcentage d’augmentation est de
5,69 %
N°8 un centre de formation organise un voyage
.Le transporteur propose un prix global correspondant à 160 €
par personne . Si le nombre de personnes
augmente de 5 , on passe pour le même prix global , à 120 € par personne.
Combien de
personnes participent au voyage ?
y = 160 x
ou y = 120 ( x + 5 ) ; 160 x = 120 x + 600
140 x =
600 ; x = 600/ 140 ; x = 4,29
Le
pourcentage d’augmentation est de 4,29 %
N° 9 La durée de fabrication d'une pièce est de
6,50 mn.
Au cours
d'une journée de 8 h , combien peut-on fabriquer de
pièces sachant qu'il faut compter 1 h 30 mn pour le réglage la machine et
l'affûtage de l'outil et l'approvisionnement .
8
fois 60 = 6,5 x
+ 90 ; 480 = 6,5 x
+ 90 ; 390 = 6, 5
x ; x = 60
N° 10
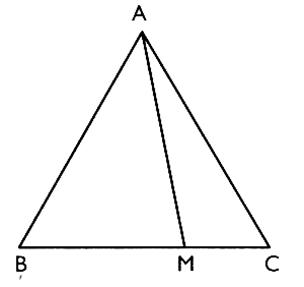
|
ABC est
un triangle équilatéral de côté 6 cm
.On place sur le côté [BC] le point M
tel que BM = d. 1°)
calculer la hauteur du triangle ABC , puis l'aire du
triangle . réponse : AM = 2) où doit -on placer le point M pour que l'aire du triangle AMC
soit égal à 10 ? |
|
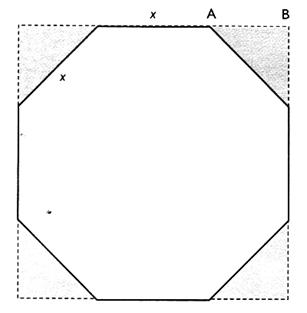
N°11 .
|
On veut
découper dans une plaque carrée de 0 cm de côté un octogone régulier de côté
"x". a)
Sachant que chaque triangle hachuré est un triangle
rectangle isocèle , déterminé la mesure de chacun de
leurs angles aigus « a ». 180° = 90° + 2 « angle a » ; donc l’angle
« a » est de 45° b)
Calculer la longueur
AB en fonction de "x" , puis la
longueur "x". AB est la longueur du côté d’un carré ,
« x » est la diagonale du carré. x²
= 2 AB² AB² = x² / 2 donc AB = x / Longueur
de « x » : 100 = 2 fois 1,414 x + x 100 = 2,828 x + x = 3,828 x x = 100 : 3,828 |
|
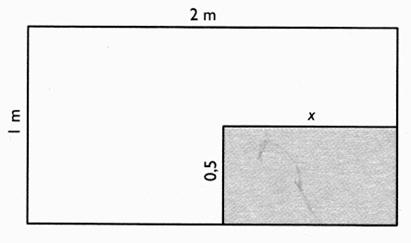
N°12
|
Dans une pièce
rectangulaire de 2 m de longueur et de 1 m de large ,
on effectue une découpe de forme rectangulaire comme l'indique la figure ci
-dessous. Donner
l'expression de l'aire de la partie restante en fonction de "x". Calculer
"x" pour que l'aire de la partie restante soit 1,25 m² . |
|
|
Aire
de la pièce : 2 m ² ;
2
m² - 1,25 m² = 0,5x
0,75
m² = 0,5 x ; x = 1,5
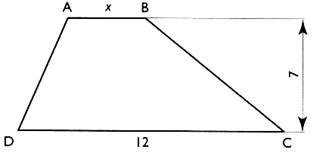
N°13
|
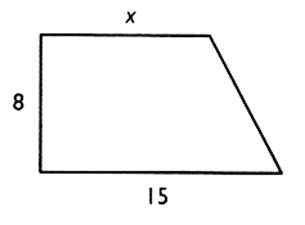
On
considère un trapèze ABCD. Vérifier
que l'aire du trapèze peut s'écrire : A = 8,5 x Calculer
" x " pour que l'aire du trapèze soit égale à 172,2 cm² ( arrondie à deux décimales) |
|
A
= [( 12+ x ) 7 ] / 2 = ( 84
+ 7x) / 2 = 42 + 3,5 x
172,2 =
42 + 3,5 x
172,2
- 42 =
3,5 x
130,2 =
3,5 x ; x = 37,2
la valeur 37,2 ne vérifie pas l’égalité . A = 8,5 x
N° 14
|
Un
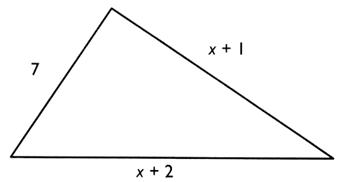
triangle a les dimensions ( en m) indiquées sur la
figure . Exprimer
le périmètre du triangle en fonction de "x". Calculer
"x" pour que le périmètre
soit égal à 30 m . En déduire les dimensions
du triangle . |
|
Périmètre = 7 + x + 1
+ x + 2
30
= 7 + x + 1 + x + 2
30
= 10 + 2x
20
= 2x
10
= x
les dimensions des triangle sont
7 ; 10 +1 ( = 11) ; 10+2 ( = 12)
N°15
|
Montrer
que l'expression de l'aire du trapèze
rectangle en fonction de "x" est : A = 4 x + 60 Calculer
"x" pour que l'aire du trapèze rectangle soit égale à 200 cm² . Pour cela , résoudre
l'équation : 4x + 60 = 200 |
|
A
= ( x + 15 ) 8
/ 2 = ( 8x + 120 ) /2 = 4x + 60
200
= 4x + 60 ; 140 = 4x ; x =
35