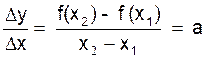|
OBJECTIFS : - Savoir |
I ) Pré requis:
|
|
|
|
|
i9
|
:i |
|
|
i9
|
:i |
II ) ENVIRONNEMENT du dossier :
|
Dossier précédent : |
Dossier suivant : |
Info : |
III ) LECON : FONCTION AFFINE ET
APPLICATIONS (niveau
seconde prof)
IV)
INFORMATIONS « formation
leçon » :
|
Travaux auto - formation. |
|
Corrigé des travaux auto - formation. |
||||
|
Travaux interdisciplinaires : |
Corrigé |
|||||
|
|
|
|
|
|
|
|
V ) DEVOIRS ( écrits):
|
Devoir diagnostique L tests. |
|
|
Devoir Auto
- formatif
(intégré au cours) |
|
|
Devoir
Formatif « Contrôle :
savoir » ; (remédiation) |
|
|
|
|
|
Devoir sommatif. |
|
|
Devoir certificatif : (remédiation) |
|
* remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour conclure une formation .
|
Titre |
|
|
N° |
CHAPITRES :
Rappels sur la fonction affine :
A) définition :
B)
Représentation graphique.
C)
taux de variation.
Détermination de l’équation d’une droite.
|
Rappels sur la fonction affine |
%º@ |
A)
définition :
Les nombres « a » et
« b » étant donnés, on appelle « fonction affine » la
fonction « f » qui au nombre réel « ![]() »
fait correspondre le nombre «
»
fait correspondre le nombre « ![]() »
»
On a :
f (![]()
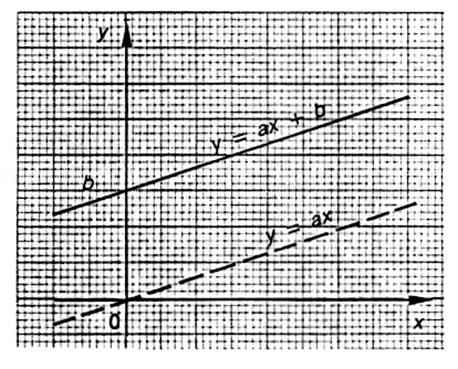
B) Représentation graphique.
La représentation graphique de la
fonction affine ![]() est une droite.
est une droite.
Le nombre « ![]() »
est le
coefficient directeur ( « a » est égale à la tangente de l ‘angle que fait la droite
et l’axe des abscisses)
»
est le
coefficient directeur ( « a » est égale à la tangente de l ‘angle que fait la droite
et l’axe des abscisses)
Le nombre « ![]() »
est l’ordonnée à l’origine .
»
est l’ordonnée à l’origine . ![]()
|
La droite « |
|
C) taux de variation.
Considérons la fonction affine ![]() .
.
Nous calculons le taux de variation
entre x1 et x2 ( avec x1 "` x2 ) :
![]() 1
1 ![]() 2
2![]() ( ax2 + b
) - ( a x1 +b )
( ax2 + b
) - ( a x1 +b )
= ax2 + b -
a x1 - b
= ax2 -
a x1
f (x1
) -
f (x2 ) = a ( x2 - x1
)
|
On note : et
on écrira :
|
|
Nous constatons que :
Quels que soient x2
- x1
, le taux de variation de la fonction affine ![]() est constant et égal à « a ».
est constant et égal à « a ».
On en déduit que : si « a » > 0 la fonction affine est constante.
si « a »
< 0 la fonction affine est décroissante.
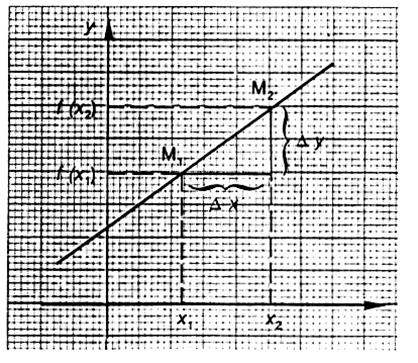
Activité 1:
Représenter graphiquement la fonction f :
x -2 x + 5
|
La fonction « f » est
affine. Sa représentation graphique est une
droite. Pour tracer cette droite il suffit
de prendre 2 points. Si « x » = 0 , y = 5 : la droite passe par le point A (
0 ;5 ) Si x = 3 ,
y = -1 : la droite passe par le point B ( 3 ; -1) La représentation graphique de la
fonction « f » est la droite (AB) |
|
Exemple d’ application:
Recherche du seuil de rentabilité
d’une agence de voyages.
Cette agence négocie avec une
compagnie aérienne le prix des billets
d’avion pour un voyage qu’elle compte organiser.
Deux tarifications sont proposés par la compagnie aérienne:
1ère solution : Par
vol normal, le prix du billet du voyage est proposé 400 € par voyageur, quelque soit le
nombre de passagers.
2ème solution : Un
avion est affrété spécialement, dans ce
cas l’agence de voyage doit verser à la compagnie une somme fixe de 24 000
€ et le tarif forfaitaire d’un billet
« voyageur » sera de 250 € .
On désire déterminer à partir de quel
seuil de passagers il devient rentable
d’affréter un avion pour ce voyage. ?
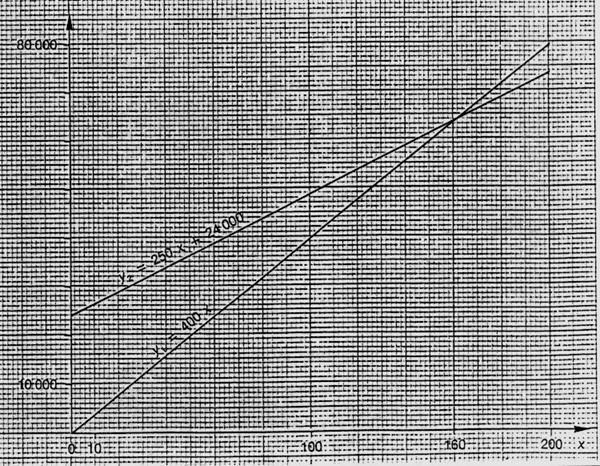
Etude graphique :
La fonction « x » ; y1
= 400 x est une fonction linéaire.
La fonction « x » : y2
= 250 x + 24 000 est une fonction
affine.
|
Nous représentons ces deux fonctions
dans un même repère. |
|
Nous voyons que :
-
Pour
x < 160 voyageurs ; y 1
< y2 , pour l’agence , la solution
du billet à 400 € est préférable.
-
Pour x =
160 voyageurs ; y 1 =
y2 ,
les deux solutions se valent.
-
Pour x > 160 voyageurs ; y 1
> y2 , l’ agence a intérêt à affréter un avion.
Par le calcul :
Une autre façon de trouver le nombre de passagers était de résoudre le système constitué
par les deux équations :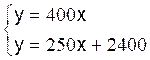
|
%Ä@Déjà vu 1 |
Détermination de l’équation d’une droite. |
%º@ |
|
Leçon |
Titre |
|
N° |
TRAVAUX
d ’ AUTO – FORMATIFS
sur FONCTION
AFFINE ET APPLICATIONS Refaire
les exercices du cours . |
TRAVAUX N° d
’ AUTO - FORMATION : CONTROLE
TRAVAUX N° d ‘ AUTO - FORMATION EVALUATION