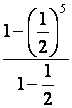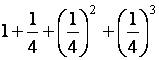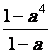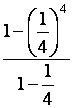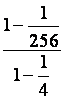Pré requis :

les ensembles de nombres

Index : warmaths

1°)Liste des objectifs en calcul numérique

Complément d’informations :

2°) liste « algèbre »

Rappels de cours. Les ensembles Réels

ICI TESTS sur l’ensemble du calcul algébrique .

Consigne :

1.      info ++

Calculer l’expression suivante :    ( a + b ) ( a² - ab + b ²)

La multiplication étant distributive par rapport à l’addition on a :

( a + b ) ( a² - ab + b²)=  a ( a² - ab + b²) +  b ( a² - ab + b²)

ainsi :

( a + b ) ( a² + ab + b²) = a ³ -  a ² b + a b ² + b a² - ab² + b³

^{après simplification on en déduit :}

( a + b ) ( a² + ab + b²) = a ³ + b³

2.       

Calculer l’expression suivante :    ( a -  b ) ( a² + ab + b²)

La multiplication étant distributive par rapport à l’addition on a :

( a -  b ) ( a² +  ab + b²)=  a ( a² +  ab + b²) -  b ( a² +  ab + b²)

ainsi :

( a - b ) ( a² + ab + b ² ) = a ³ +   a ² b + a b ² - b a² - ab² + b³

^{après simplification on en déduit :}

(a - b ) ( a² + ab + b²) = a ³ -  b³

3.       

Calculer l’expression suivante :    ( a -1  ) ( a³ + a ²  + a + 1 )

En développant le produit :

( a -1  ) ( a³ + a ²  + a + 1 ) =  a ⁴ + a ³ + a² + a – a ³ – a ² - a – 1

Donc en simplifiant , cela devient :  ( a -1  ) ( a³ + a ²  + a + 1 ) =  a ⁴ – 1

4.       

Calculer l’expression suivante :    ( a -b  ) ( a³ + a ²b   + a b²  - b ³ )

En développant le produit :

( a -b ) ( a³ + a ² b   + a b²  - b ³ ) = a ⁴ – a ³ b + a² b ² - a b³ – b a ³ + a² b ² - a b ³ + b ⁴

Ce qui donne en ordonnant les puissances par ordre décroissantes  de « a » 

( a -b ) ( a³ + a ² b   + a b²  - b ³ ) = a ⁴ – 2 a ³ b + 2 a² b ² - 2 a b³ + b ⁴ 

5.       

Calculer l’expression suivante :    ( a + b + c  ) ( a ²  +b ² + c²  - ab – ac – bc)

On désigne par  « X »  le produit ( a + b + c  ) ( a ²  +b ² + c²  - ab – ac – bc ) 

X  =  a ³  + a b² + a c² - a² b – a² c – a b c + b a² + b ³ + b c ² - ab² - a b c  - b² c + a² c + b² c + c ³ – a b c – a c² - b c²  .

En simplifiant , il devient :

( a + b + c  ) ( a ²  +b ² + c²  - ab – ac – bc )  =  a ³ + b ³ + c ³ – 3 a b c .

6.       

Calculer l’expression suivante :  

a (  b + c - a ) ²  + b ( c + a – b ) ² + c ( a + b – c ) ²  + ( b + c  - a ) ( c + a – b ) ( a + b – c )

Tout d’abord calculons d’une manière générale l’expression ( x + y - z ) ² :  ( voir forme développer  ( A – B)² ) 

( x + y - z ) ² =  ( ( x+y ) – z ) ² =  ( x + y ) ² + z ² - 2 ( x + y) z.

donc :  ( x + y - z ) ² = x ² + y² + 2 x y + z² - 2 x z – 2 y z .

en ordonnant on obtient : ( x + y - z ) ² = x ² + y² + z ² +  2 x y  - 2 x z – 2 y z .

Alors en appelant « X » la somme a (  b + c - a ) ²  + b ( c + a – b ) ² + c ( a + b – c ) ²

On a

X = a ( b² + c² + a² + 2 bc – 2 ac – 2 ab ) + b ( c² + a² + b² + 2 ac – 2 bc – 2 ab) + c ( a² + b² + c² + 2 ab – 2 ac – 2 bc )

Donc :

X  = a b² +  ac² + a ³ + 2 a b c – 2 a² c – 2 a² b + bc ² + a² b + b³ + 2 abc  - 2 b² c – 2 a b² + a² c + b² c + c ³ + 2  a bc  - 2 a c² - 2 b c²

Ou

X =  a ³ + b ³ + c ³ – a² b – a b² - a² c – a c² - b² c – b c² + 6 abc.

Calculons maintenant le produit « Y » , avec :

Y = ( b + c – a ) ( c + a – b) ( a + b – c)

Y = ( b + c – a ) ( ac + bc – c² + a² + ab – ac – ab – b²  + bc )

Y = ( b + c – a ) ( 2 bc + a² - b² - c² )

Y = 2 b² c + a² b – b³ – bc ² + a² c – b²c – c ³ – 2 abc – a ³ + a b² + ac²

Y =  - a ³ – b ³  - c ³ + a² b + ab² + a² c + a c² + b² c – 2 abc

Donc : X + Y = 4 abc

D’où :

a (  b + c - a ) ²  + b ( c + a – b ) ² + c ( a + b – c ) ²  + ( b + c  - a ) ( c + a – b ) ( a + b – c ) = 4 abc

7.       

Calculer l’expression suivante :

Y =  a ²(  b + c - a )  + b² ( c + a – b )  + c ² ( a + b – c )   - ( b + c  - a ) ( c + a – b ) ( a + b – c )

Y =  a ²(  b + c - a )  + b² ( c + a – b )  + c ² ( a + b – c )   - ( b + c  - a ) ( c + a – b ) ( a + b – c )

Y =  a² b + a²c – a ³ + b² c + a b² - b ³ + a c² + b c² - c ³

Donc :Y =  - a ³ – b ³ – c ³ + a² b + a² c + a c² + b² c + b c²

Soit  X  = ( b + c  - a ) ( c + a – b ) ( a + b – c )

X  =  ( b + c  - a ) (  ac + bc  - c² + a² + ab – ac – ab – b² + bc )

X  =  ( b + c  - a ) ( 2 bc + a² - b² - c² )

X = 2 b²c + a² b – b³ – bc² + 2 bc² + a² c – b²c – c ³ – 2 abc – a ³ + a b² + a c²

X = - a ³ – b ³ – c³ + a² b + ab² + a²c + ac² + b²c + b c² - 2 abc.

Donc Y – X = 2 abc , d’où

a ²(  b + c - a )  + b² ( c + a – b )  + c ² ( a + b – c )   - ( b + c  - a ) ( c + a – b ) ( a + b – c )= 2 a b c

8.       

Calculer l’expression suivante :

( a + b + c) [ ( a – b ) ²   + ( b – c ) ²  + ( c – a ) ² ]

Nous savons que  ( x – y ) ² = x² - 2 x y + y ² , on en déduit alors en appelant « X » l’expression à calculer

X = ( a + b + c) ( a² + b² - 2 ab + b² + c² - 2 bc + c² + a² - 2 ac )

X =  ( a + b + c) ( 2 a² + 2 b² - 2 ab + 2 c² - 2 bc - 2 ac )   ( on factorise avec 2)

X =  ( a + b + c) (  a² +  b² +  c² -  ab -  bc -  ac )

En développant ce dernier produit , on obtient :

X = a ³ + a b² + a c² - a²b – abc – a²c + a²b + b³ + bc² - a b² - b²c 6 abc + a²c + b²c + c ³ – a bc – b c² - a c²

D’où , après simplification , il vient :

( a + b + c) [ ( a – b ) ²   + ( b – c ) ²  + ( c – a ) ² ] =  a ³ + b³  + c³ – 3 abc

9.       

Vérifier l’identité suivante : :

    a² ( b – c ) + b² ( c – a) + c²  ( a – b) =  ( c- b ) ( b – a ) ( a – c )

Développement du deuxième membre :

( c- b ) ( b – a ) ( a – c ) =  ( c b – ca – b² + ab ) ( a – c )

( c- b ) ( b – a ) ( a – c ) = cba – a² c – a b² + a²b – b c² + a c² + b² c – abc .

donc :  ( c- b ) ( b – a ) ( a – c ) =  - a ²c + a² b – b² a + b² c – c² b + c² a

d’où : ( c- b ) ( b – a ) ( a – c ) = a² ( b –c ) + b² ( c –a ) + c² ( a –b)

soit enfin :

                    a² ( b – c ) + b² ( c – a) + c²  ( a – b) =  ( c- b ) ( b – a ) ( a – c )

10.  

Vérifier l’identité suivante : :

    a  ³ ( b – c ) + b³  ( c – a) + c³   ( a – b) =  ( a + b + c ) ( c- b ) ( b – a ) ( a – c )

( c- b ) ( b – a ) ( a – c ) =  ( cb – ca – b² + ab) ( a – c )

( c- b ) ( b – a ) ( a – c ) =  cba – a² c – a b² + a² b – b c² +  a c² + b² c – a bc

( c- b ) ( b – a ) ( a – c ) = - a² c + a² b – b²a + b² - c² b + c² a

donc : ( a + b + c ) ( c- b ) ( b – a ) ( a – c ) =  ( a + b + c ) (- a² c + a² b – b²a + b² - c² b + c² a )

Soit X cette expression , alors :

X =  - a ³ c + a³ b – b² a² + b² ac – a c²b + a² c² - a² bc + a²  b² - b ³ a + b ³ c – b² c² + a b c² - a² c² + a² bc – a b² c + b² c² - b c ³ + a c ³

On obtient en simplifiant :

 X  = - a ³ c + a ³ b – b ³ a +  b ³ c – c ³ b +  c ³ a

X = a ³ ( - c + b ) +  b ³  ( c – a ) + c³ ( - b + a )

D’où :

      a  ³ ( b – c ) + b³  ( c – a) + c³   ( a – b) =  ( a + b + c ) ( c- b ) ( b – a ) ( a – c )

11.  

Vérifier l’identité suivante :

( a + b + c)²  +  ( b + c – a ) + ( c +  a - b )² + ( a + b - c)² = 4 ( a ² + b² + c² )

Tout d’abord calculons d’une manière générale l’expression ( x + y - z ) ² :  ( voir forme développer  ( A + B)² ) 

( x + y + z ) ² =  ( ( x+y ) + z ) ² =  ( x + y ) ²  + 2 ( x + y) z. + z ²

donc :  ( x + y + z ) ² = x ² + y² + 2 x y + z² + 2 x z +  2 y z .

en ordonnant on obtient : ( x + y + z ) ² = x ² + y² + z ² +  2 x y  +  2 x z +  2 y z .

et l’on a aussi : donc   :     ( x + y - z ) ² = x ² + y² + z ² +  2 x y  - 2 x z – 2 y z .

avec cela , on a alors :

·        ( a + b + c ) ² =  a² + b² + c² + 2ab + 2ac + 2 bc

·        (  b + c – a  ) ² =  a² + b² + c² -  2ab -  2ac + 2 bc

·        ( c + a – b  ) ² =  a² + b² + c² -  2ab + 2ac - 2 bc

·        ( a + b - c ) ² =  a² + b² + c² + 2ab -  2ac -  2 bc

En additionnant  membre à membre ces quatre égalités on obtient alors.

( a + b + c ) ² + (  b + c – a  ) ² + ( c + a – b  ) ² + ( a + b - c ) ² =  4  ( a ² + b² + c² )

12.  

Vérifier l’identité suivante :

(  a + b ) ³ -  ( a ³ +  b ³ ) =  3 a b ( a + b )

On a (  a + b ) ³ =  ( a + b )² ( a + b) =  ( a² + 2 ab + b² ) (  a + b )

Donc : (  a + b ) ³ = a ³ + a² b + 2 a² b + 2 a b² + a b² + b ³ 

Soit :   (  a + b ) ³ = a ³ +3  a² b + 3 a b²  + b ³ 

Cette formule se retrouve également grâce au triangle de Pascal)

On a alors :

(  a + b ) ³ -  ( a ³ +  b ³ ) =   a ³ +3  a² b + 3 a b²  + b ³   -  a ³  - b ³

en simplifiant il vient donc : (  a + b ) ³ -  ( a ³ +  b ³ ) =  3  a² b + 3 a b²

et en mettant «  3 ab » en facteur on obtient :

(  a + b ) ³ -  ( a ³ +  b ³ ) =  3 a b ( a + b )

13.  

Vérifier l’identité suivante :

(  a -  b ) ³ -  ( a ³ -   b ³ ) =  3 a b ( a -  b )

On a (  a -  b ) ³ =  ( a - b )² ( a -  b) =  ( a² - 2 ab + b² ) (  a - b )

Donc : (  a -  b ) ³ = a ³ - a² b -  2 a² b + 2 a b² + a b² -  b ³ 

Soit :   (  a -  b ) ³ = a ³ - 3  a² b + 3 a b²  -  b ³ 

en simplifiant il vient donc : (  a -  b ) ³ -  ( a ³ -  b ³ ) =  - 3  a² b + 3 a b²

et en mettant «  3 ab » en facteur on obtient :

(  a -  b ) ³ -  ( a ³ -   b ³ ) =  3 a b ( a -  b )

14.  

Vérifier l’identité suivante :

(  a + b + c  ) ³ -  ( a ³ +  b ³ + c ³ ) =  3 ( a + b ) ( b + c ) ( c + a )

On écrit :

(  a + b + c  ) ³ = (  a + b + c  )² (  a + b + c  )

(  a + b + c  )² =  (  a + ( b + c )  )² = a² + 2 a ( b + c )+  ( b + c )²

donc : (  a + b + c  )² = a² + 2 ab + 2 ac + b² + c² + 2 bc.

Alors : (  a + b + c  ) ³ = (  a² + 2 ab + 2 ac + b² + c² + 2 bc.  )² (  a + b + c  )

D’où

(  a + b + c  ) ³ = a ³ + a b² + a c² + 2 a² b + 2 a² c + 2 bca + a² b + b ³ + b c² + 2 ab² + 2 a bc + 2 b² c + a² c + b² c + c³ + 2 a bc + 2 a c² + 2 b c².

donc :

(  a + b + c  ) ³ = a ³ + b ³  + c ³ + 3 a² b + 3  a² c + 3 b² c + 3 b² a + 3 c² a  + 3 c² b + 6 a bc .

soit :

(  a + b + c  ) ³ -  ( a ³ +  b ³ + c ³ ) = 3 a² b + 3  a² c + 3 b² c + 3 b² a + 3 c² a  + 3 c² b + 6 a bc .

on a alors :

(  a + b + c  ) ³ -  ( a ³ +  b ³ + c ³ ) = 3 ( a² b +  a² c +  b² c +  b² a +  c² a  +  c² b + 2 a bc )

ou encore :

(  a + b + c  ) ³ -  ( a ³ +  b ³ + c ³ ) = 3 [( a ( a b +  a c +   c² +  bc  )  +  b ( b c +  ba + c²  +2 ac )]

(  a + b + c  ) ³ -  ( a ³ +  b ³ + c ³ ) = 3 [( a ( a ( b + c)  +  c (  c +  b  )  +  b ( b ( c +  a)  + c( c + a  )]

donc :

(  a + b + c  ) ³ -  ( a ³ +  b ³ + c ³ ) = 3 [( a (  ( b + c)  (  a +  c  ))   +  b ( ( c +  a) ( b + c ))]

et enfin

(  a + b + c  ) ³ -  ( a ³ +  b ³ + c ³ ) =  3 ( a + b ) ( b + c ) ( c + a )

Nota : la méthode qui consiste à développer l’un après l’autre les deux membres de l’identité , puis à constater l’égalité par comparaison est aussi valable.

15.  

Calculer le produit :

 ( 1 – a ) (  1 + a + a ² + a ³ + a ⁴ ).

En déduire  le nombre :

( 1 – a ) (  1 + a + a ² + a ³ + a ⁴ )= 1 + a + a ² + a ³ + a ⁴   - a – a² - a³  - a ⁴ – a ⁵ =  1 – a ⁵

Soit X le nombre :  ;

X =

Or d’après ce qui précède :

  ( )    =  1  -

  (  X   )    =  1  -

X  =  =   = = =  = 

Autre solution : mettre tout sous la forme de fractions de même dénominateur..

16.  

Calculer le produit :

En s’inspirant de l’exercice précédent, calculer le plus simplement possible.

E ₁ =     et   E ₂ = 

E ₁ =        =   comme  nous l’avons vu dans l’exercice précédent :

 =  = =  =   = 

E ₁ =    =

E ₂ = 

E =

Calculons : ( 1 – a ) (  1 + a + a ² + a ³ )

 ( 1 – a ) (  1 + a + a ² + a ³ ) =   1 + a + a ² + a ³ + a ⁴   - a – a² - a³  - a ⁴  =  1 – - a ⁴

donc si « a » est différent de « a » : 1 + a + a ² + a ³  =

Voir l’exercice N°15 ….

Alors : =  =    =   =   =

=

Autre solution : mettre tout sous la forme de fractions de même dénominateur..

17.  

Vérifier l’identité suivante (  dit aussi : identité de Lagrange)

( a ² + b² ) ( a ‘ ² + b’ ²) = ( a a ‘  + b b ‘ ) + ( a b ‘  - b a ‘ ) ²

Il y a deux méthodes possibles :

1°) méthode :Développer les deux membres de l’identité séparément et vérifier leur égalité.

2°) méthode : ( a² + b² ) ( a ‘ ² + b ‘ ² )= a² a ‘ ² + a² b ‘ ² + b ² a ‘ ² + b ² b ‘ ²

ajoutons le terme nul : 2 a a’  b b’  -  2 a a ‘ b b ‘ , on a donc :

( a² + b² ) ( a ‘ ² + b ‘ ² )= a² a ‘ ² + a² b ‘ ² + b ² a ‘ ² + b ² b ‘ ² + 2 a a’  b b’  -  2 a a ‘ b b ‘

( a² + b² ) ( a ‘ ² + b ‘ ² )= ( a a ‘ )  ²  + 2 (a a’) ( b b’)  + ( b  b ‘ ) ² -  2 ( a a ‘ ) ( b b ‘ ) + (a b ‘ ) ² + ( b  a ‘ )²

soit                ( a² + b² ) ( a ‘ ² + b ‘ ² )=  ( a a ‘ + b b’ ) ²  + ( a b ‘  - b a ‘ ) ²

l’identité de Lagrange est donc bien vérifiée…

18.  

Vérifier l’identité suivante (  dit aussi : identité de Lagrange)

( a ² + b² + c ²) ( a ‘ ² + b’ ²  +  c’ ² ) =  ( a a ‘  + b b ‘ + c c’ ) + ( a b ‘  - b a ‘ ) ² + ( a c’ – c a ‘ )² + ( b c’ – c b ‘ ) ²

( a ² + b² + c ²) ( a ‘ ² + b’ ²  +  c’ ² ) = a² a ‘ ² + a² b ‘ ² + a² c’ ² + b² a’ ² + b ² b’ ² + b² c’ ² + c² a ‘ ² + c ² b ‘ ² + c ² c’ ²

ajoutons le terme nul .

2 a a ‘ b b’ – 2 a a ‘ b b’ + 2 a a ‘ c c’ – 2 a a ‘ c c’ + 2 b b ‘ c c’ – b b ‘ c c’ .

alors

( a ² + b² + c ²) ( a ‘ ² + b’ ²  +  c’ ² ) = ( a² a ‘ ² + b ² b ‘ ² + c ² c’ ² + 2 a a ‘ b b’ + 2 a a ‘ c c’+ 2 b b ‘ c c’) + ( a ² c’ ² - 2 a c’ c a ‘ +a ‘ ² c ² ) + ( b ² c’ ² - 2 b c’ b ‘ c + b ‘ + c ²)

or

 a² a ‘ ² + b ² b ‘ ² + c ² c’ ² + 2 a a ‘ b b’ + 2 a a ‘ c c’+ 2 b b ‘ c c’ = ( a a ‘ + b b ‘ + c c’ ) ²

donc :

( a ² + b² + c ²) ( a ‘ ² + b’ ²  +  c’ ² ) =  ( a a ‘  + b b ‘ + c c’ ) + ( a b ‘  - b a ‘ ) ² + ( a c’ – c a ‘ )² + ( b c’ – c b ‘ ) ²

Nota : On peut également développer chaque membre et en déduire l’égalité …

19.  

Vérifier l’identité d’ Euler.

( a ² +  b² + c² + d² ) ( a ‘ ² + b ‘ ² + c ’ ²  +  d ’ ² ) =  ( a a ‘  + b b ‘ + c c’ + d d ’ )² + (  a’ b – a b ‘ + d c’ – c d’ ) ² + ( c a ‘ – d b ‘ – a c’ + b  d’ ) ² + ( d a ‘ + c b ‘ – b c’ – a d’ ) ²

Elle prouve que si deux entiers sont chacun la somme de quatre carrés , leur produit a la même propriété )

On a :

( a ² +  b² + c² + d² ) ( a ‘ ² + b ‘ ² + c ’ ²  +  d ’ ² ) =  A

         A    =     a² a ‘ ² + a ² b ‘ ² + a² c’ ² + a ² d’ ² + b ² a ‘ ² + b ² b ‘ ² + b ² c’ ² + b ² d ’ ²  + c ² a ‘ ² + c ²  b ‘ ² + cx c’ ² + c ² d’ ² + d ² a ‘ ² + d ² b ‘ ² + d ² c’ ² + d ² d’ ²

Comme dans les deux exercices précédents ajoutons le terme nul :

2 a a ‘ b b’ +  2 a a ‘ c c ’ + 2 a a ‘ d d ’ +  2 bb ‘ c c’ + 2 b b ‘ dd ’ – 2 dd ‘ c c’ . – b a’ a b ‘ – 2 c a ‘ a c’ – 2 d a ‘ a d’ – 2 c b ‘ b c’  - 2 b d’ d b ‘ – 2 d c’ c d ’ + 2 b a ‘ d c’ – 2 b a ‘ c d’ – 2 a b ‘ d c’ + 2 a b ‘ c d’  + 2 c a ‘ b d’ – 2 c a ‘  d b ‘ + 2 d b ‘ a c’ – 2 a  c’ b d’ 2 d a ‘ c b ‘ – 2 d a ‘ b c’ – 2 c b  ‘ a d’ + 2 b c’ a d’

en regroupant les termes de façon convenable , on obtient :

( a ² + b ² + c ² + d ² ) ( a ‘ ² + b ‘ ² + c’ ² + d’ ² ) = X

avec :

X = ( a ² a ‘ ² + b ² b ‘ ² + c ² c’ ² + d ² d’  ² + 2 a a’ b b’ + 2 aa’ dd’ + 2 aa’cc’ + 2 bb’ cc’ + 2 bb’ dd’ + 2 cc’ dd’ ) + ( b² a’² + a² b’² + c² d’² + d² c’² - 2 ba’ab’+ 2 ba’dc’-2ba’cd’-2ab’dc’+2ab’cd’-2dc’cd’)+ (c²a’²+ d²b’²+ a²c’²+b²d’²- 2 ca’db’-2ca’ac’+2ca’bd’+2db’ac’-2db’bd’-2ac’bd’)+ ( d²a’²+c²b’²+b²c’²+a²d’²+2da’cb’-2da’bc’-2da’ad’-2cb’bc’-2cb’ad’+2bc’ad’)

De plus, on a

( x + y + z + t ) ²  = x² + y² + z²+ t² + 2xy + 2 xz + 2 x t + 2y z + 2 y t + 2 z t

on reconnaît alors  

X = ( aa’ + bb’+ cc’+ dd’)² + ( b a’ – ab’+dc’-cd’)² + ( ca’ – db’ – ac’ + bd’)² + ( da’-ad’+cb’-bc’)²

La formule est donc bien vérifiée.

20.  

Vérifier l’identité d’ Euler.

( a + b + c ) ⁵ -  ( a + b – c ) ⁵  - ( b + c – a ) ⁵  - ( c + a – b )⁵ =  80 a b c ( a² + b² + c² )

Dans un premier temps développons ( x + y ) ⁵ 

( x + y ) ⁵  =  ( x + y ) ³( x + y ) ²  = ( x ³ + 3 x² y + 3x y² + y  ³) ( x² + 2 xy + y² )

( x + y ) ⁵  = x ⁵ + 2 x ⁴ y + x³ y² + 3 x ⁴ y + 6 x ³ y² + 3 x ² y ³  + 3 x ³ y² + 6 x² y ³ + 3 x y ⁴ + y ³ x² + 2 x y ⁴ + y ⁵

donc : ( x + y ) ⁵  = x ⁵ + 5 x ⁴ y + 10 x ³ y² + 10 x² y ³ + 5 x y ⁴  + y ⁵

on a alors :

X = ( a + b + c ) ⁵ – (  a + b + c )⁵ = ( ( a + b ) + c ) ⁵  - (  ( a + b ) – c ) ⁵

X =  ( a + b ) ⁵ + 5  ( a + b ) ⁴ c  + 10 ( a + b ) ³ c² +  10 ( a + b ) ² c ³ + 5 ( a + b ) c ⁴ + c ⁵  - [  ( a + b ) ⁵ -  5  ( a + b ) ⁴ c  + 10 ( a + b ) ³ c² -  10 ( a + b ) ² c ³ + 5 ( a + b ) c ⁴ - c ⁵   ]

Donc en simplifiant : X = 10  ( a + b ) ⁴ c  + 20 ( a + b ) ² c ³ + 2 c ⁵  

De même

Y =  -  ( b + c – a ) ⁵  - ( c + a – b )⁵ =    ( - b -  c  +  a ) ⁵  -  ( c + a – b )⁵

Alors :   Y = (  ( a + b ) - c  ) ⁵  -  (  ( a -  b ) + c  ) ⁵

Donc :

Y =  ( a -  b ) ⁵ -  5 ( a -  b ) ⁴ c + 10 ( a -  b ) ³ c² - 10 ( a +-  b ) ² c ³ + 5 ( a -  b ) c ⁴ -  c ⁵  - [  ( a -  b ) ⁵ +   5  ( a -  b ) ⁴ c  + 10 ( a -  b ) ³ c² + 10 ( a - b ) ² c ³ + 5 ( a -  b ) c ⁴ - c ⁵  ]

Donc , après simplification , il vient :

Y = - 10 ( a – b ) ⁴ c – 20 ( a – b ) ² c ³ – 2 c ⁵

D’où     X + Y =  10 c [  ( a + b ) ⁴ – ( a – b ) ⁴ ] + 20 c ³ [( a + b ) ²  - ( a – b ) ² ]  + 20 c ³  [ ( a + b ) – ( a – b ) ] [ ( a + b ) + ( a – b ) ]

Or : ( a + b ) ² + ( a – b ) ² =  a² + b² +  2ab + a² + b² - 2 ab = 2 ( a² + b ² )

Et     ( a + b ) ² -  ( a – b ) ² =  a² + b² +  2ab – (  a² + b² - 2 ab )  = 4 ab

Donc  X + Y =  10 c ( 4 ab ) 2 ( a² + b² ) + 20 c ³ ( 2 b ) ( 2 a )

On a donc : X + Y = 80 cab ( a² + b² ) + 80 c ³ ab

En mettant « 80 abc » en facteur , on  obtient finalement  X + Y = 80  cab ( a² + b²  + c ² )

Or ( a + b + c ) ⁵ -  ( a + b – c ) ⁵  - ( b + c – a ) ⁵  - ( c + a – b )⁵

On a donc bien : ( a + b + c ) ⁵ -  ( a + b – c ) ⁵  - ( b + c – a ) ⁵  - ( c + a – b )⁵  = 80  cab ( a² + b²  + c ² )