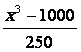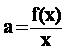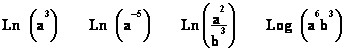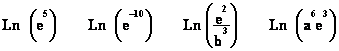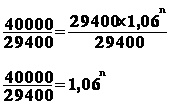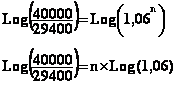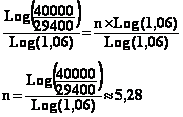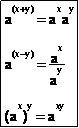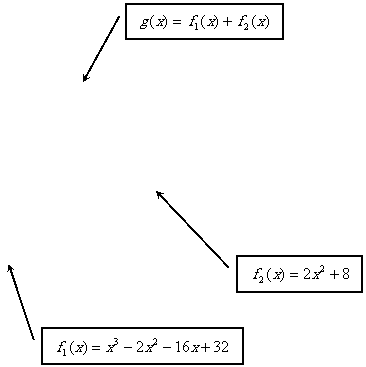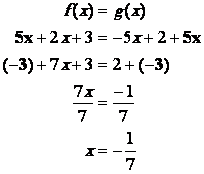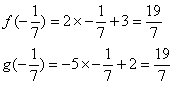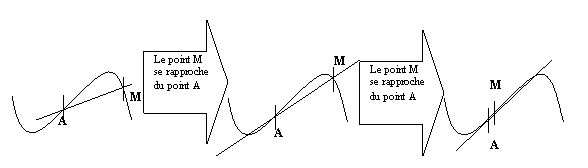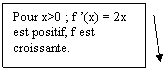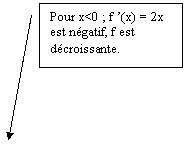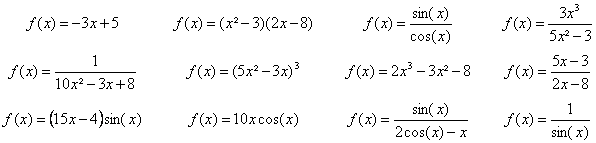LES
FONCTIONS NUMERIQUES
ET
LEURS APPLICATIONS
DEFINITION
D' UNE FONCTION NUMERIQUE -VOCABULAIRE
En
mathématique, une fonction numérique est un lien entre deux ensembles de
nombres.
Exemple : On décide d'associer à tout
nombre x, le double de celui-ci. Le nombre associé est fonction de x, on le
note (x).
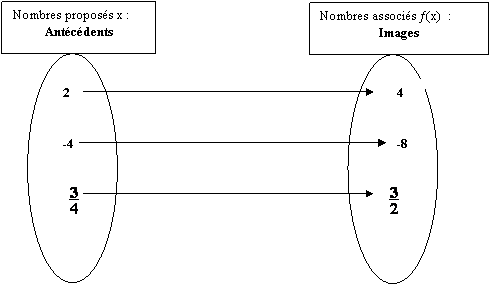
Le
diagramme précédent est appelé diagramme sagittal de la fonction
Les nombres
de l'ensemble de départ sont appelés antécédents.
Les nombres
de l'ensemble d'arrivé sont appelés images.
On note
cette fonction : : x ® 2x : il faut lire : " fonction
¦ qui a tout nombre x associe le nombre 2x."
L'expression
algébrique de la fonction est : (x) = 2x
FExercices
1°) Donner
l'expression algébrique de la fonction g qui a tout nombre x associe la moitié
de celui-ci.
2°)
Construire le diagramme sagittal de la fonction g pour les antécédents : -2 ; 0
; 7 ; 9.
3°) Soit la
fonction : x ® 2x -5; calculer les images des nombres 8 ;
5 ; 7 ; 13 ; 0 ; -1 ; -2.
4°) Donnez
l'expression algébrique de la fonction h suivante : "Je prends un nombre
x, je le divise par 2, j'ajoute 5 au résultat.
Votre
calculatrice regorge de fonctions numériques celles-ci sont représentées par
les touches
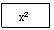
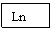



 Le fonctionnement de ces touches
dépend du modèle de la calculatrice.
Le fonctionnement de ces touches
dépend du modèle de la calculatrice.
Les deux
types de fonctionnement sont illustrés à l'aide de la touche : Cette touche représente la fonction
"sinus",
iVérifier que votre calculatrice est
réglée sur le mode DEG (affiché en haut ou en bas de l'écran)
On veut
calculer l'image de 5 par la fonction sinus, il existe deux fonctionnements de
calculatrice :
Fonctionnement direct
La séquence
de touches est la suivante :


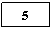
La
calculatrice affiche le résultat :
0.087155743
Fonctionnement
indirect
La séquence
de touche est la suivante :
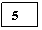
La
calculatrice affiche le résultat :
0.087155743
FExercices
En
utilisant votre calculatrice, compléter le tableau suivant :
|
x
|
10
|
15
|
20
|
25
|
30
|
45
|
92
|
185
|
275
|
|
1(x)=Cos(x)
Arrondir
à 0,001 si nécessaire
|
|
|
|
|
|
|
|
|
|
|
2(x)=x²+6
|
|
|
|
|
|
|
|
|
|
|
3(x)=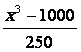
Arrondir
à 0,001 si nécessaire
|
|
|
|
|
|
|
|
|
|
REPRESENTATION
GRAPHIQUE D' UNE FONCTION NUMERIQUE
Pour
représenter graphiquement une fonction numérique , on construit d'abord
un tableau à simple entrée regroupant les valeurs de x et de leurs
images (x)
Ensuite on
place les points de coordonnées (x ; y=(x)) dans un repère dont les
axes sont orthogonaux.
L'ensemble
de ces points forme la représentation graphique de la fonction
Exemple : On désire construire la
représentation graphique de la fonction g : x ®
x² pour des valeurs
de x comprises entre -4 et 4 et variant par pas de 0,5
u On construit le tableau de valeurs
:

v On construit la courbe
représentative dans un repère dont l'échelle des 2 axes est adaptée aux données
:
En abscisse on représente les
valeurs de x
En ordonnée on représente les
valeurs de g(x)
 Les coordonnées des points sont ( x
; g(x) ) ; dans ce cas il y a 17 points
à placer sur le graphique.
Les coordonnées des points sont ( x
; g(x) ) ; dans ce cas il y a 17 points
à placer sur le graphique.
FExercice
On
considère la fonction g : x ® x3.
1°)
Construire un tableau de valeurs pour des valeurs de x allant de -2 à 2 par pas
de 0,1
2°)
Construire la représentation, graphique de cette fonction en choisissant comme
unité graphiques :
1 cm pour 0,5 unités en abscisse
1 cm pour 1 unité en ordonnée
ETUDE
DE QUELQUES FONCTIONS PARTICULIERES
uLES FONCTIONS LINEAIRES
Définition Lorsque qu'à chaque nombre x, on associe le nombre ax (a est un nombre quelconque différent de
zéro), on défini une fonction
linéaire de coefficient a.
On note cette fonction : x ®
ax.
Exemple : Soit la fonction linéaire de
coefficient « -3 » . A chaque nombre « x » on associe le nombre « -3.x »
Le tableau
suivant regroupe quelques images de nombres pour cette fonction.
Remarques :
·
Les suites de nombres x et (x) forment deux
suites de nombres proportionnelles. a est le coefficient de
proportionnalité.
·
Pour déterminer la valeur du coefficient a, il faut
calculer le rapport (x) sur x : 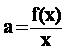
FExercices
1°) Une
pompe distribuant du carburant est une machine permettant de fabriquer des
fonctions linéaires
Au moment
où l'on prend du GPL son prix au litre
est 0,92 .
a)Compléter le tableau de valeurs suivant
|
Nombre
de litres( L)
|
1
|
10
|
25
|
47,5
|
|
x
|
|
Prix
total à payer ( )
|
|
|
|
|
40
|
|
b)On défini la fonction linéaire f telle qu'au nombre de
litres x on associe le prix total à payer f(x). Donner l'expression algébrique
de la fonction f.
c) Représenter graphiquement la fonction f
2°)
Complétez les tableaux de valeurs et représentez graphiquement chaque fonction
f et g
|
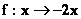
|
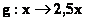
|
|
Tableau
de valeurs
|
Tableau
de valeurs
|
Représentation
graphique

|
Représentation
graphique

|
|
L'équation
de la droite représentative de la fonction f
est :
|
L'équation
de la droite représentative de la fonction g est :
|
D'après les exercices précédents on constate que la
représentation graphique d'une fonction linéaire : x ® ax est une droite qui passe par
l'origine du repère.
L'équation de cette droite est y = ax. a est le
coefficient directeur de la droite.
Remarque :
·
Quand deux grandeurs sont proportionnelles, l'une est une
fonction linéaire de l'autre.
·
En pratique pour tracer la droite déquation y = ax, on
calcule les coordonnées dun point pour une valeur de x que lon choisi et on
trace la droite entre ce point et lorigine du repère.
FExercices
1°)
L'intérêt I d'un placement au taux de 4,5 % par an est proportionnel au capital
C placé.
a) Calculer les intérêts
rapportés par 300 , 500 , 1000 , 2000 .
b) Exprimez I en fonction
de C.
c) Cette situation
peut-elle être représentée par une fonction linéaire ? Si oui donner le
coefficient de cette fonction.
2°)
Calculer les coefficients des fonctions linéaires f et g suivantes sachant que
leur représentation graphique est une droite passant par l'origine du repère et
:
le point A
(1 ; 3 ) pour la fonction f
le point
B(-2;5) pour la fonction g
3°) a) Complétez le tableau suivant :
|
Fonction
|
Equation
de la droite représentative
|
Coefficient
directeur de la droite
|
Tableau
de valeurs
|
|
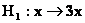
|
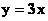
|
3
|
|
|
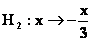
|
|
|
|
|

|
|
|
|
|
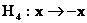
|
|
|
|
b) Construire sur le même
graphique les représentations graphiques de ces 4 fonctions :
vLES FONCTIONS AFFINES
Définition Lorsque qu'à chaque nombre x, on associe le nombre ax + b (a et b sont des nombres quelconques
différents de zéro), on défini une fonction
affine.
On note cette fonction : x ®
ax + b
Exemple : La fonction : x ®
2x - 3 une fonction
affine. Le tableau ci-dessous regroupe quelques images de x par cette fonction
:
|
x
|
0
|
-2
|
1
|
5
|
10
|
|
(x)
|
-3
|
-7
|
-1
|
7
|
17
|
La représentation graphique de cette fonction est :
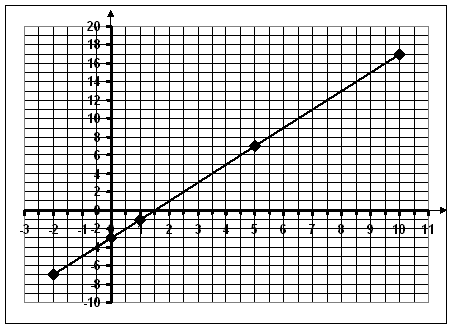
C'est une
droite d'équation y = 2x -3, cette droite ne passe pas par l'origine du repère.
La représentation graphique d'une fonction affine :
x ® ax + b est une droite d'équation y = ax + b.
FExercices
1°)
Calculer les images des nombres 5 ; 8 ; 0 ; -2 ; 10 ; 15 ; 12 ; 13 ; -2.5 ; 4
des fonctions suivantes ; Regrouper les résultats dans un tableau à simple
entrée.
: x ®
4x-2
g : x ®
10 x - 3
h : x ®

2°) Un
garagiste ayant dépanné un véhicule sur le bord de la route établit sa facture
en utilisant les éléments suivants :
- 30 de l'heure en main d'uvre
- 45 de frais de déplacement
Complétez le tableau suivant :
|
Nombre
d'heure de travail
|
1h
|
3h
|
..
|
x
|
|
Prix
de la main d'uvre
|
|
|
|
|
|
Frais
de déplacement
|
|
|
|
|
|
Total
à payer
|
|
|
300
|
|
On appelle
f la fonction qui à un nombre d'heures de travail x associe le prix total à payer f(x)
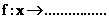
Tracez la
représentation graphique de f.
3°) Le
mouvement dun chariot automatisé est donné par le diagramme ci-dessous, où x
représente la position du chariot et t le temps :
a)
Déterminer à laide du graphique la vitesse du chariot dans
chaque phase du mouvement.
b)
Chaque segment de droite représente une fonction x(t).
Donner lexpression algébrique de chaque fonction pour chacune des phases du
mouvement.
4°) Le
diagramme ci-dessous est la représentation graphique de la fréquence de
rotation n (tr/min) du vilebrequin en fonction de la vitesse v en km/h, pour
chaque rapport de boîte
1°) Quel
type de fonctions représente chaque droite ?
2°)
Déterminer le coefficient directeur de chaque droite ; En déduire
lexpression algébrique de chaque fonction n(v).

SENS DE VARIATION, TABLEAU DE VARIATION
Une fonction f est croissante sur un intervalle de x
donné si x augmente alors f(x) augmente.
Une fonction est décroissante sur un intervalle de x
donné si x augmente alors f(x) diminue.
Pour une
fonction donnée on représente ces variations dans un tableau à double entrées,
la première ligne de ce tableau regroupe par ordre croissant les valeurs de x
qui correspondent à un changement de sens de variation de f. Sur la seconde
ligne du tableau on représente les variations de la fonction par des flèches
montantes ( pour la croissance de f) ou descendantes ( pour la décroissance de
f) ainsi que les valeurs prises par la fonctions aux valeurs de x relevées dans
la première ligne du tableau.
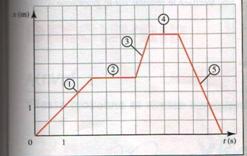
Exemple : Soit la représentation graphique
dune fonction f suivante :
Le Tableau
de variation de cette fonction est :
|
x
|
-2 -1 2 4
|
|
Variation de f
|
   3 4 3 4
2
-1
|
La fonction
f est croissante sur [-2 ; -1 ]
La fonction
f est décroissante sur [-1 ; 2]
La fonction
f et croissante sur [ 2 ; 4 ]
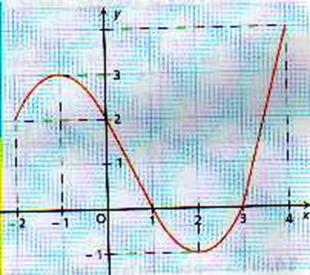
FExercices
Dresser le
tableau de variation de la fonction suivante dont la représentation graphique
est donnée ci-dessous :
Sur quels
intervalles de x la fonctions est-elle croissante ?
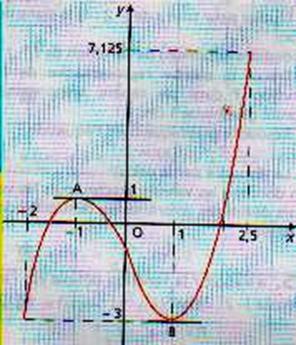 Quelle est la valeur de f(0) ?
Quelle est la valeur de f(0) ?
LES AUTRES FONCTIONS USUELLES
§
Les fonctions du second degré
Lexpression
algébrique dune telle fonction est de la forme f(x) = a x² + bx + c (où a, b
et c sont des réels et a est non nul). La représentation graphique est une
parabole.
Cas où a > 0

On constate
que lorsquon calcule des images pour des valeurs de x très grandes (positives
ou négatives) alors f(x) devient très grand également. On dit que f tend vers
plus linfini lorsque x tend vers plus ou moins linfini.
On
note :
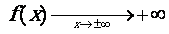
Cas où a < 0
De la même
façon :

FExercice
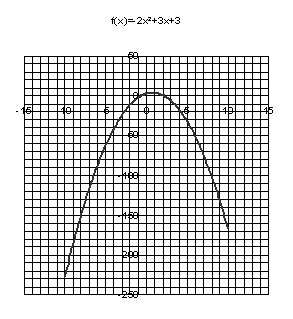
Un
restaurant a réalisé une étude théorique prévisionnelle du bénéfice rapporté
pour une période donnée par les banquets.
Ce bénéfice
est donnée en par :
B(x)=-80 x²+ 2 400x 10000 où
x représente le nombre de banquets organisés.
1°)
Reproduire et compléter le tableur suivant :
|
X
|
4
|
5
|
10
|
12
|
15
|
18
|
25
|
26
|
|
B(x)
|
|
|
|
|
|
|
|
|
2°)
Représenter graphiquement la fonction B pour 4 < x < 26
Unités
graphiques : abscisse : 1 cm pour 4, Ordonnée : 1 cm pour
1 000
3°)
Déterminer graphiquement :
a) Pour combien de
banquets le restaurant réalise un bénéfice positif
b) Le nombre de banquets
pour lequel le bénéfice est maximal. Quel est ce bénéfice ?
§
La fonction racine carrée
La fonction
est définie seulement pour x>0. Son expression algébrique est : 
Sa
représentation graphique est :

§
Les fonctions inverses
Ce sont des
fonctions du type 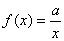 avec a non nul. Elles sont définies pour tous x différents de
zéros ( limage de zéro nexiste pas ).
avec a non nul. Elles sont définies pour tous x différents de
zéros ( limage de zéro nexiste pas ).
Si a
> 0
On constate
que si on calcule des images pour des valeurs de x sapprochant de 0 par
valeurs négatives alors f(x) devient un nombre négatif très grand. On dit que f
tend vers moins linfini ( notation « - ¥ ») lorsque x tend vers 0-.
On note ceci de la façon suivante ;

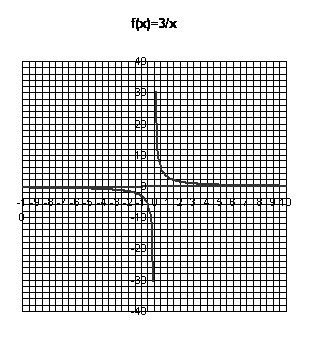
Graphiquement
la courbe se rapproche de laxe des ordonnées sans jamais le toucher, on dit
que laxe des ordonnées est une asymptote.
De la même
façon, on constate que si on calcule des images pou des valeurs de x
sapprochant de 0 par valeurs positive alors f(x) devient un nombre positif
très grand. On dit que f tend vers plus linfini ( notation « + ¥ »)
lorsque x tend vers 0+. On note :
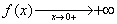
Lorsque
lon calcule des images de f pour des valeurs de x très grandes, on constate
que f(x) se rapproche de zéro par valeurs positives, on dit que f(x) tend vers
zéros plus lorsque x tend vers plus linfini.
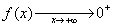
Graphiquement,
la courbe de f se rapproche de laxe des abscisses par le dessus sans jamais le
toucher.
Lorsque
lon calcule des images de f pour des valeurs de x très grandes négatives, on constate
que f(x) se rapproche de zéro par valeurs négatives, on dit que f(x) tend vers
zéros moins lorsque x tend vers moins linfini.

Graphiquement,
la courbe de f se rapproche de laxe des abscisses par le dessous sans jamais
le toucher.
La
représentation graphique est :
Si a
< 0
On constate
les conclusions inverses des précédentes :
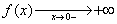
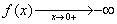
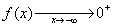
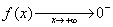
 Graphiquement on obtient :
Graphiquement on obtient :
Ces types
de courbes sont appelés des hyperboles.
FExercice
Etablir les
tableaux de variation des fonctions précédentes.
FONCTIONS
LOGARITHMES ET EXPONENTIELLES
I.
FONCTIONS LOGARITHMES
I.1. Fonction logarithme népérien
a) Définition
La fonction logarithme népérien notée "Ln"
est la fonction qui a tout nombre x fait correspondre le nombre Ln(x) = Ln x.
Cette fonction n'est définie que pour x > 0.
Cette fonction s'annule pour x = 1 soit : Ln 1 = 0.
Pour
calculer le logarithme népérien d'un nombre, il faut utiliser la touche Ln de
votre calculatrice. Suivant le modèle deux modes de fonctionnement existent :
Exemple :
On veut calculer le logarithme népérien de 2 soit Ln 2
Fonctionnement direct
La séquence
de touche est la suivante :
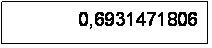 La calculatrice affiche :
La calculatrice affiche :
Fonctionnement indirect
La séquence
de touche est la suivante :
La
calculatrice affiche :
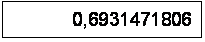
FExercice n°1
A l'aide de
votre calculatrice donnez les valeurs des logarithmes népériens des nombres
suivants (quand cela est possible)
Arrondir les résultats à 0,001 près.
|
x
|
12
|
15,5
|
-8
|
3,14
|
87
|
100000
|
3669,778
|
1475
|
0
|
|
Ln x
|
|
|
|
|
|
|
|
|
|
b) Propriétés
opératoires
Pour tout
nombre a et b strictement positifs on a :

Ainsi, la
fonction Logarithme népérien, transforme une multiplication en une addition et
une division en une soustraction.
FExercice n°2
En
utilisant les propriétés opératoires de la fonction Ln, exprimer en fonction de
Ln (a) et Ln (b) les nombres suivants :
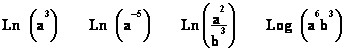
c) Définition du nombre
e
Le nombre e est tel que Ln e = 1. Sa valeur est e »
2,718281828
.
Pour avoir
la valeur de e à l'aide de votre calculatrice il faut procéder à la séquence de
touches suivantes :
Fonctionnement direct

Fonctionnement indirect
FExercice n°3
En
utilisant les propriétés opératoires de Ln et celle du nombre e calculer
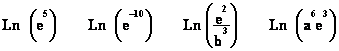
d) Représentation
graphique de la fonction Ln
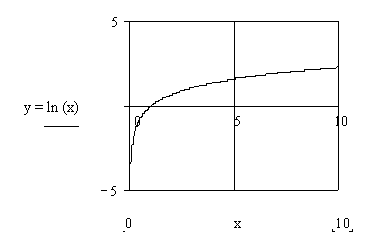
La
représentation graphique de la fonction Ln, constitué des points de coordonnées
(x ; y=Ln x ).
Elle passe
par le point de coordonnées ( 1 ; 0 ) , puisque Ln 1 = 0.
Elle passe
également par le point de coordonnées ( e ; 1 ) puisque Ln e = 1.
Quand x
devient très grand ( valeurs positives) alors Ln x devient très grand
également. On dit que Ln x tend vers plus l'infini (on note + ∞) quand x
tend vers plus l'infini ( On note - ∞).
Quand x
devient très petit, (il s'approche de plus en plus de zéro ) , Ln x devient
très grand dans les valeurs négatives :
On dit que Ln x tend vers moins l'infini (on note - ∞ ) quand x tend vers
zéro ( car Ln 0 n'existe pas )
Le tableau
de variation de cette fonction est :
|
Valeurs de x
|
0 +
∞
|
|
Sens de variation de Ln x
|
|
On met une
double barre en dessous du zéro pour montrer que la fonction Ln n'est pas
définie pour x = 0.
|
La
fonction Ln est une fonction strictement croissante donc :
Si a = b alors Ln(a) = Ln (b)
Si a >b alors Ln (a) > Ln
(b)
Si a < b alors Ln (a) < Ln
(b)
|
I.2. Fonction logarithme
DECIMAL
a) Définition
Elle est définie à partir de la fonction Ln par :  pour
x > 0
pour
x > 0
Pour
calculer la valeur du logarithme décimal d'un nombre, on utilise la touche Log
de la calculatrice. Le principe de fonctionnement est le même que pour la
fonction Ln.
b) Propriétés
opératoires
Les propriétés opératoires sont les mêmes que la
fonction Ln.
Deux propriétés supplémentaires qui découlent de la
définition sont : Log (10) = 1 et Log ( 10x ) = x
En effet :  et
et 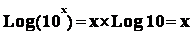 car Log 10 = 1.
car Log 10 = 1.
FExercice n°4
Sans
utiliser votre
calculatrice, compléter le tableau suivant :
|
x
|
102
|
10-5
|
108
|
10-5,7
|
10-12,7
|
1099
|
10-37,5
|
103
|
101
|
|
Log x
|
|
|
|
|
|
|
|
|
|
c) Représentation
graphique de la fonction Log
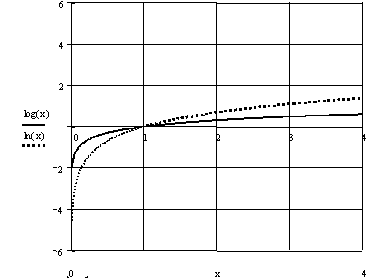 Puisque Ln 10 > 0, Le tableau de variation de la fonction
Log est le même que celui de la fonction Ln.
Puisque Ln 10 > 0, Le tableau de variation de la fonction
Log est le même que celui de la fonction Ln.
La courbe
représentative est similaire.
La fonction
Log est une fonction croissante. Sur ce graphique sont tracées les deux
représentations graphiques des deux fonctions.
De plus on
remarque que :
Pour x
> 1, Log (x ) > 0 et Ln (x) > 0
Pour x
< 1, Log (x) < 0 et Ln(x) < 0
Le tableau
de variation de la fonction Log est :
|
Valeurs de x
|
0 +
∞
|
|
Sens de variation de Log x
|
|
I.3. UTILISATION DES FONCTIONS LOGARITHMES
On utilise
ces fonctions pour résoudre des équations dans lesquelles l'inconnue est un
exposant.
Exemple La valeur acquise Cn
d'un capital C placé à intérêts composés au taux t annuel pendant n années est
donné par la relation :
Cn = C (1 + t )n
On veut
déterminer au bout de combien d'années n
la valeur acquise Cn un capital de 29 400 placé à 6 %
vaudra 40 000 .
La première
étape consiste à remplacer dans la relation donnée les grandeurs que l'on
connaît :
A savoir C
= 29 400 t = 0,06 Cn = 40 000
La relation
devient avec ces valeurs :
40 000 = 29 400 ( 1 + 0,06 )n
40 000 = 29 400 ´
1,06n
On veut
déterminer la valeur de n, il faut donc dans un premier temps isoler dans le
membre de droite 1,06n en divisant les deux membres de l'équation
par 29 400 :
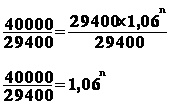
C'est à
partir de cette équation que l'on va se servir des propriétés opératoires des
fonctions logarithmes.
On prend le
logarithme décimal ( ou népérien peut importe car elles ont les mêmes
propriétés opératoires) des deux membres :
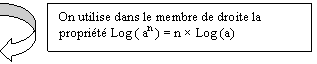
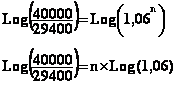
On peut
maintenant diviser les deux membres de l'équation par Log(1,06) afin d'isoler n
et d'en déterminer ainsi la valeur.
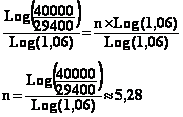
Il faut
donc environ 5,28 années soit 5 ans et 3 mois et 11 jours environs.
FExercice n°5
Un capital
de 2 500 est placé à intérêts composés au taux annuel de 5 %.
1°)
Calculer la valeur acquise par le capital au bout de 4 ans.
2°)
Calculer le nombre d'année de placement nécessaires pour obtenir une valeur
acquise de 4 275,85 .
I.
>>FONCTIONS
EXPONENTIELLES
II.1. FONCTION
EXPONENTIELLE DE BASE e
a) Définition
On appelle fonction exponentielle de base e, la
fonction qui a x fait correspondre ex. Elle est définie pour tout
nombre x.
NB : On
rencontre parfois également la notation exp(x)
Pour
calculer la valeur de l'exponentielle d'un nombre, on utilise la touche ex
de la calculatrice. De même que pour la fonction Ln, il existe deux modes de fonctionnement :
Exemple : On veut calculer l'exponentielle
de 2,5 soit e2,5
Fonctionnement
direct
La séquence
de touche est la suivante :

La
calculatrice affiche le résultat :

Fonctionnement
indirect
La séquence
de touche est la suivante :
La
calculatrice affiche le résultat :
FExercice n°6
A l'aide de
votre calculatrice, calculez complétez le tableau suivant ( Arrondir à 0,001
près )
rrrererererere
b) Propriétés
opératoires
Quels que
soient les nombres x et y on a :

L'exponentielle
transforme une somme en produit.
Elle
transforme une différence en quotient.
Une
propriété importante est que les fonctions Logarithme népérien et exponentielle
sont des fonctions réciproques
Leurs
effets sur un nombre x "s'annulent" mutuellement.
En effet :
eln 3 = 3 Ln
(e3) = 3
D'une manière plus générale pour
tout nombre x : Ln (ex ) = x et si x > 0 eLn(x) = x
c) Représentation
graphique
La
représentation graphique de la focntion exponentielle est constituée des points
de coordonnées ( x ; y = ex)
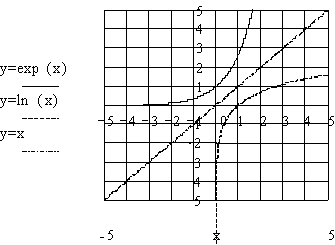 La réciprocité des deux fonctions logarithmes népérien et
exponentielle impliquer une symétrie par rapport à la première bissectrice
(droite d'équation y = x ) des courbes représentatives des deux fonctions :
La réciprocité des deux fonctions logarithmes népérien et
exponentielle impliquer une symétrie par rapport à la première bissectrice
(droite d'équation y = x ) des courbes représentatives des deux fonctions :
La fonction
exponentielle est également une fonction croissante.
Lorsque x
devient très grand ( on dit qu'il tend vers + ∞ ), ex devient
très grand également ( ex tend vers + ∞).
Lorsque x
tend vers des valeurs négatives très grandes, ex devient nulle. On
dit que lorsque x tend vers -∞ alors ex tend vers zéro.
Des
constatations précédentes on peut établir le tableau de variations suivant
:
|
Valeurs de x
|
- ∞ +
∞
|
|
Sens de variation de ex
|
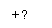  
|
Puisque la
fonction exponentielle est une fonction croissante on a donc les propriétés
suivantes :
Si x = y alors ex = ey
Si x > y alors ex >
ey
Si x < y alors ex <
ey
II.2. FONCTIONS
EXPONENTIELLES DE BASE a
a) Définition
On appelle fonction exponentielle de base a (a > 0
et différent de 1), la fonction qui a x fait correspondre ax. Elle
est définie pour tout nombre x.
Exemple la fonction exponentielle de base 3
est définie par 3x.
Pour
calculer 3x pour x = 1,5 on utilise la touche puissance de la
calculatrice (en général notée yx)
Ainsi 31,5 = 5,196152
.
b) Propriétés
opératoires
Mais
pourquoi dit-on "fonction exponentielle de base a" ? En effet,
derrière le ax se "cache" une exponentielle :
Posons : y
= ax de façon à avoir une égalité.
Prenons les
logarithmes népériens des deux membres de l'égalité précédente :
Ln(y) = Ln (ax)
En
utilisant dans le membre de droite une propriété opératoire de Ln on a :
Ln(y) = x ´
Ln (a)
Prenons
l'exponentielle de chaque membre :
eLn(y) = ex´Ln(a)
Or eLn(y)
= y, l'égalité devient : y = ex´Ln(a)
Or au
départ on a posé y = ax donc ax = ex´Ln(a)
Il faut
donc retenir que :
ax = ex ´ Ln(a)
C'est la
raison pour laquelle on dit que ax est une fonction exponentielle de
base a.
Les
propriétés opératoires sont les mêmes que pour les exponentielles de base e :
FExercice n°7
Résolvez
les équations suivantes :
3 x = 2 4 x = 5 2 x = 3 2 x+1 = 3
Indication : il faut prendre le logarithme de
chaque membre et utiliser les propriétés opératoires des logarithmes
SOMME
DE FONCTIONS-PRODUIT DUNE FONCTION PAR UNE CONSTANTE
Somme de deux fonctions
La somme de
deux fonction f1 et f2 est aussi une fonction g telle que
g(x)=f1(x)+f2(x).
Pour
obtenir la courbe de g lorsque les courbes de f1 et f2
sont tracées sur un même graphique, il suffit pour chaque abscisse x
dadditionner les ordonnées des deux fonctions f1 et f2
correspondantes.
Exemple
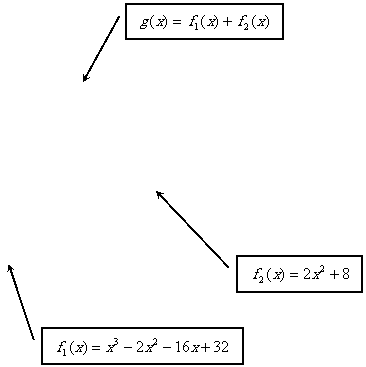
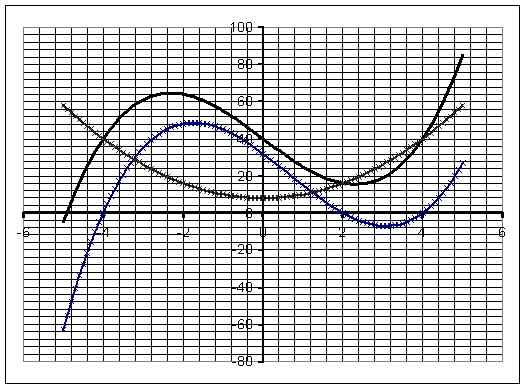
FExercice
Un responsable dentreprise a établi que le coût total de
fabrication se décompose en charges variables te en charges fixes exprimées en
par les relations :
Charges variables : C1(x)=2x²+10x
Charges fixes : C2(x)=1 500 où x
représente le nombre darticles.
1°) Représenter dans un repère orthogonal les fonctions f1
et f2 définies sur lintervalle [ 0 ; 40 ] par :
f1(x)=2x²+10x f2(x)=
1 500
Unités graphiques :
Abscisses : 1 cm pour 5 unités, Ordonnée : 1 cm pour 500
unités.
2°) Construire la courbe représentative de la fonctions f1
+ f2 à partir des représentations précédentes .
Produit dune fonction par une
constante
Le produit
dune fonction f par une constante a non nulle est une autre fonction g telle
que :
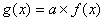
Pour obtenir
la courbe de g à partir de celle de f il suffit pour chaque abscisse x de
multiplier lordonnée correspondante de f par a.

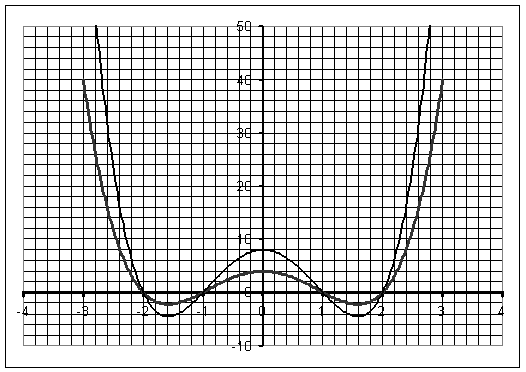
FExercice
Tracer la
courbe représentative de la fonction 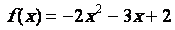 sur lintervalle [-10 ; 10]. En déduire la courbe
représentative de la fonction
sur lintervalle [-10 ; 10]. En déduire la courbe
représentative de la fonction 
RESOLUTION
GRAPHIQUE DE L EQUATION 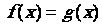
Résoudre
léquation 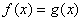 consiste à trouver les valeurs de x pour lesquelles cette
égalité est vraie.
consiste à trouver les valeurs de x pour lesquelles cette
égalité est vraie.
Lorsque les
fonctions f et g sont des fonctions affine ou linéaire, léquation est du
premier degré, on peut donc la résoudre par le calcul. Voyons avec deux de ces
fonctions la relation entre la solution que lon peut calculer et le
graphique :
Prenons par
exemple 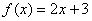 et
et 
Résolution par le calcul
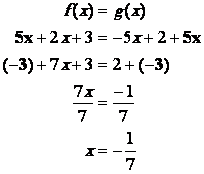
La solution exacte de léquation 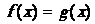 est
est 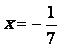
Vérifions
que f et g sont égales pour cette valeur de x :
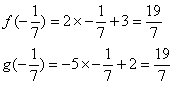
Légalité est vérifiée
 On a
On a 
Résolution graphique
Le problème
est quil faut déjà avoir une idée de la valeur de la solution pour pouvoir
tracer les fonctions sur un certain intervalle de x, on sait que la solution
est proche de zéros donc on va tracer les deux droites pour x compris entre -1
et 0 par pas de 0,01.
On trace
donc les courbes représentatives de f et g qui sont des droites. Le point
dintersection correspond au cas où 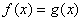 .
.
Labscisse
du point correspond à la solution ( ici il ny en a quune), lordonnée
correspond à la valeur prise par les deux fonctions.
On a donc
approximativement comme coordonnées ( -0,14 ; 2,7)
La solution approchée de léquation est x=-0,14

Conclusion : Pour résoudre graphiquement une
équation du type 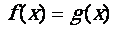 Il suffit de tracer les courbes représentatives
des deux fonctions f et g et de relever les abscisses des points dintersection
des deux courbes
Il suffit de tracer les courbes représentatives
des deux fonctions f et g et de relever les abscisses des points dintersection
des deux courbes
Remarque : Lune des deux fonctions
peut être une constante, dans ce cas légalité est 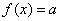 , les solutions de ce type déquations correspondent donc
aux abscisses des points dintersection de la courbe représentative de f avec
la droite déquation y = a qui est une droite horizontale.
, les solutions de ce type déquations correspondent donc
aux abscisses des points dintersection de la courbe représentative de f avec
la droite déquation y = a qui est une droite horizontale.
FExercice
1°)On
considère la fonction : 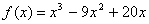
a) En utilisant une calculatrice, compléter le tableau
suivant :
b) Tracer la courbe représentative de cette fonction avec
comme unités graphiques :
Abscisse :
1 cm pour 1 unité
Ordonnée :
1 cm pour 2 unités
Il faut
recalculer des images pour avoir un tracé plus exact !!!
c) Résoudre graphiquement léquation f(x) = 0
RESOLUTION
GRAPHIQUE DUNE INEQUATION ENTRE DEUX FONCTIONS
Considérons
deux fonctions 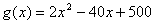 et
et  , il sagit de trouver les valeurs de x pour lesquelles
, il sagit de trouver les valeurs de x pour lesquelles 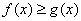 . Graphiquement
. Graphiquement 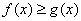 est réalisée lorsque la courbe représentative de f est au
dessus de celle de g et lorsque les deux courbes coïncident.
est réalisée lorsque la courbe représentative de f est au
dessus de celle de g et lorsque les deux courbes coïncident.
Cela
correspond à la partie du graphique comprise entre x=5 et x=20. Lensemble des
solutions de linéquation 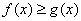 est [ 5 ; 20
]
est [ 5 ; 20
]

NB :
Lensemble des solutions de linéquation  est ] 5 ; 20
[ car linégalité est stricte et on ne tient pas compte de légalité entre les
deux fonctions.
est ] 5 ; 20
[ car linégalité est stricte et on ne tient pas compte de légalité entre les
deux fonctions.
FExercice
Dans cet
exercice, on se propose détudier la rentabilité dune production.
1°) On
considère la fonction C définie sur lintervalle [0 ;25] par :
C(x)=2x²-40x+500
a) Calculer C(0) ;
C(5) ; C(10) ; C(15) ; C(20) ; C(25)
b) Représenter
graphiquement cette fonction.(abscisses 1 cm pour 2 unités, ordonnée : 1
cm pour 50 unités)
2°) On
considère la fonction P définie sur [ 0 ; 25 ] par
P(x)=10x+30
Représenter
graphiquement cette fonction dans le repère précédent.
3°) Le coût
de production dun produit est donné par la relation :
C(q)=2q²-40q+500 où q est la
quantité produite.
Le prix de
vente est donné par la relation :
P(q)=10 q + 300
a) En utilisant les
résultats précédents, déterminer graphiquement pour quelles valeurs de q le
prix de vente est égal au coût de production.
b) Sur quel intervalle la
production est-elle rentable ?
NOMBRE
DERIVE-DERIVEE DUNE FONCTION NUMERIQUE
Nombre dérivé
Par définition, le nombre dérivé dune fonction f au
point dabscisse x0, est égal au coefficient directeur de la
tangente à la courbe au point dabscisse ( x0 ; f(x0)).
Le nombre dérivée est noté f (x0). (Lire
f prime de x0)
La tangente
est une droite introduite pour caractériser la pente directrice dune courbe
(C), associée à une fonction f.
Géométriquement,
la tangente à une courbe (C) au point A d'abscisse x0, est la droite
« position limite » de la droite (AM) lorsque M tend vers A, M étant un point
quelconque de (C).
Regardez la
séquence de dessin ci-dessous, plus le point M se rapproche du point A, plus la
droite dessinée devient la tangente à la courbe au point A :
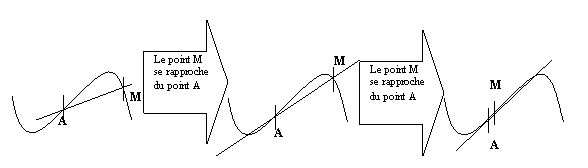
Dans cette
partie vous allez voir comment de déterminer par le calcul, le coefficient directeur
de la tangente à la courbe représentative de la fonction f(x)=x²
Nous allons
faire ce travail au point dabscisse A :
x0 = 3. Les coordonnées de A sont donc A(x0 ;
f(x0)) soit A(2 ;4). Nous allons prendre un point M(x1 ;
f(x1)) sur la courbe dabscisse 4, les coordonnées de M sont donc((x1 ;
f(x1)) soit ( 4 ; 16 ).
Le calcul
du coefficient directeur de la droite (AM) est 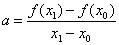 .
.
Le tableau
suivant résume les différentes valeurs
de a lorsque M se rapproche de A :
|
Cordonnées du point A
|
Coordonnées du point M
|
Coefficient directeur de
(AM) : a
|
|
x0
|
f(x0)
|
x1
|
f(x1)
|
|
2
|
4
|
3
|
9
|
5
|
|
2
|
4
|
2.5
|
6.25
|
4.5
|
|
2
|
4
|
2.1
|
4.41
|
4.1
|
|
2
|
4
|
2.0001
|
4.00040001
|
4.0001
|
|
2
|
4
|
2.0000001
|
4.0000004
|
4
|
|
2
|
4
|
2.00000001
|
4.000000004
|
4
|
|
2
|
4
|
2.000000001
|
4.000000004
|
4
|
On constate
que lorsque les deux points sont très proches, la valeur du coefficient
directeur devient constante et égale à 4. On considère alors que la droite (AM)
est la tangente en A à la courbe.
Par
définition, le nombre dérivé de f au point dabscisse x0=2 est 4. On
note : f (2) = 4.
Sur le
graphique ci-dessous, sont représentées la courbe représentative de f(x) = x2
ainsi que les 4 premières droites correspondant aux 4 premiers coefficients
directeurs calculés dans le tableau :

Si on avait
fait le calcul du coefficient de la tangente à la courbe au point A(3 ; 9
) on aurait trouvé 6 ; ainsi par définition f(3) = 6
Pour A
(2 : 4) on a f(2) = 4 = 2 × 2
Pour A
(3 ; 9 ) on a f(3) = 6 = 2 × 3
On peut
remarquer que le nombre dérivée au point dabscisse x0 est à chaque
fois le double ainsi on a alors la formule : f(x0) = 2 x0
.
Cette
formule permet de calculer en nimporte quel point de la courbe le coefficient
directeur de la tangente.
Par exemple
au point A(2,5 ; 6,25) : f(2,5) = 2×2,5 = 5 ( vérifier
graphiquement)
Fonction dérivée
Par définition, la fonction dérivée de f (notée f)
est la fonction qui transforme le nombre x en nombre dérivé de la fonction f au
point dabscisse x.
Ainsi, pour
la fonction f(x) = x2, la fonction dérivée est f(x) = 2x.
A quoi sert
la fonction dérivée dune fonction ?
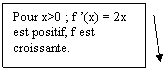
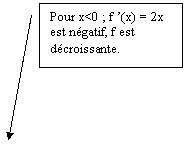 La dérivée dune fonction sert à étudier le sens de
variation dune fonction. En effet, pour x<0, f est décroissante, et f(x) =
2 x < 0 pour tout x <0.
La dérivée dune fonction sert à étudier le sens de
variation dune fonction. En effet, pour x<0, f est décroissante, et f(x) =
2 x < 0 pour tout x <0.
Pour x >
0, f est croisante et f(x) = 2x > 0 pour tout x > 0.
On remarque
que pour x=0, f(x) = 0, en x=0 la courbe représentative de f admet une tangente
horizontale et f est minimale.
On
retiendra :
Pour une fonction f quelconque :
Si f(x) > 0 sur un intervalle de x donné
alors f est croissante sur cet
intervalle.
Si f(x) < 0 sur un intervalle de x donné alors f
est décroissante sur cet intervalle.
Si f(x) = 0 alors f admet une tangente horizontale
et f présente un extremum ( maximum ou minimum)
Ainsi,
maintenant pour connaître le sens de variation dune fonction f on calculera sa
dérivée f, on étudiera ensuite le signe de la dérivée pour en déduire le sens
de variation de f.
Pour
connaître labscisse des extremums dune fonction f il faut résoudre léquation
f(x)=0.
Dérivée des fonctions
numériques usuelles. Calcul de dérivées
Les mathématiciens
ont établis les correspondances suivantes :
|
Fonction f
|
Dérivée f
|
|
x2
|
2x
|
|
x3
|
3x2
|
|
ax+b
|
a
|
|
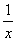
|
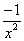
|
|
sin(x)
|
cos(x)
|
|
cos(x)
|
-sin(x)
|
|
u(x) + v(x)
|
u(x) + v(x)
|
|
ku(x)
|
ku(x)
|
|
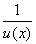
|

|
|
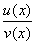
|
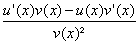
|
|
u(x)v(x)
|
u(x)v(x)+u(x)v(x)
|
|
u(x)n
|
nu(x)u(x)n-1
|
Exemple
de calculs de dérivée de fonctions
§
f(x)=2x+3 f(x)
= 2
§
f(x)=4x² + 3x 2 f(x)
= 8x + 3
§ f(x) = (10x+3)(2x-8) f(x) =
10(2x-8) + (10x+3)2 = 40x 74
§
f(x) = (2x-3)2 f(x)
= 2(2)(2x-3)1=8x - 12
§


F Exercices
1. Calculer la dérivée de
la fonction f dans les cas suivant :
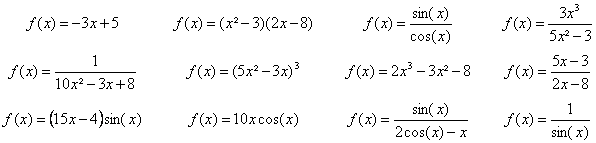
2. Déterminer les
équations des tangentes aux courbes des fonctions ci-dessous au point
dabscisse x0 spécifié entre parenthèses :
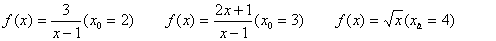
3. Soit la fonction f
définie sur [1,2 ; 9] par : 
a. Calculer la dérivée f
de f
b. Etudier le signe de
f. En déduire le tableau de variation de f
c. Compléter le tableau
de valeurs suivant :
d. Tracer dans un repère
orthonormal ( unité graphique 1 cm) la courbe représentative de f.
e. Tracer dans le même
repère la droite D déquation y=-2x+7. Déterminer graphiquement les coordonnées
des points dintersection de la courbe avec la droite D.
4. Une entreprise
fabrique des jouets quelle vend par lots.
Le coût de fabrication, en euros, dun nombre x de lots est
donné, pour 0≤x≤15 par :
C(x)=4x3-96x²+576x+100
On se propose de déterminer le nombre de lots à fabriquer
pour obtenir le coût minimal.
On considère la fonction f définie sur lintervalle [
0 ; 15 ] par :
f(x)= 4x3-96x²+576x+100
a. Calculer f(x) où f
désigne la fonction dérivée de la fonction f.
b. Vérifier que
f(x)=12(x-4)(x-12)
c. Etablir le tableau de
signe de la dérivée sur [ 0 ; 15 ]
d. En déduire le tableau
de variation de f.
e. Quel est le nombre de
lots à fabriquer pour obtenir n coût minimal. Donner la valeur de ce coût
minimal.
5. Une entreprise
demballages industriels veut réaliser un conteneur ayant la forme dun
parallélépipède rectangle pou un transport maritime à lexportation.
Pour des
raisons techniques, ses dimensions intérieures sont liées par les relations
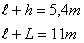
a. Exprimer h et L en
fonction de 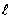 .
.
b. Montrer que le volume
V sexprime, en m3, en fonction de 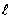 par la relation :
par la relation :
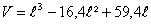
c. Soit f la fonction
définie sur lintervalle [ 1 ; 4 ] par :
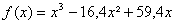
d. Calculer la
dérivée de f
e. Montrer que léquation
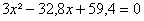 admet deux solutions x1 et x2 que lon
calculera arrondies au centième.
admet deux solutions x1 et x2 que lon
calculera arrondies au centième.
f. Déduire de létude
précédente les dimensions intérieures ( arrondies au cm) du conteneur ayant un
volume maximal.
6. Le service de gestion
dune entrepris a établi que le coût annuel C de son stock, exprimé en euros
est donné en fonction du nombre annuel q de commande par :
 pour q compris entre 2
et 20
pour q compris entre 2
et 20
On
considère la fonction f définie sur lintervalle [ 2 ; 20 ] par :
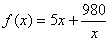
a) Faire un tableau de
valeur de f pour x compris entre 2 et 20 par pas de 4. Donner les résultats
approchés à 0,1 près.
b) Déterminer la fonction
f dérivée de la fonction f.
c) Pour tout x de
lintervalle [ 2 ; 20 ], étudier le signe de f(x), en,déduire le sens de
variation de f.
d) Indiquer la valeur
minimale prise par f(x) pour x appartenant à lintervalle [ 2 ; 20 ]
e) Dans le plan rapporté
à un repère orthogonal, tracer la courbe représentative de f.
Unités graphiques :
abscisses : 0,5 cm pour 1
ordonnée : 1 cm pour 50
f) Indiquer le nombre
annuel de commandes qui permet à lentreprise davoir un coût de stock annuel
minimal.
7. Le circuit électrique
ci-contre comprend :
§
Un générateur
§
Un condensateur
§
Un commutateur
§
Un voltmètre
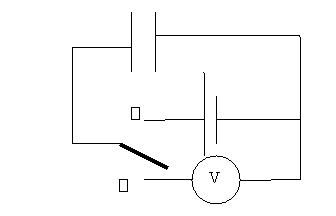 Le condensateur étant préalablement
chargé, (position ), on étudie sa déchargé en fonction
du temps (position )
Le condensateur étant préalablement
chargé, (position ), on étudie sa déchargé en fonction
du temps (position )
Le tableau
ci-dessous donne une série de mesures :
|
t(s)
|
0
|
2
|
4
|
6
|
8
|
10
|
|
U(V)
|
4.5
|
3
|
2
|
1.35
|
0.9
|
0.6
|
a.
Tracer la courbe représentative de la fonction f définie par
f(t)=U dans un repère orthogonal.
La fonction
est-elle linéaire ? affine ? justifier
b. Afin de déterminer la
nature de la fonction f représenter les points de coordonnées (t ; ln U)
dans un repère orthogonal. Quobtenez vous ?
c. Montrer que ln U =
-0,2 t + 1,5. En déduire lexpression de U en fonction de f.