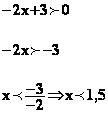CORRECTIONS DES EXERCICES SUR LES NOMBRES DERIVES-FONCTIONS
DERIVEES-UTILISATION
Exercice
n°1
1°)
D'après le formulaire : ¦''(x) = 2x.
Ainsi ¦'(2) = 2´2 = 4
2°)
3°)
 Le nombre dérivée correspond à
la valeur du coefficient directeur de la tangente à la courbe au point
d'abscisse 2 ( point de coordonnées ( 2 ; 4 ) sur la
courbe.
Le nombre dérivée correspond à
la valeur du coefficient directeur de la tangente à la courbe au point
d'abscisse 2 ( point de coordonnées ( 2 ; 4 ) sur la
courbe.
Pour construire cette tangente, on se place au point C( 2; 4 ).
D'une manière générale, le coefficient directeur d'une
droite signifie que lorsque l'abscisse d'un point situé sur la droite augmente
de 1, alors son ordonnée augmente de la valeur du coefficient directeur.
Dans notre cas, la valeur du coefficient directeur de
cette tangente est de ¦'(2)=4.
Pour tracer la tangente, il suffit de partir du point
C de se déplacer de 1 unité vers la droite ( l'abscisse
augmente de 1) et, pour trouver un autre point de la tangente il faut monter de
4 ( l'ordonnée augmente de 4 car 4 est
positif). On utilise ainsi la propriété du coefficient directeur d'une droite
pour la tracer rapidement.
Exercice
n°2
En
utilisant la propriété du coefficient directeur d'une droite, on va déterminer
le coefficient directeur de chacune de ces tangentes.
Graphique
de Gauche
Tangente en A : On se place en A, on se déplace de 1 vers la
droite. Pour retrouver un autre point de la tangente il faut "monter"
de 3 unités : le coefficient directeur de la tangente est 3.
Tangente en B : même raisonnement : A partir de B on se déplace de
1 vers la droite, pour retrouver u point
il faut monter de 0,5 : Le coefficient directeur est 0,5.
Tangente en C : Etant donné la configuration
du graphique, pour déterminer le coefficient directeur l faut ici partir du
point de coordonnée (1;4) de la tangente. Pour retrouver un autre point après
s'être déplacé de 1 vers la droite il faut "descendre de 4 : le
coefficient directeur est -4.
Graphique
de droite
Tangente
en A : Le
coefficient directeur est : -2
Tangente
en B : le
coefficient directeur est : -0,7
Tangente
en C : C'est une tangente
horizontale donc son coefficient directeur est 0.
Exercice
n°3
Fonction
¦(x) = 2x²-8x-5 sur [-5 ; 5 ] ¦'(x) = 4x - 8
Etudions
par exemple pour quelles valeurs de x, 4x - 8 > 0 il faut résoudre cette
inéquation :
 Donc, pour x >2, 4x - 8
> 0 d'où ¦'(x) > 0. Il est évident que si x < 2
alors 4x-8 < 0 d'où ¦'(x) < 0 et que pour x = 2, 4x - 8 = 0 d'où ¦'(x) = 0.
Donc, pour x >2, 4x - 8
> 0 d'où ¦'(x) > 0. Il est évident que si x < 2
alors 4x-8 < 0 d'où ¦'(x) < 0 et que pour x = 2, 4x - 8 = 0 d'où ¦'(x) = 0.
Le tableau
de variation de ¦ est
|
Valeurs de x
|
-5 2 5
|
|
Signe de ¦'(x)
|
Négatif 0 Positif
|
|
Variation de ¦
|
    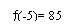
|
Fonction
-x²+3x+5 sur [-2 ; 2] ¦'(x)= -2x + 3
Etudions
par exemple pour quelles valeurs de x, -2x + 3 > 0 il faut résoudre cette
inéquation :
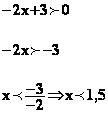
 Donc, pour x <1,5, -2x+3 > 0 d'où ¦'(x) > 0. Il est évident
que si x > 1,5 alors -2x+3 < 0 d'où ¦'(x) < 0 et que pour x = 1,5, -2x+3 = 0 d'où ¦'(x) = 0.
Donc, pour x <1,5, -2x+3 > 0 d'où ¦'(x) > 0. Il est évident
que si x > 1,5 alors -2x+3 < 0 d'où ¦'(x) < 0 et que pour x = 1,5, -2x+3 = 0 d'où ¦'(x) = 0.
Le
tableau de variation de ¦ est
|
Valeurs de x
|
-2 1,5 2
|
|
Signe de ¦'(x)
|
Positif 0 Négatif
|
|
Variation de ¦
|
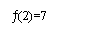 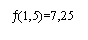   
|
Fonction
x3+x+1 sur [-1 ; 3 ] ¦'(x) = 3x²+1
Il
faut étudier le signe du polynôme du second degré 3x² + 1.
Son
discriminant est D = 0²-4´3´1= -12, il n'y a pas de racines
donc le polynôme est du signe de 3 donc positif ( voir
le signe d'un polynôme du second degré dans le cours correspondant )
On
peut également raisonner de la manière suivante : x² est toujours positif donc
3x² aussi alors 3x² + 1 est positif.
Ainsi
sur [ -1 ; 3 ] ( et pour n'importe quelles valeurs de
x ) , 3x² +1 > 0 donc ¦'(x) > 0
La
fonction x3 + x +1 est croissante sur [-1 ; 3]
|
Valeurs de x
|
-1 3
|
|
Signe de ¦'(x)
|
Positif
|
|
Variation de ¦
|
|
Exercice
n°4
1°) ¦'(x) = 4x-10
2°)
il faut d'abord étudier le signe de ¦'(x) = 4x - 10. Résolvons
l'inéquation 4x - 10 > 0 ( par exemple )
 Pour x > 2,5 on a ¦'(x) > 0 donc la fonction ¦ est croissante.
Pour x > 2,5 on a ¦'(x) > 0 donc la fonction ¦ est croissante.
En
conséquence pour x < 2,5 on a ¦'(x) < 0 donc la fonction ¦ est décroissante.
Le
tableau de variation est
:
|
Valeurs de x
|
0 2,5 4
|
|
Signe de ¦'(x)
|
Négatif 0 Positif
|
|
Variation de ¦
|
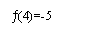 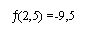 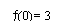  
|
3°) D'après
le tableau de variation, on constate que ¦ admet un minimum pour x = 2,5
et que la valeur de ce minimum est -9,5.
Exercice
n°5
1°)
(x+1)(2x-3) = x´2x + x´(-3) + 1´2x + 1´(-3) = 2x²-3x+2x-3 = 2x²-x-3
2°)
Puisque (x+1)(2x-3) =
2x²-x-3 alors ¦(x) = 2x²-x-3
donc ¦'(x) = 4x-1
Exercice
n°6
1°)
a) D'après le graphique le tableau de variation de ¦ est :
b)
L'équation ¦(x) = 0 se résout
graphiquement en allant lire la valeurs des abscisses des points de la courbe
pour lesquels l'ordonnée vaut 0. Ces points ont pour abscisses -1,5 ; -0,3 ;
1,9.
2°)
a) ¦'(x) = 3x²-3.
Pour
vérifier que ¦'(x) = 3(x-1)(x+1) on va développer
cette expression.
¦'(x)
=3(x²+x-x-1) =3(x²-1) = 3x²-3
|
x
|
-2 -1 1 2,5
|
|
Signe de x-1
|
Négatif 0 Positif
|
|
Signe de x+1
|
Négatif 0 Positif
|
|
Signe de ¦'(x)
|
Positif 0 Négatif 0 Positif
|
b)
c) D'après
le tableau de signe la dérivée ¦' on en déduit que :
Sur
[-2 ; -1 ] ¦ est croissante Sur [-1 ; 1] ¦ est décroissante Sur [1;2,5] ¦ est croissante
Exercice
n°7
Partie
A
1°)
Il faut résoudre l'équation en x : b(x) = 0 0,35x - 45 = 0 d'où x = 45/0,35 ≈ 125,57
2°)
Le bénéfice maximal est donc obtenu pour x = 300 il faut calculer b(300) = 0,35 ´ 300 -45 = 60
Le bénéfice
maximal est de 60 €
3°)
Cette fonction est une fonction affine, sa représentation graphique est une
droite.
Pour
la tracer il suffit d'avoir les coordonnées de deux de ses points pour des
valeurs de x comprises entre [150;300].
Exemple
pour : x = 200 : ¦(200) = 0,35´200-45 = 25 pour x = 250 : ¦(250) = 0,35´250-45 = 42,5
 4°) Il faut aller lire
l'abscisse du point de la droite dont l'ordonnée est 20
4°) Il faut aller lire
l'abscisse du point de la droite dont l'ordonnée est 20
Cette
abscisse est donc x =185.
Partie
B
1°)
On veut que b(300) = 60 soit -0,005´300²+2,6´300+c = 60
330 + c = 60 alors c = -270
Si on
veut que cette condition soit remplie il faut que b(x) = -0,005 x² + 2,6 x
-270
2°)
a)
|
x
|
150
|
180
|
210
|
240
|
260
|
280
|
300
|
|
g(x)
|
7,5
|
36
|
55,5
|
66
|
68
|
66
|
60
|
g(210)
= -0,005 ´ 210²+2,6´210 -270 = 55,5 g(280) =
-0,005 ´ 280²+2,6´280 -270 = 66
b)
g'(x) = -0,005´2x + 2,6 = -0,01 x +2,6
c) Il
faut résoudre l'équation -0,01 x + 2,6 = 0 donc x = -2,6 / -0,01 = 260. on a alors x0 = 260
Cela
signifie que g admet un maximum ou un minimum pour x0 = 260 puisque
la dérivée de g s'annule.
d) il
faut donc calculer b(x0 ) = b (260) =
-0,005´260²+2,6´260 -270 = 68.
Le
bénéfice maximal est de 68 €
 Le nombre dérivée correspond à
la valeur du coefficient directeur de la tangente à la courbe au point
d'abscisse 2 ( point de coordonnées ( 2 ; 4 ) sur la
courbe.
Le nombre dérivée correspond à
la valeur du coefficient directeur de la tangente à la courbe au point
d'abscisse 2 ( point de coordonnées ( 2 ; 4 ) sur la
courbe.