Exercices
sur les nombres dérivés -Fonctions dérivées -Utilisation
Exercice
n°1
On
considère la fonction ¦ définie sur l'intervalle [ -5 ; 5 ] par ¦(x) = x²
On note
C sa courbe représentative dans un repère orthonormal d'unité graphique 1 cm.
1°)
Donner l'expression ¦'(x) de la fonction dérivée ¦' de ¦. En déduire le nombre dérivé ¦'(2)
2°)
Placer dans le repère indiqué le point A de C d'abscisse 2 . En utilisant le
résultat précédent, construire la tangente à C en A.
3°)
Tracer la courbe C
Exercice
n°2
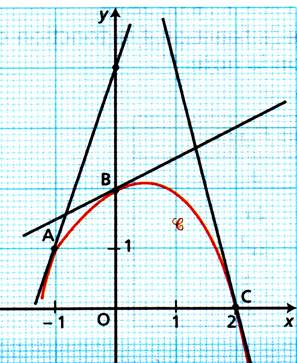
Dans
chacune des figures suivantes, la courbe C est la courbe représentative d'une
fonction ¦.
Sachant
que les droites tracées sont les tangentes à C aux points A, B et C, déterminer
par lecture graphique les nombres dérivés ¦'(-1) , ¦'(0), ¦'(2).
Exercice
n°3

Pour
chacune des fonctions suivantes, Calculer ¦'(x), étudier sur l'intervalle
proposé le signe de ¦'(x) et dresser le tableau de variation de ¦.
¦ définie sur [ -5 ; 5 ] par : ¦(x) = 2x²-8x-5
¦ définie sur [-2 ; 2 ] par -x²
+ 3x + 5
¦ définie sur [ -1 ; 3 ] par : ¦ (x) = x3 + x + 1
Exercice
n°4
Soit ¦ la fonction définie sur [0 ;
4 ] par ¦(x) = 2x²-10x+.3.
1°)
Déterminer la fonction dérivée ¦'.
2°)
Dresser le tableau de variation de ¦
3°)
En déduire que ¦ admet un minimum obtenu pour une valeur de x que l'on
précisera. Donner la valeur de ce minimum.
Exercice
n°5
On
considère la fonction ¦ définie sur l'ensemble des nombres réels par ¦(x) = (x+1)(2x-3)
1°)
En développant le produit (x+1)(2x-3), donner une autre expression de ¦.
2°)
Calculer ¦'(x)
Exercice
n°6
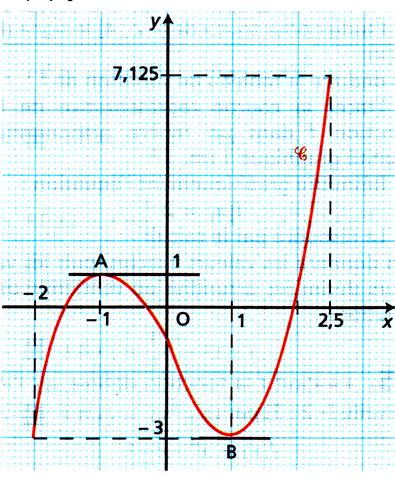 La courbe C est une courbe
représentative d'une fonction ¦ sur l'intervalle [ -2 ; 2,5 ]
La courbe C est une courbe
représentative d'une fonction ¦ sur l'intervalle [ -2 ; 2,5 ]
1°) A
partir d'observations graphiques :
a) Dresser le tableau de
variation s de ¦
b) Donner les valeurs approchées
des trois solutions de l'équation ¦(x) = 0.
2°)
Sachant que pour tout x de [ -2 ; 2,5], ¦(x) = x3 - 3x -1,
on se propose dans cette question de retrouver les variations de ¦ en utilisant la fonctions
dérivée ¦' de ¦.
a)
Calculer
¦'(x). vérifier que ¦'(x) = 3(x-1)(x+1)
b)
Reproduire
et compléter le tableau de signe suivant :
|
x
|
-2 -1 1 2,5
|
|
Signe de x-1
|
0
|
|
Signe de x+1
|
0
|
|
Signe de ¦'(x)
|
0 0
|
c)
En
déduire le tableau de variations de ¦
Exercice
n°7
On décide d'étudier pour une période donnée le
bénéfice d'un sous-rayon d'un magasin d'alimentation.
On désigne par b le bénéfice exprimé en € et
par x le chiffre d'affaires hors taxes (H.T.) exprimé en €.
Partie A
On suppose que le bénéfice est donné par la relation:
b(x) = 0,35x-45
1°) Pour quel chiffre d'affaires hors taxes, à l'€ près,
a-t-on un bénéfice nul ?
2°) Calculer le bénéfice maximal que l'on peut espérer
sachant que le chiffre d'affaires ne peut excéder 300 €.
3°) Soit f la fonction définie sur l'intervalle [150;
30~ par:
f(x) = 0,35x-45
Tracer la courbe représentative de f dans un repère
orthogonal.
Échelles:axe des abscisses:1 cm pour 20
€; axe des ordonnées:1 cm pour 5 €.
4°) Déterminer graphiquement à partir de quel chiffre
d'affaires on obtient un bénéfice supérieur ou égal à 20 €.
Partie B
On constate en fait que, pour la période donnée,
l'expression du bénéfice est plus proche de la relation :
b(x) = -0,005x² +2,5x+c
1°) Calculer c pour que le bénéfice reste de 60 € pour
un chiffre d'affaires de 300 €.
2°) Soit g la fonction définie sur l'intervalle [150;
300] par:
g(x) = -0,005x² +2,6x-270
On a ainsi : g(x)
= b(x)
a) Reproduire et compléter le tableau suivant, puis
construire la courbe représentative de la fonction g dans le repère
utilisé pour la partie A.
|
x
|
150
|
180
|
210
|
240
|
260
|
280
|
300
|
|
g(x)
|
7,5
|
36
|
|
66
|
68
|
|
60
|
b) Donner l'expression de la fonction dérivée g' de
la fonction g.
c) Résoudre l'équation g'(x) = O ; on note x0
sa solution.
d) On admet que pour un chiffre d'affaires hors taxes
égal à x0 le bénéfice est maximal. Calculer le bénéfice
maximal.
(D'après un sujet de Bac)


