@

warmaths

Pour Aide et Formation Individualisée

DOSSIER STATIQUES

ICI pour aller directement aux informations « cours »

INFORMATIONS PEDAGOGIQUES :

N°cours 2

Matière :SCIENCES

« TRAVAUX »

TITRE : STATIQUE : Etude d’un point matériel en équilibre sous l’action de deux et trois forces

Classe : collège-….

NIVEAU :Débutant

OBJECTIFS :

- Savoir :définir l’ Action- réaction

I ) Pré requis: (pour remédiation ou mise à niveau)

Pré requsi

MODULE : mécanique « généralités »

Tableau des unités de NEWTONS

Bi- point - ………

Somme de vecteurs.

II ) ENVIRONNEMENT du dossier :

Index

Dossier précédent :

Action et réaction.

Dossier suivant :

Info :

Liste des cours.

III ) INFORMATIONS « formation leçon » :

T est

COURS

Travaux auto - formation.

Corrigé des travaux auto - formation.

Contrôle

évaluation

INTERDISCIPLINARITE

Co r rigé Contrôle

Corrigé

évaluation

Chapitres :

Notion de force.

Principe de l’égalité de l’action et de la réaction.

Equilibre d’un point matériel :

IV ) DEVOIRS ( écrits):

Devoir diagnostique L tests.

Devoir Auto - formatif (intégré au cours)

Devoir Formatif « Contrôle : savoir » ; (remédiation)

Devoir Formatif « Evaluation savoir faire » (remédiation)

Devoir sommatif.

Devoir certificatif : (remédiation)

* remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour conclure une formation .

Leçon	Titre
N°	STATIQUE : étude d’un point matériel en équilibre sous l’action de deux et trois forces

	COURS
	I ) Notion de force.	La notion de force nous est donnée par nos efforts musculaires.
	FORCES DE CONTACT .
	« pousser »		« tirer »

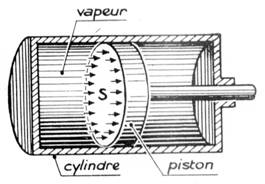
			Vapeur sur le piston
	Dessiner un exemple :
	FORCES A DISTANCE.
	L’attraction terrestre.		Le courant électrique déviant l’aiguille d’une boussole.


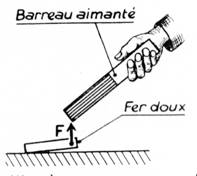
				L’aimant sur un morceau de fer.
	Dessiner un exemple :
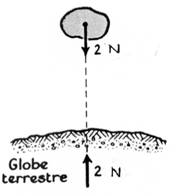
	Il faut savoir : On dit que deux forces sont directement opposées si elles ont la même droite d’action, la même intensité et de sens contraire.( les vecteurs qui les représentes sont directement opposés.
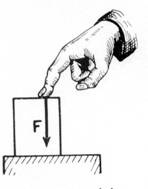
	Exemple : l’action de l’index sur l’anneau et la réaction de l’anneau sur l’anneau sont deux forces directement opposées.

	Remarque : l’action et la réaction sont des forces directement opposées qui agissent sur des corps différents.

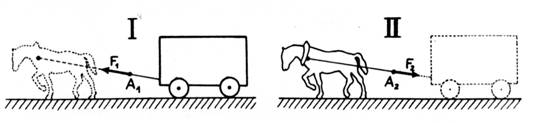
	Remarque : le cheval tire sur la voiture qu’il entraîne. Mais la voiture tire de sens contraire sur le cheval. L’action est la réaction s’exercent entre corps en mouvement comme entre corps au repos. Les forces et s’exercent en tout point « A » du trait. Juste avant le démarrage les forces et sont égales et directement opposées suivant le trait .
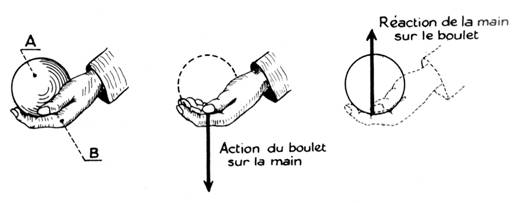
9@	II ) Principe de l’égalité de l’action et de la réaction. Une force appliquée à un corps « A » est toujours due à l’action d’un autre corps « B » qui agit, soit au contact, soit à distance. La main et le boulet sont seuls visibles. On sait malgré cela que le boulet exerce sur la main une « action » et la main exerce sur le boulet une « réaction ». PRINCIPE DE « NEWTON » ( Newton :savant anglais 1642-1727) Si un corps « A » exerce une force (ACTION) sur un corps « B », inversement « B » exerce sur « A » une force directement opposée ( REACTION). Cet énoncé ne suppose pas que les corps « A » et « B » soient au contact ; il s’applique aussi lorsqu’ils agissent l’un sur l’autre à distance. Le principe de l’égalité de l’action et de la réaction s’applique , que les corps soient en repos ou en mouvement.


	Ainsi les forces vont toujours de paires : pas d’action sans réaction, c’est à dire pas de force sans force directement opposée. Mais « action » et « réaction » sont appliquées sur des corps différents, en contact ou non, en repos ou en mouvement.
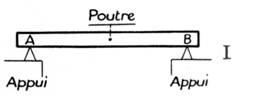
	Applications du principe d’égalité de l’action et de la réaction : Soit 2 exemples simples : 1° exemple : Réactions aux appuis d’une poutre : Soit une poutre de poids « P » donc attirée vers le bas, reposant sur deux appuis « A » et « B » . Pour simplifier l’étude, nous supposons que ces appuis sont des arêtes de deux prismes triangulaires :
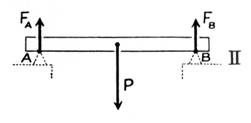
	La poutre exerce sur chacun d’eux une poussée verticale, sens de haut en bas.
	Inversement, chaque appui réagit sur la poutre avec une force verticale, sens de bas en haut.
	La poutre se trouve donc soumise aux forces suivantes, supposées dans un même plan :
	a) Forces de contact exercées par les corps qui la touchent : en A , en B , appelées « réactions des appuis ». b) Forces à distance exercées par les corps qui l’attirent : appliquée au centre de gravité « G » de la poutre.
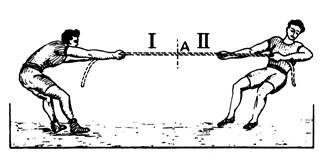
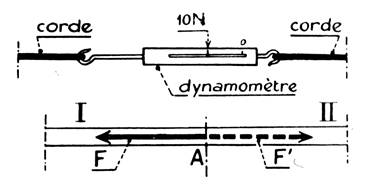
	2^ème exemple ) Force de tension d’une corde : (tir à la corde ou remonté d’un seau d’eau du fond d’un puit), cette force s’exerce en une section droite de cette corde. Si la corde était coupée en cette section, il faudrait, pour maintenir chaque tronçon dans le même état qu’avant la coupure, appliquer une force sur chaque bout de la coupure. Remarque : la partie I de la corde tire sur la partie II avec une force « F = 10 N» et inversement la partie II tire sur la partie I avec une force « F’ = 10N » . Les forces sont directement opposées en vertu du principe d’égalité de l’action et la réaction. La valeur commune de ces deux forces mesure « la force de tension » de la corde dans la section considérée. Si une corde en équilibre est parfaitement flexible et de poids négligeable, la force de tension a la même valeur dans toutes les sections ; elle a même intensité que la force qui tire à l’ un des bouts de la corde .
	9@ INFO plus ( expériences)
	III ) Equilibre d’un point matériel :sous l’action de trois forces.(et plus)
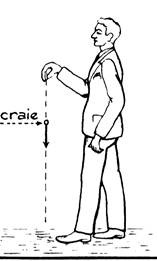
	Un point matériel soumis à l’action d’une seule force , son poids par exemple, ne reste pas en équilibre. Exemple : on lâche un morceau de craie , « il tombe », donc il n’est pas en équilibre. Or à partir du moment où on le lâche, une seule force agit sur lui : son poids, qui est une force verticale, de sens de haut vers le bas*.
	Remarque : Le morceau de craie, à partir du moment où on le lâche, n’est plus en contact qu’avec l’air et les forces qui résultent de ce contact (poussée hydrostatique et résistance de l’air) sont pratiquement négligeables)				* Le morceau de craie finit par s’arrêter sur le sol, où il reste immobile. Mais il est alors soumis à deux forces : son poids et le réaction du sol.
	Définition 1 : « points matériel » : il nous arrive, au cours de nos expériences, de faire agir des forces sur des corps solides de petites dimensions, donc de « poids négligeable » par rapport à ces forces. Dans les schémas nous représentons ces solides par des points et nous les appelons : points matériels.
	Définition 2 : « équilibre » : En mécanique , on emploie souvent le mot « équilibre ». pour en comprendre le sens on dit en statique que : un corps est en équilibre lorsqu’il est au repos, c’est à dire immobile.
	A) Point matériel soumis à l’action de deux forces :
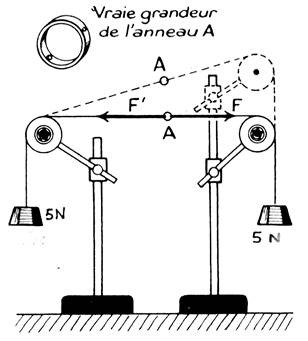
	Conditions d’équilibre : les deux conditions nécessaires et suffisantes pour qu’un point matériel soit en équilibre sous l’action de deux forces est que celles -ci soient de même intensité et directement opposées.
	Voir description de l’ expérience : info plus.
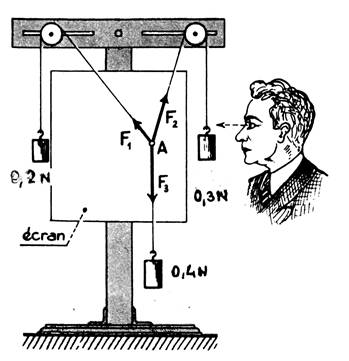
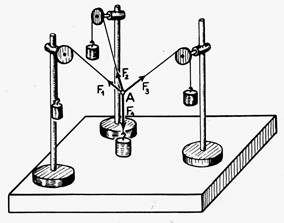
	B) Point matériel soumis à l’action de trois forces : Conditions d’équilibre : - La situation d’équilibre de trois forces d’intensités données est « unique ».(à voir : au début des expériences :si l’on fait varier l’intensité d’une des trois forces il y a recherche d’équilibre du système,, ensuit celui ci se stabilise) -La situation d’équilibre est obtenue lorsque les trois forces sont concourantes en un point et qu’elles sont dans un même plan.

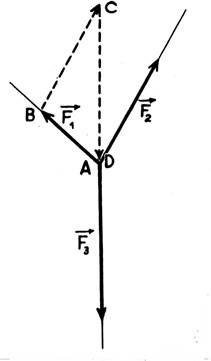
	La situation d’équilibre est montrée par le tracé : ( info : 9tracé) Le bi- point : (B,C) représente le vecteur : Le bi- point : (A,B) représente le vecteur : Le bipoint : (C,D) représente le vecteur : Il suffit de tracer « la somme géométrique » des trois vecteurs -forces. Géométriquement : On obtient un polygone à trois forces, il est ou « ouvert » ou « fermé »: - s’il est « ouvert » : il n’y a pas de situation d’équilibre.(il faudrait une autre force coplanaire pour fermer le polygone) ; le vecteur « somme » n’ est pas égal à « zéro ». le système n’est pas en équilibre. - s’il est « fermé » : il y a situation d’équilibre , le vecteur « somme » est égal à « zéro »
	On retiendra : Pour montrer qu’un point matériel est en équilibre sous l’action de trois forces , il faut et il suffit de montrer que la somme géométrique des trois vecteurs forces soit nulle.
	B) Point matériel soumis à l’action d’ un nombre supérieur à trois forces : Pour obtenir la condition d’équilibre on peut rencontrer deux cas : les forces sont situées dans un même plan , ou les forces ne sont pas dans un même plan. 1° Si elles sont dans un même plan, on procédera exactement comme il ; vient d’être dit pour trois forces. On constatera encore que la « somme géométrique » des vecteurs qui les représentent est nulle.

	2°)Si elles ne sont pas dans un même plan, il est impossible d’effectuer un tracé dans l’espace. C’est une situation complexe : il a faut travailler sur les projections sur trois plans perpendiculaires et vérifier plan par plan que les vecteurs sommes qui sont « assimilables » à un point converge en un et même point. (cette étude fait intervenir des connaissances supérieures au niveau IV)
	On énoncera seulement le théorème suivant : la condition nécessaire et suffisante pour qu’un point matériel soit en équilibre est que la somme géométrique des vecteurs représentant les forces qui le sollicitent soit nulle.

	Problèmes d’ Application
	Problème 1
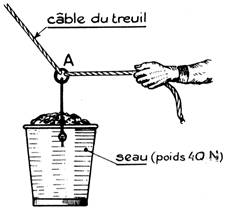
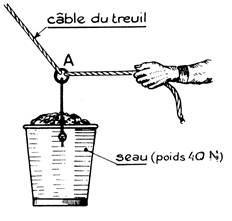
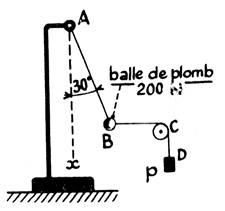
	Un seau plein de terre pèse 40 N. Il est suspendu au câble d’un treuil par l’intermédiaire d’un anneau qu’un ouvrier tire horizontalement à l’aide d’une corde. La force exercée par l’ouvrier est de 30 N. L’équilibre étant réalisé, déterminer la tension du câble et sa direction ( « α » est l’angle que fait le câble avec la verticale.
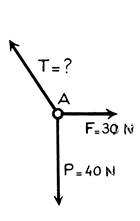
	L’équilibre étant réalisé , les forces qui agissent sur l’anneau (assimilé à un point matériel) sont : - la force de contact exercée par l’anse du seau : force verticale, sens,de haut en bas, intensité égale au poids du seau : P = 40 N . - la force de contact « F »exercée par la corde tirée par l’ouvrier dont l’intensité est de 30 N. - La force de contact « T » exercée par le câble : « inconnue »
	Puisqu ‘il y a équilibre , ces trois forces sont dans un même plan et l’on peut écrire que : + + = (1)
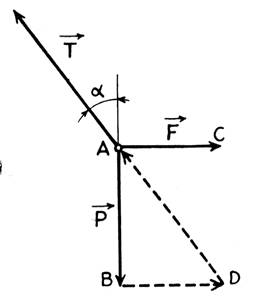
	Les forces « F » et « P » sont connues. Nous traçons les vecteurs correspondants (échelle : 1 cm = 1 N) soient : (A,B) = = (B,D) = = Dans l’addition des vecteurs : est équipollent à est équipollent à Pour conclure à la situation d’équilibre, il nous reste à tracer pour fermer le polygone (triangulaire).
	Nous avons : + + = ou + + = (2) Nous comparons : ( 1) et (2) , nous en tirons : = Le vecteur est donc équipollent à , ce qui nous donne sa direction et sa grandeur. 1°) mesurons DA : DA = 2,5 cm donc = 2 ´ 2,5 = 5 N 2°) Mesurons l’angle α avec un rapporteur : α = 37 °
	Problème N°2
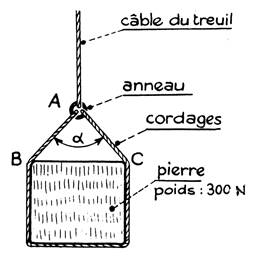
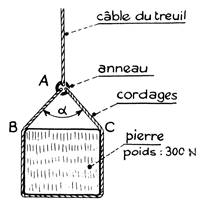
	Un maçon soulève une pierre pesant 300 N à l’aide de cordages tous attachés au même anneau. On demande de déterminer graphiquement les forces de tension dans les brins AB et AC. Montrer qu’en pratique l’angle alpha « α » ne doit pas être trop grand (pour simplifier l’ étude on admettra que tous les cordages sont dans le même plan.) On demande quelles sont les tensions du câble et des cordages AB et AC ?
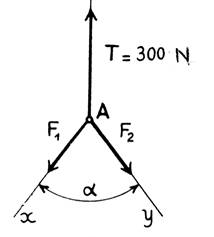
	Nous considérerons l’anneau « A ». Il est en équilibre sous l’action des forces de contact suivantes : 1°) la traction verticale du câble qui s’enroule sur le tambour d’un treuil : = 300 N. 2°) la traction oblique du tronçon AB de la corde. 3°) La traction oblique du tronçon AC.
	Ces trois forces sont en équilibre et l’on peut écrire : + + = Nous connaissons T en direction, sens et grandeur , et seulement les direction « A x » et Ay » des deux autres forces. Nous pouvons les déterminer comme suit :
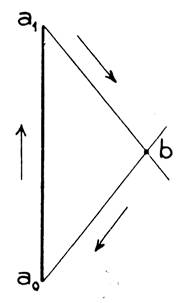
	Traçons le vecteur a₀ a₁ représentant la force « » (échelle 1mm= 10 N) par a₁ , menons la parallèle à « ay » et par a₀ la parallèle à « A x » coupant la précédente en « b » . les vecteurs et et ont une somme géométrique nulle. Le vecteur représente la force et le vecteur la force . Mesurons : a₁b = 20 mm ba₀ = 20 mm Par suite et = 200 N ou 20 daN
	Conclusion : Si les brins AB et AC tirent sur l’anneau avec des forces et inversement l’anneau tire sur les brins avec des forces directement opposées. Les forces de tension dans les deux brins sont donc égales à 200 N ou 20 daN Vous vérifiez que , plus l’angle α est grand , plus les segments a₁b et ba₀ sont longs, donc plus les brins sont tendus ; si les forces de tension sont trop élevées , la corde risque de se rompre.
	A méditer si vous voulez remorquer ; tracter ; …..ou lever de fortes charges. Observez autour de vous des situations.

Leçon	Etude d’un point matériel en équilibre sous l’action de deux et trois forces
	TRAVAUX d ’ AUTO - FORMATION




	TRAVAUX d ’ AUTO - FORMATION : CONTROLE

		1°) On dit que deux forces sont directement opposées:si ?......
		2°) Pour montrer qu’un point matériel est en équilibre sous l’action de trois forces que faut-il ?
		3°) Quelle est la condition nécessaire et suffisante pour qu’un point matériel soit en équilibre ?
		TRAVAUX d ‘ AUTO - FORMATION EVALUATION
		A ) Un seau plein de terre pèse 40 N. Il est suspendu au câble d’un treuil par l’intermédiaire d’un anneau qu’un ouvrier tire horizontalement à l’aide d’une corde. La force exercée par l’ouvrier est de 30 N. L’équilibre étant réalisé, déterminer la tension du câble et sa direction ( « α » est l’angle que fait le câble avec la verticale. (corrigé dans le cours)
		B) Un maçon soulève une pierre pesant 300 N à l’aide de cordages tous attachés au même anneau. On demande de déterminer graphiquement les forces de tension dans les brins AB et AC. Montrer qu’en pratique l’angle alpha « α » ne doit pas être trop grand (pour simplifier l’ étude on admettra que tous les cordages sont dans le même plan.) On demande quelles sont les tensions du câble et des cordages AB et AC ? (corrigé dans le cours)
		C) tracer le polygone des forces. (corrigé dans le cours)
		D) Une balle en plomb pesant 200 N est suspendue à un fil AB. Elle est tirée horizontalement par un fil BC tendu par un poids P .Lorsque le système est en équilibre, AB fait avec la verticale Ax un angle de 30°. Déterminer graphiquement et par le calcul la force de tension des fils AB et BC , et en déduire le poids de la charge accrochée en D. (échelle des forces : 2 mm pour 10 N)
		E ) Un anneau « A » qu’on assimile à un point est attaché à trois câbles tendus par des ressorts. L’un de ces ressorts est étalonné (dynamomètre) ?. Lorsque le système est en équilibre, le dynamomètre indique une force de tension de 230N et les câbles forme entre eux les angles indiqués sur la figure. Déterminer graphiquement les forces de tension dans les câbles AB et AC . (échelle des forces : 2 mm pour 10 N)

TRAVAUX N° d ’ AUTO - FORMATION : CONTROLE CORRIGE
	1°) On dit que deux forces sont directement opposées : Si elles ont la même droite d’action, la même intensité et de sens contraire.( les vecteurs qui les représentes sont directement opposés.
	2°) Pour montrer qu’un point matériel est en équilibre sous l’action de trois forces , il faut et il suffit de montrer que la somme géométrique des trois vecteurs forces soit nulle.
	3°) la condition nécessaire et suffisante pour qu’un point matériel soit en équilibre est que la somme géométrique des vecteurs représentant les forces qui le sollicitent soit nulle.