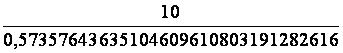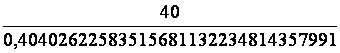Mathématiques :
(devoir donné à
Wassigny 02)
Le 12 novembre
2010
|
|
Problèmes : |
|
|
|
|
|
|
|
Exercice
1 |
|
|
|
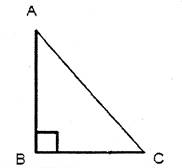
a) On a l’angle ACB = 35° et AB = 10 cm .
Calculer AC ( au centième ) |
|
|
|
|
|
|
|
Remarque :
AB est le côté opposé à l’angle ACB ; AC est l’hypoténuse du triangle ACB. La relation trigonométrique
faisant intervenir le côté opposé à un angle et l’hypoténuse est le sinus. Tel que Inventaire des
données : Sinus 35° = 0,57357643635104609610803191282616 AB = 10 AC = x On remplace dans
l’égalité : On
transforme : x
= X =
17,434467956210980198376834167244 Soit AC
= 17,43 à 0,01
|
|
|
|
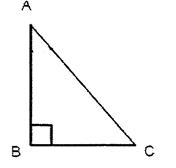
On a : AC = 45 cm et
BC = 27 cm . Calculer la valeur de l’angle CA B (au
degré) |
|
|
|
|
|
|
|
Si l’on considère l’angle CAB ; AC est l’hypoténuse et BC est le côté opposé à cet angle. Avec ces données nous pouvons calculer la valeur du sinus de
l’angle CAB : Sin CAB = 0,6 Avec la calculatrice nous pouvons obtenir la valeur de l’angle : Calculatrice : taper : « 0,6 » ; « inv. » ; « sin » ; »= » :
Affichage écran : 36,869897645844021296855612559093° Soit : Sin-1 CAB =
36,869897645844021296855612559093° soit l’angle , au
degré prés, mesure 37° |
|
|
|
|
|
|
|
Exercice 2 |
|
|
|
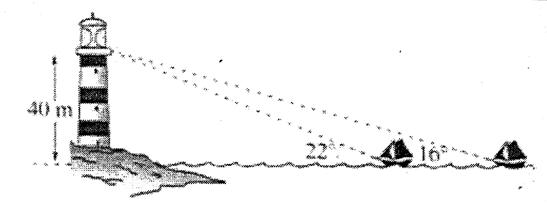
Hauteur à considérer :
40 m , le bateau le plus prés du phare mesure avec
son sextant un angle de 22° et la bateau le plus éloigné qu phare
mesure un angle de 16°. |
|
|
|
Questions : 1°) A quelle distance ,du phare, se trouve les deux bateaux. ? Autre
façon de poser la question : calculer la distance entre chaque bateau et la côte. On désigne B1 le
bateau le plus prés et B2 le bateau le plus éloigné de la côte. Calcul de la distance
que sépare B1 du phare.( dB1) ( Triangle
rectangle , avec un angle et une distance comme donnés on applique une relation
trigo .) : On applique la tangente : ( 40 / dB1) =
tan.22° Recherche de la
valeur décimale de tan. 22° : = 0,40402622583515681132234814357991 On pose : ( Produit en croix = 40 fois
1 = dB1 fois 0,40402622583515681132234814357991) ·
dB1 = ·
dB1 = 99,00347413665183300960052984327 ·
conclusion : dB1 =
99 m A vérifier en construisant le plan
à l’échelle. …… Calcul de la distance
que sépare B2 du phare.( dB2) ( Triangle
rectangle , avec un angle et une distance comme donnés on applique une relation
trigo .) : On applique la tangente : ( 40 / dB2) =
tan.16° Recherche de la
valeur décimale de tan. 16° : = 0,28674538575880794004275806273267 ( 2°) En déduire la distance
séparant chaque bateau . distance séparant les deux
bateaux : dB1 - dB2 = ….. |
|
|
|
|
|
|
|
Exercice 3 |
|
|
|
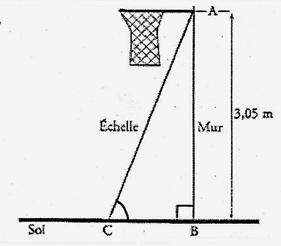
1° Paul veut installer chez
lui un panier de basket .Il doit le fixer à 3,05 m du sol. L’échelle dont il
se sert mesure 3,20 m de long. A quel distance du pied du mur doit-il placer
l’échelle pour que son sommet soit juste au niveau du panier ? (Donner
une valeur approchée au cm prés.) 2°) Calculer l’angle formé
par l’échelle et le sol. ( Donner une valeur approchée au degré prés.) |
|
|
|
|
|
|
|
Exercice 4 |
|
|
|
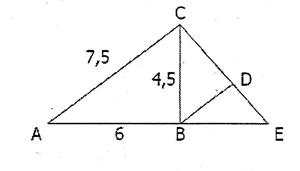
On donne AB = 6 cm ;
AC = 7,5 cm ; BC = 4,5 cm E est le point de [ AB) tel
que AE = 10 cm . 1°) Démontrer que le
triangle ABC est rectangle en B. 2°) a) Calculer BE b) Calculer BCE (
arrondir au degré) 3°) La parallèle à (AC)
passant par B coupe (CE) en D. Calculer BD |
|
|
|
|
|
|
|
Exercice 5 |
|
|
|
Calculer cos (x) lorsque
sin (x) = 0,4 Arrondir aux dixièmes
.. ( ? prés..) |
|
|
|
|
|
|
|
|
|
|
|
|
|