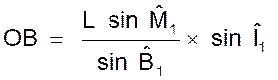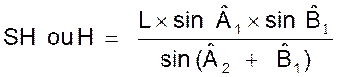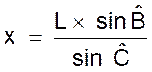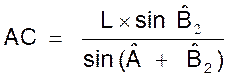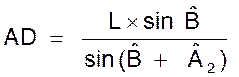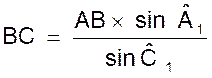|
|
|
||||||||
|
|
|||||||||
|
|
APPLICATIONS :
situations problèmes avec LES RELATIONS TRIGONOMETRIQUES
. |
|
|||||||
|
|
|
||||||||
|
|
Champ
d’application - levée de plan et arpentage |
|
|||||||
|
|
Ce
document vous montre des applications des relations trigonométriques. Et des
problèmes à résoudre………… ! NOTA :
Traiter
les problèmes en utilisant les tables
à 3 décimales ; à 5 décimales
et comparer les résultats obtenus avec ceux fournis par l’emploi de la
calculatrice. Pour chaque cas placer ces 3 résultats dans un tableau. |
|
|||||||
|
|
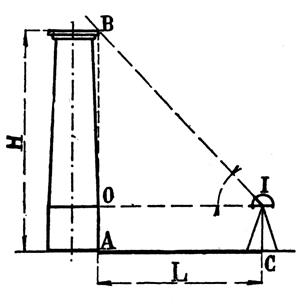
1°)
Hauteur d’une tour , d’une cheminée dont le pied
est accessible. |
|
|||||||
|
|
Formule :
|
|
|
||||||
|
PB
1 : Calculer
H : Si L = 32
m , l’angle I = 42°35’ si le point I se trouve (graphomètre)
à pour hauteur 1,15 m. ( 30,56 m par excès) |
|||||||||
|
|
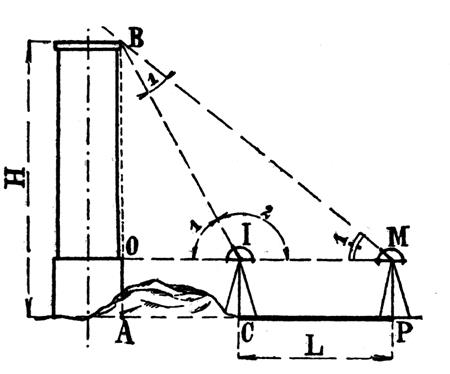
2°)°) Hauteur d’une tour , d’une cheminée dont le pied est
inaccessible. |
|
|||||||
|
|
Formule :
H = AB = OB + hauteur du graphomètre. |
|
|
||||||
|
PB 2 : Calculer H : Si L = 27
m , l’angle M1 = 32°15’ et l’angle I1 = 48°32’. |
|||||||||
|
PB 3 : Trouver la hauteur d’une
tour à pied inaccessible, sachant que les mesures nécessaires ont donné : Si L =
38 m ,
l’angle M1 = 28° 45’ et l’angle
I1 = 43° 54’. |
|||||||||
|
|
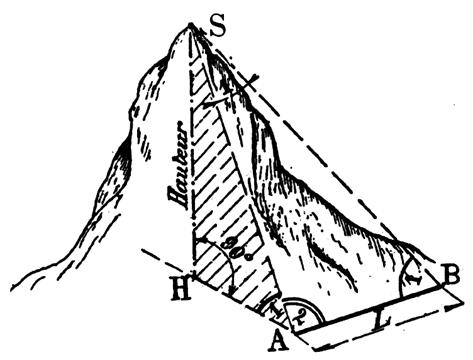
3°)
Hauteur d’une montagne à pic sur une plaine. |
|
|||||||
|
|
Formule :
|
|
|
||||||
|
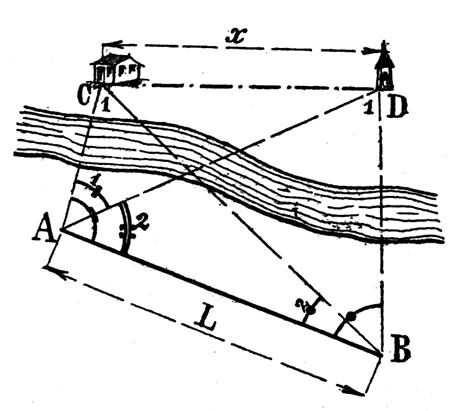
PB 4 : Trouver
la hauteur d’une montagne sachant que : L =
2 438 mètres , l’angle A1 = 24° 15’ , l’angle B1
= 40° 12’ et l’angle A2 =
34° 25’ |
|||||||||
|
|
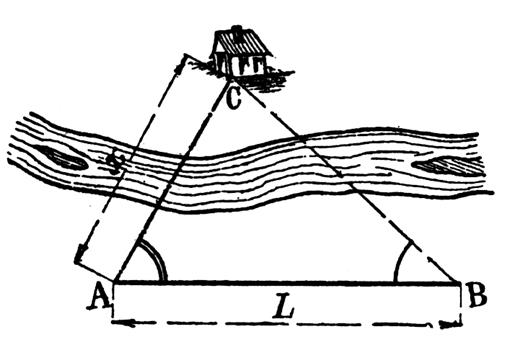
4°)
Mesurer la distance de deux points dont un seul est accessible et l’autre
visible. |
|
|||||||
|
|
On
cherche AC. On
jalonne et l’on mesure une base d’opérations AB = L On mesure
ensuite les angles A et B. Formule :
|
|
|
||||||
|
PB
5 : Trouver
la distance de deux points A et C , le dernier
inaccessible sachant que : L = 1 845 mètres ; l’angle A = 72° 35 ‘ et
l’angle B = 45°15’ |
|||||||||
|
|
5°)
Mesurer la distance de deux points
inaccessibles. |
|
|||||||
|
|
CD = ? Formule : L’angle A = l’angle A1 + l’angle A2 L’angle B = l’angle B1 + l’angle B2
AD et AC
étant connus ainsi que l’angle A , on a dans le triangle CAD : |
|
|
||||||
|
|
(CD)² ou x² = (AC)²
+ (AD)² - 2(AC) (AD) cos |
|
|||||||
|
PB 6 : Trouver
la distance de deux points inaccessible
C et D connaissant les mesures
nécessaires : AB = 2 140 mètres , l’angle A = 72° 15’ , l’angle A1
= 39° 55’ ; l’angle A2 = 31° 56’ L’angle B2 = 24° 48 ‘ et l’angle B = 63° 25’ |
|||||||||
|
|
6°)
Prolonger un alignement au delà d’un obstacle .(une
montage , une mare , une étang,….) |
|
|||||||
|
|
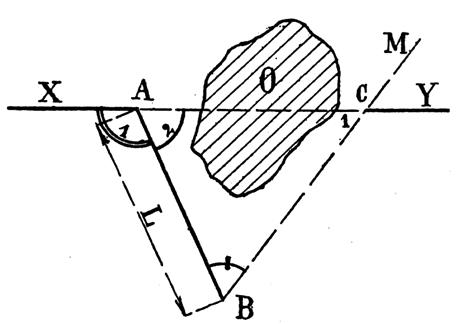
On veut
prolonger XA au delà de l’obstacle O
suivant CY. On se
place en B permettant d’apercevoir les deux régions de part et d’autre de
l’obstacle et on jalonne les deux alignement BA et BM .
ON mesure la distance AB ainsi que
l’angle A 1 et l’angle B. On
applique la relation des sinus (BC) / (sin A 2 )= (AB) / (sin C1
) mais sin
A2 = sin A1 ; (angles supplémentaires) |
|
|
||||||
|
|
D’où : (BC) /
(sin A1 )= (AB) / (sin C1 ) On
obtient la formule : La
longueur BC étant calculée , on la porte sur
l’alignement BM et l’on trace ensuite l’alignement CY faisant avec BC
l’angle BCY = 180° - |
|
|||||||
|
PB
7 : Traiter
le problème du prolongement au delà d’un obstacle ,
sachant que les mesures ont donné : AB =
1 835 mètres ; l’angle A1 = 112° 48’
et l’angle B = 54° 23’ |
|||||||||
|
NOTA :
Traiter
les problèmes en utilisant les tables
à 3 décimales ; à 5 décimales
et comparer les résultats obtenus avec ceux fournis par l’emploi de la
calculatrice. Pour chaque cas placer ces 3 résultats dans un tableau. |
|||||||||