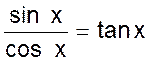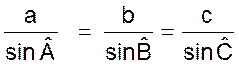|
|
TRAVAUX
sur LES RELATIONS TRIGONOMETRIQUES
. A) Exercices. B)
Problèmes approches théoriques et de « à démontrer ». |
|
|||
|
|
Pour
vous entraîner - Pas de corrigé
disponible. |
|
|||
|
|
|
||||
|
1 |
Vérifier les relations sin² + cos2 x =
1 et
|
|
|||
|
2 |
Trouver le cosinus et la tangente d’un angle aigu
dont le sinus vaut ( 1/3) |
|
|||
|
3 |
Trouver le sinus et la tangente d’un angle aigu dont le cosinus est
(2/5 ) |
|
|||
|
4 |
Résoudre un triangle ABC rectangle en A connaissant
|
|
|||
|
|
a) a = =
15 ; B = 27° |
c)
a = = 17 ; B = 27 gr |
|
||
|
b) a = =
23,5 ; b = 12,75 |
d)
a = = 75 ; B = 47,5 (B et C en
degré et grade) |
||||
|
5 |
Construire les solutions des équations
suivantes : |
|
|||
|
|
a) 10sin x — 3 = 0 |
b) 5
sin x -.4
= 0 |
c) 7
sin x - 3 = 0 |
|
|
|
d) 7cos
x - 3 = 0 |
e) cos x - 0,43
= 0 |
f) 8cosx - 5 = 0. |
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
B) PROBLEMES approches Théoriques et de « à démontrer » |
|
|||
|
6 |
Soit un triangle ABC rectangle en A et de hauteur AH. Soit BC = a
et « x » la mesure de l’angle B en degrés.
Évaluer, en fonction de « a » et des rapports trigonométriques de
l’angle « x » les longueurs
des segments suivants AB, AC, AH, BH et CH. |
|
|||
|
7 |
Soit un triangle ABC rectangle en A et tel que AC
= 2 AB. Déterminer les angles de ce triangle. |
|
|||
|
8 |
Soit un triangle isocèle ABC de base BC et AH la hauteur issue de A.
Soit BAC = 2x et AD = a. 1°) Évaluer en fonction de a et des rapports trigonométriques de
l’angle x les longueurs (les segments AH et BH. 2°) Évaluer en fonction de a et des rapports trigonométriques de
l’angle 2 x la hauteur issue de B. Application: a = 15 cm ; x = 15° |
|
|||
|
9 |
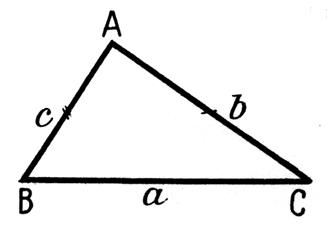
Soit un triangle ABC de côtés a, b et c et dont les
angles sont aigus. Soit O le centre du cercle circonscrit et H le milieu de
DC. 1° Que peut-on dire du triangle BOH ? Évaluer le rayon du cercle
circonscrit eu fonction de a et d’un rapport trigonométrique de
l’angle A. 2°) Démontrer
la relation : |
|
|||
|
10 |
On donne un triangle ABC rectangle en A dans lequel l’angle C 30° et l’hypoténuse DC = a. 1°) On mène la hauteur AH. Calculer AH, BH et CH, en fonction de a. 2°) On trace la bissectrice AD
de l’angle A et l’on abaisse les perpendiculaires DE et DF sur AD et AC.
Comparer les triangles DFC, BED et ABC. Calculer BD et DC. 3°) Déterminer la nature du quadrilatère AFDE.
Calculer son côté AE et sa diagonale AD.. |
|
|||
|
11 |
Deux droites perpendiculaires z’ z et y’y se
coupent en O. On porte sur O x une longueur OA et sur O y une longueur OB
telles que OA = OB = a. Une demi-droite A z coupe O y en un point C
situé entre O et B et la perpendiculaire DI abaissée de B sur A z coupe Or’
en D. 1°) Démontrer que OC = OD. 2°) Montrer que le quadrilatère
OCID est inscriptible et que 10 est bissectrice de l’angle CID. 3°) Dans
le cas où l’angle OAC = 30° , calculer
en fonction de « a » les
longueurs AC, OC, AD et le rayon du cercle circonscrit au quadrilatère OCID. |
|
|||
|
12 |
Soit un triangle ABC, tel que BC = 1°) Montrer que les quatre points B, F, E, C sont sur un même cercle. Préciser
l’a position de son centre I. Quelle est la position du point E sur le
cercle? 2°) Montrer que le triangle IFE
est équilatéral. 3°) Calculer en fonction de a
la longueur des segments CE et BE. En utilisant le triangle AEB, calculer ensuite AD, puis AE. 4°) Soit K l’intersection de IF
avec BE. Montrer que les triangles IBK et CEE sont semblables. |
|
|||
|
|
C)
Problèmes en rapport avec des FIGURES GEOMETRIQUES |
|
|||
|
13 |
Dans un trapèze isocèle ABCD la grande base AD mesure |
|
|||
|
14 |
Dans un trapèze rectangle ABCD dont les bases sont AB et CD et dont BC
est le côté oblique on donne AB = |
|
|||
|
15 |
Dans un cercle de centre O et de diamètre DC = 1°) On demande de calculer le cosinus,
le sinus et la tangente de l’angle ARC. 2°) On mène la hauteur AH du
triangle BAC; calculer AH de deux façons a) en utilisant un des résultats trouvés précédemment; b) en appliquant un théorème relatif aux triangles rectangles. 3°) On trace la médiane BM,
dont le prolongement coupe le cercle (O) en D . Calculer BM et MD. 4°)
Comparer les triangles MDC et MAD. En déduire la longueur de la corde
AD. |
|
|||
|
16 |
Soit un triangle rectangle ABC, d’hypoténuse DC = a et de ctés
CA = b. et AD = c. 1° ) Construire les cercles S 1
de diamètre BC, S2 de
diamètre CA et S3 de diamètre AH. Où se coupent S1 et S2?
S2 et S3? 2°) Une droite D passe par A
sans traverser le triangle ABC et recoupe S1 en E, S2 en F et S3 en G. Montrer que les trois triangles AFC,
BGA, BEC sont semblables . 3°) On
désigne par a l’angle aigu CAF. Calculer en
utilisant « a », « b », « c »et les
rapports trigonométriques sin a et cos a les côtés de ces trois triangles et
vérifier la relation : EB.EC =
FC.FA + GA.GB. |
|
|||
|
17 |
Soient un triangle ABC rectangle en A, et D un point pris sur AC. On
mène la hauteur AH du triangle ABC et la perpendiculaire CE à la droite BD.
Les (Droites BA et CE se coupent en F. 1°) Comparer les triangles ABD et ECD. 2°) Démontrer que le quadrilatère ABCE est inscriptible dans un cercle
dont on déterminera le centre O. 3°) En supposant l’angle ABC = 60°, BC = 4°) Nature
des triangles ACF et BEF? Calculer les longueurs FA, FB et F’C. |
|
|||
|
18 |
Soit un trapèze ABCD, dont les angles A et D sont droits et dans
lequel la diagonale AC est perpendiculaire au côté DC. 1°) Montrer que les triangles ABC et CAD sont semblables. En déduire
la relation AC2 = AB . CD. 2°) On trace le cercle de
diamètre DC qui coupe AD en E. Quelle est la nature du quadrilatère AECD ?
Peut-on retrouver la relation établie précédemment? Que représente la droite
AC pour le cercle? 3°)
Sachant que AD = |
|
|||
|
19 |
Soient une droite xy et un point A dont la distance à zy est
AH = 1°) Calculer les longueurs des
segments AD, AE, AC. 2 °) Montrer que les triangles
ABC et AED sont semblables. Calculer la valeur du rapport de similitude et la
longueur du segment DE. 3°) Soit F
le point diamétralement opposé à D. Quelle est en degrés, la mesure de
l’angle DFE? Calculer la valeur du sinus de 75°. |
|
|||
|
20 |
On donne un carré ABCD de côté a. Sur CD on construit le triangle
équilatéral SCD, intérieur au carré. 1°) La médiatrice de AD coupe
AD en M et CD en H. Exprimer 5H et SM en fonction de a. Quelle est la
valeur de l’angle SAM? Calculer tan
SAM. 2°) Construire le centre O du cercle (ASB). Quelle est la nature du
quadrilatère OADS? Comparer le rayon du cercle O et le côté du carré AD DC. 3°) Montrer que les triangles
ASB et OSD sont semblables. Établir la relation AS .OD = a ² |
|
|||
|
21 |
Dans un triangle ABC, le côté BC est égal à « 2 a » et la
médiane AM à « a ». On trace la hauteur AD et l’on pose AMB = 2 x. 1°) Quelle est la nature du triangle ABC? Calculer AD et AC en
fonction de « a » et « x » . 2°) Calculer BD dans le
triangle ABD et DC dans le triangle ADC; en déduire que sin ² x + cos² x = 1. 3°) Dans le cas où x =
30°, achever les calculs relatifs à AD, AC, BD et DC. 4°) Soit MH la hauteur du
triangle AMC. Démontrer la similitude des triangles ADI) et AHM. En fonction
de a et de x , calculer AD dans le triangle AMD; démontrer que
le rapport de similitude des deux triangles précédents peut être évalué en
fonction de l’une des lignes trigonométriques de l’angle z. En déduire la valeur de ce rapport de similitude dans le cas où x =
60°. |
|
|||
|
|
D) SITUATIONS PROBLEMES INTERDISCIPLINAIRES |
|
|||
|
22 |
Soit un arbre matérialisé par un segment AD perpendiculaire en B à une
horizontale x y. On se place en un point C de xy tel
que BC = |
|
|||
|
23 |
Un bâton planté verticalement sur un sol horizontal dépasse la surface
du sol de |
|
|||
|
|
|
|
|||
|
|
|
||||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||