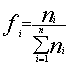I )  Notion  "d’effectif" et de "fréquence" :

Soit les deux tableaux :  sont -ils différents si oui par quoi sont -ils différents ?

1°) Que désigne  « x_i » ? :

2°) Que désigne  « n_i » ? 

3°)Traduire     : 

4°) Compléter les phrases suivantes :

Considérons la série statistique qui représente 500 automobiles classées dans un parc d’après leur marque . L’unité statistique est ici ……………….. , le caractère  (ou la variable)  qualitative est ……………………………….. . Un état de la variable ou une valeur de la variable est le « nom de la marque » : « Renault , Peugeot … » .L’effectif d’une marque « n_i » d’automobiles ayant cette

marque . Ainsi , l’effectif des voitures de marque Renault est 18O . L’effectif total de la population est ………….( ?)

        La deuxième colonne d’un tableau  statistique  enregistre   le nombre de fois que la valeur de la variable, mentionnée dans la première  colonne , a été  rencontrée , c’est la colonne des ………………?...................

 5°) Donner une définition de :

a) l’effectif :.

b) La fréquence :

c) Comment est noté  ce rapport ?

6°) Traduire la formule ci -contre :

que désigne « fi » ; « ni » et «  »

7°) compléter la phrase :

a)  La fréquence , n’a pas ………… , elle est exprimée en « ………….. » . Multipliée par 100  , elle s’exprime en  « ……………………».

b) dans le tableau  ci dessous on a calculé l’effectif total , la fréquence par « caractère » et on a exprimé chaque fréquence en pourcentage.

On remarquera que  pour un effectif total des caractères  : la somme des fréquences est égale à « 1 » et que la somme des pourcentages est égale à ………………. %.

II  )   L’ EFFECTIF : (simple et total)

8°) Que désigne l’Effectif simple ?  ( noté :………_i )   : (cette valeur est ………….)

 9°) Que désigne l’ Effectif total ? : ( noté ? )     (cette valeur est ……………..)

Nombre d’enfants

x _i

Effectif

n_i

Calculer l’effectif total :

0

 8

1

35

2

39

3

15

4

  4

5 et +

  1

N=

?= ………..

Exemple 2 :

   On donne dans le tableau un effectif par classe   (Tableau concernant une variable continue).

10)  Compléter les phrases suivantes :

· L'  effectif par « classe »  est un "sous- effectif" on le note  petit  " n " avec un ………………………………..

· On calculera  L' effectif total est la ……………………. qui sont inventoriés . « nombre d’entreprises » 

Distribution  du chiffre d’affaires  ( C. A.)  déclaré  par les entreprises de distribution d’une chaîne de magasin.

C.A.   .(milliers d’euros )

                  x _i

Effectifs

(  n _i )

L’effectif total est égal à la somme :

22 + 25 + 90 + 33  +24 + 6  = 200

N = 200

300 à moins  500

22

500 à moins  800

25

800 à moins  1 000

90

1 000 à moins 1400

33

1 400 à moins  1500

24

1500 et +

  6

N =

     200

III ) Remarques sur : « classe » , « classe modale », « centre de classe ».

11°)  Compléter  les  phrases suivantes :

Dans un tableau on donne  L'  effectif par ……………….  (qui est un "sous- effectif" )  ou un effectif par « ………………..» .

Cet effectif par classe ou caractère est noté par le  petit  " ……. " avec …………………………… : les   (n _i ) 

· On calculera  L' effectif total est la somme des éléments (n _i )  qui sont inventoriés . Le symbole désignant l'effectif total est  " N "

12°)  Compléter  la phrase : Lorsque le caractère est dit « continu » , ses éléments sont regroupés dans des « sous effectifs » que l’on appelle : ( ?) ………………..

Rappel : « Classe modale » :

13°)  Qu’appelle - t-on « classe modale » ?  

C.A.

(milliers d’euros )

     x _i

Effectifs

(  n _i )

L’effectif «  n ₃ » de la classe «  x ₃ » étant le plus grand .

La classe « x ₃ »  est la classe « modale » ;

    x ₁ =300 à moins  500

22

    x ₂ = 500 à moins  800

25

    x ₃ = 800 à moins  1 000

 n _{3  =}  90

    x ₄ = 1 000 à moins 1400

33

    x ₅ = 1 400 à moins  1500

24

     x ₆ = 1500 et +

  6

14°)  Compléter les phrases suivantes :

Remarques :

► pour tracer le polygone des effectifs  ou fréquences, il faudra rechercher pour chaque classe observée : « ………………. » .appelé aussi : « moyenne de centre de classe » ou « ………………………………………….».

► Dans le calcul de l’écart type  , on prendra la valeur centrale de chaque classe comme « x _i »

15°)  Compléter la phrase  : la valeur centrale est la valeur ……………….. de la classe.(calcul d’une moyenne).

Soit la classe :    [x _i ; x _i+1 [  , la valeur centrale sera le  Centre de classe :  x _icentrale

Classe :

Valeur centrale :

[ 300 ; 500[

On se souviendra que dans les calculs de l’écart type on « admet que les valeurs observées sont celles du centre de la classe ».

« Classe » et « amplitude »

16°)  Compléter la phrase  

La représentation graphique des effectifs d’une variable continue ( organisation de « classe » pour ranger ces effectifs)peut s’effectuer sous la forme ………………………………………………

Pour respecter le principe de construction de l’histogramme, on devra veiller à vérifier que les intervalles  de toutes les classes sont égaux.

, On dit que les classes doivent avoir la même amplitude.

17°) Compléter les intitulés Lsur les amplitudes)

Classes ……………………………….

Classe ………………………..

[ 300 ; 500[

Cette série ne sera pas exploitable pour tracer un …………... Il faudra repenser la distribution.    Voir « l’informaticien ».

[ 300 ; 500[

Cette série est exploitable pour tracer un ……………...

[ 500 ; 800[

[ 500 ; 700[

[ 800 ; 1000[

[ 700 ; 900[

[ 1000 ; 1400[

[ 900 ; 1100[

[ 1400 ; 1500[

[ 1100 ; 1300[

????

[ 1300 ; 1500[

IV ) FREQUENCE :

18°)  Compléter la phrase :

   Que faut-il connaître pour calculer le fréquence ?

.

19°) Donner la formule qui permet de calculer la fréquence exprimée sous forme décimale et sous forme d’un pourcentage  Ce rapport est noté :  f _i

Les mesures sont des observations qui informent :( VOIR EXEMPLE précédent ? ? ? ?° ):

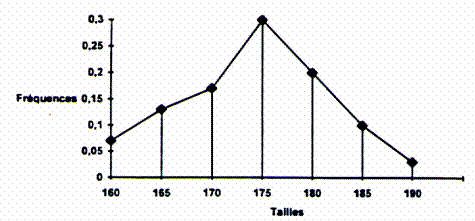
Des valeurs précédentes nous établissons le tableau suivant : (calcul des valeurs centrales et calcul des fréquences )

Commentaire :

En opérant le regroupement en intervalles, nous avons constitué 7 classes.

Dans chaque classe , les effectifs montrent le nombre d'événements produits  (l' événement est : taille - individu).

Si nous divisons l'effectif de chaque classe par le nombre de mesures (30), nous obtenons la

" Fréquence" de chaque classe.

Par définition : La fréquence d’une valeur de la variable statistique est le rapport de l’effectif de cette valeur à l’effectif total.

V)   Effectif simple  ( n_i ) et  effectif cumulé ( N_i )  et

     Fréquence simple  ( f_i )  et fréquence cumulée ( F_i )

Info ++

23°)  Compléter la phrase

  a) L’effectif simple et les fréquences simples  indiquent comment ………………………………. la variable  par rapport aux différentes modalités .

b) l’effectif cumulé et les fréquences cumulées  indiquent  comment ………………………… la variable par rapport  aux différentes modalités .

24°)  il existe par ailleurs deux catégories  de fréquences cumulées  :lesquelles , pour chaque : qu’indique - t- elle comme information?

-

Vous appuyer sur un exemple éventuellement .(utiliser le tableau ci dessous.)

exemple : soit un premier tableau représentant la distribution du chiffre d'affaires  ( C.A. )déclarés par les magasins d'un réseau de distribution d'une marque de textile .