|
|
|
|
|
|
|
|
|
CORRIGE. |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
||
|
|
LES
STATISTIQUES : TESTS niveau 5 |
|
||
Problème
n°1
|
SOS cours
1 : Calcul des fréquences |
|
SOS Cours 2 : le diagramme à bâtons |
|
|
|
Réponse tableau « a » :
3 ; 6 ; 7 ; 4 Réponse tableau « b » :
0,15 ; 0,30 ; 0,35 ; 0,20 Diagramme : ce sont des bâtons de
longueurs proportionnelles aux effectifs , avec
indication des fréquences. Fin du devoir 3 / 15 |
Problème
n°2
|
|
|
Réponse : 42 % |
Problème
3
|
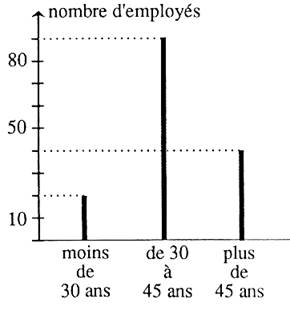
Les employés d’une entreprise se répartissent ainsi selon leur âge : Questions : Quel est le nombre total des
employés ? Réponse 150 Quel est, par rapport à ce nombre
total, le pourcentage des employés agés de 30 à 45 ans . Réponse : 60%, ou
0,60 et 60 Si 60% est identifié au
coefficient de proportionnalité 60 / 100 Alors 60 % = 0,60 mais à
la question : « quel est le pourcentage » on peut aussi
répondre : 60 !!
|
|
Problème n°4
|
N°4
|
||||||
|
Voici , pour les quatre trimestres de l’année
écoulé , les fréquences du nombre d’autos vendues par un garage (
fréquences données par rapport au
total des ventes de l’année , pour ce garage ) |
|
|||||
|
|
Numéro
du trimestre. |
1er |
2ème |
3ème |
4ème |
|
|
Fréquence
des ventes |
0,15 |
0,55 |
0,20 |
0,10 |
||
|
Fréquences
cumulées croissantes |
……0,15…….. |
……0,70….. |
……0,90…… |
……1…….. |
||
|
|
a)
compléter la dernière ligne du tableau |
|||||
|
b)
Par rapport aux ventes totales de 2002, quel est le pourcentage du nombre
d’autos vendues du 1er avril au 30 septembre ? réponse :
0,55 + 0,20 = 0,75 |
||||||
|
c)
Représenter les fréquences cumulées croissantes par un diagramme en bâtons ( ou un polygone) |
||||||
|
|
En abscisse on place les valeurs du caractère « x i »:
le trimestre. |
|||||
|
|
En ordonnée on met les fréquences
( f i ) La hauteur de chaque bâton est proportionnelle à la fréquence de
la valeur xi du caractère. |
|||||
|
|
|
|||||
Problème n°5
|
Voici la
répartition de notes dans une classe de 25 élèves : |
|||||
|
Notes « x » telles
que : |
5 < x |
5 £ x < 10 |
10 £ x < 15 |
15 £ x |
|
|
Fréquences de ces notes |
8% |
20 % |
48 % |
24% |
|
|
|
|||||
|
a) Combien d’élève
ont une note comprise entre 10 et 15 ? Réponse :
12 = 25 fois 0,48 |
|
||||
|
b) Combien
d’élève ont au moins une note
10 ? réponse :
25 fois ( 0,48 + 0,24) = 18 |
|||||
|
c) Combien
d’élèves ont moins de 15 ? réponse :
19 25
fois ( 0,08 +
0,2+0,48) = 19 |
|||||
|
d)
Représente les indications du tableau par un diagramme circulaire. (utiliser
le cercle tracé dans le cadre ci contre) |
|||||
|
Tracer des secteurs
angulaires et le diagramme est renseigné. 0 à 5 exclu : 360 fois 8 divisé par 100 = 28°8 5 inclus à 10 exclu :
3,6 fois 20 = 72° 10 inclus à 15 exclu :3,6 fois 48 =
172,8 ° 15 et au
dessus de 15 : 3,6 fois 24°= 86,4° la somme des secteurs = 360° |
|||||
Problème n°6
|
|
N°1
( SOS Cours )
|
|||||||||
|
|
Lors d’un contrôle , les masses exprimées en grammes de cent
exemplaires d’une bouteille de sirops sont classées de la manière
suivante : |
|||||||||
|
|
|
|
|
|
|
|||||
|
|
Masse (g) |
Effectif n i |
Valeur
centrale : « x i » |
|
Produit n i x i |
|
||||
|
|
[
804 ; 806 [ |
3 |
805 |
|
2415 |
|
||||
|
|
[
806 ; 808 [ |
4 |
807 |
|
3228 |
|
||||
|
|
[
808 ; 810 [ |
46 |
809 |
|
37214 |
|
||||
|
|
[
810 ; 812 [ |
38 |
811 |
|
30818 |
|
||||
|
|
[
812 ; 814 [ |
7 |
813 |
|
5691 |
|
||||
|
|
[
814 ; 816 [ |
2 |
815 |
|
1630 |
|
||||
|
|
|
Total :
Ni |
100 |
|
Total :
des n i x i |
80996 |
|
|||
|
|
On demande
de calculer : |
|||||||||
|
|
1°) La masse
moyenne d’une bouteille : masse
moyenne : 80996
/ 100 = |
|||||||||
|
|
Compléter
le tableau ( centre de classe , produits) |
|||||||||
|
|
2) L’ écart
type : s (
SOS Cours ) |
|||||||||
|
|
Ne pas
confondre « variance »
et « écart
type » : Calcul de
la variance : Calcul de
l’écart type : Réponse : 1 ,
75 |
|||||||||
|
|
|
|
|
|
|
|||||
|
|
Masse (g) |
Effectif |
Valeur
centrale : |
|
|
|
||||
|
|
[ 804 ;
806 [ |
3 |
805 |
3 ( 805 -
810)² |
25 fois3= 75 |
|
||||
|
|
[
806 ; 808 [ |
4 |
807 |
4 ( 807 -
810)² |
36 |
|
||||
|
|
[ 808 ; 810
[ |
46 |
809 |
46 ( 809 -
810)² |
46 |
|
||||
|
|
[
810 ; 812 [ |
38 |
811 |
38 ( 811 -
810)² |
38 |
|
||||
|
|
[
812 ; 814 [ |
7 |
813 |
7 ( 813 -
810)² |
63 |
|
||||
|
|
[
814 ; 816 [ |
2 |
815 |
2 ( 815 -
810)² |
50 |
|
||||
|
|
|
|
100 |
|
|
308 |
|
|||
|
|
|
V = 308 / 100 = 3,08 |
|
s = |
|
|||||
Problème n°7
|
N°3 : (
SOS Cours ) |
|
|
|
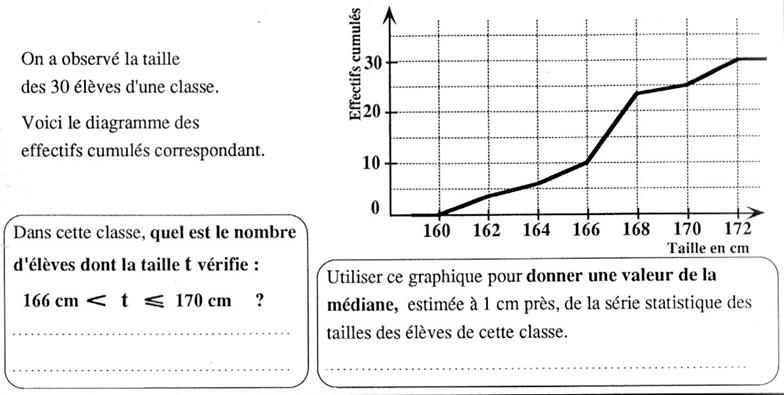
Réponse : 1°) le nombre d’élèves dont la taille est 166 < t ≤ 170
est de 15 2°) la valeur de la médiane est toute valeur appartenant [166 ; 168 ] |
Problème n°8
|
2-
|
Dans
une classe de 40 élèves , la moyenne
d’un devoir était 10,6. En
fait, le professeur avait oublié 1 point à 2 élèves. Question : Quelle est , en réalité, la moyenne de la
classe ? |
|
|
Première solution : ( 40 fois
10 ,6 ) + 2 = 424 + 2 = 426 nouvelle moyenne : 426
/ 40 = 10,65 Deuxième solution : on rajoute 2 / 40 à la note soit 0,05 La nouvelle moyenne est de
10,65 |
Problème n° 9
|
|
N°2 : (
SOS Cours ) |
|
|
|
Dans une entreprise
, la répartition des salaires , pour une semaine de 35 heures est la
suivante : -
salaire
compris entre 2 00 € et 600 € : 51 personnes -
salaire
compris entre 600 € et 1 000
€ : 5 personnes. -
Salaire
compris entre 1 000 € et 1400 € 5
personnes. -
Salaire
compris entre 1 400 € et 1 800 € : 40 personnes. En
utilisant les centres de classes , le patron de l’entreprise a calculer une
estimation du salaire moyen. 1°) Combien
a - t- il trouvé ? ( Sos Cours) réponse : 934,60 €.
|
|
|
|
2°)Les
syndicats disent : le salaire médian n’est que de 600 €. ( Salaire
médian signifie : médiane de la série statistique des salaires) EST - CE -
POSSIBLE ? Oui . , il suffit de
calculer la médiane de la masse salariale. |
|
Problème n°10
|
|
N°6 : (
SOS Cours ) |
|
|||||||||||||||||||||||||
|
|
Dans une
maison individuelle ayant un chauffage bi - énergie ( fioul + électricité) ,
on a noté pendant la saison de chauffage
2002 - 2003 les indications suivantes du compteur électrique ( en k w
h) : |
|
|
||||||||||||||||||||||||
|
date |
1/09/ 2002 |
1/10/ 2002 |
1/11/ 2002 |
1/12/ 2002 |
1/01/ 2003 |
1/02/ 2003 |
1/03/ 2003 |
1/04/ 2003 |
1/05/ 2003 |
1/06/ 2003 |
1/07/ 2003 |
1/08/ 2003 |
1/09/ 2003 |
||||||||||||||
|
Index
au compteur |
56178 |
56
874 |
58
093 |
61
100 |
63
803 |
65
963 |
68
738 |
71
194 |
73
194 |
75
270 |
75
972 |
76 413 |
76
691 |
||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
1°)
Calculer les consommations mensuelles
et cumulées d’électricité : |
|
|||||||||||||||||||||||||
|
mois |
sept |
oct |
nov |
déc |
jan |
fév |
mar |
avr |
mai |
juin |
juil |
août |
|||||||||||||||
|
Consommation mensuelle |
696 |
1219 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
Consommation
cumulée |
696 |
1915 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
Consommation mensuelle et cumulée: Pour
le mois de sept : 56 874 - 56 178 = 696
; Cons. Cumul sept. 696 Pour
le mois d’oct
: 58 093 - 56 874 = 1 219
; Cons. Cumul. oct : ( 1 219 - 696 =1915 ) ou (
58 093 - 56 178 = 1915) Et
ainsi de suite. |
|
|||||||||||||||||||||||||
|
|
2°) faire le diagramme polaire de la
consommation mensuelle : laisser
les traits de construction. ( sos
cours) construction
avec un compas ; choisir une échelle judicieuse. !!!! |
|
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
Problème 11.
|
|
|
|
4 |
|
|
|
Nous ne devons donner que des valeurs
approchées : Sur les angles : c’est une indication. Les valeurs recherchées en valeurs approchées
, acceptées sont : Afrique :180 + ou - « 2 millions » Asie : 120 + ou - « 2 millions » Amérique : 420 + ou - « 2 millions » |