|
Les
angles |
|
1.
Définitions. |
|
|
|
2. Angles
particuliers.
|
|
|
|
3. Le rapporteur. |
|
|
|
4. Cosinus d'un angle
aigu.
|
|
|
|
5.
|
|
|
|
6.
|
|
|
|
7.
|
|
|
|
8.
|
|
|
|
9. Angles égaux. |
|
|
|
10.
Calculs sur les angles. |
|
|
|
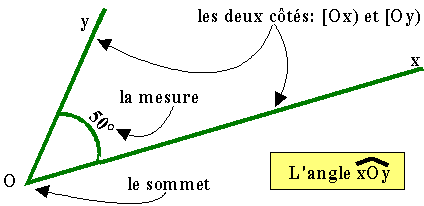
Un angle a
un sommet et deux côtés. La mesure
d'un angle ne dépend pas de la longueur de ses côtés. Elle dépend de
l'écartement des côtés. Les unités de mesure sont le degré(°), le grade(gr) et le radian(rd). L'outil de mesure est le rapporteur. |
|
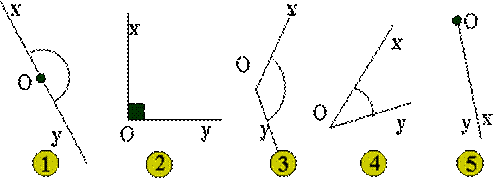
Selon leur mesure:
|
1. l'angle plat: 180° 2. l'angle droit: 90° 3. l'angle obtus:
entre 90° et 180° 4. l'angle aigu: entre
0° et 90° 5. l'angle nul: 0° Un
angle saillant a une mesure inférieure à 180°. Si cette mesure est supérieure
à 180° alors l'angle est rentrant |
|
Selon leur position:
|
1. les angles opposés
par le sommet 2. les angles
adjacents 3. l'angle au centre
(sommet au centre d'un cercle) 4. les angles alternes
internes 5. les angles alternes
externes 6. les angles
correspondants
|
|
Notes:
Les
angles opposés par le sommet sont toujours égaux.
Deux
angles sont adjacents lorsqu'ils respectent trois conditions:
- avoir le même sommet.
- avoir un côté commun.
- les deuxièmes côtés de part et
d'autre du côté commun.
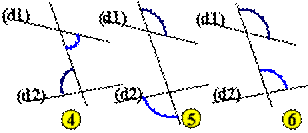
Les
droites (d1) et (d2) ne sont pas parallèles. Dans ce cas, les angles alternes
ne sont pas égaux ainsi que les angles correspondants. Voir le cas particulier
des bandes à bords parallèles.
Selon la
somme des mesures de deux angles, nous distinguons:
1.
les
angles complémentaires dont la somme des mesures est égale à 90°. Exemple: 70°
et 20°.
2.
les
angles supplémentaires dont la somme des mesures est égale à 180°. Exemple: 50°
et 130°.
|
Le
rapporteur: |
|
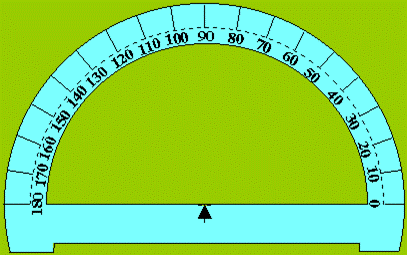
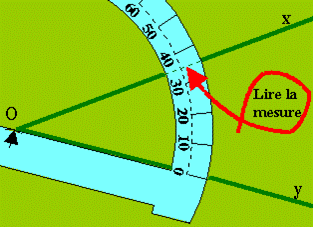
Le dessin
ci-contre représente un rapporteur gradué en degrés (de 10 en 10 ici; celui
que vous possédez doit l'être de degré en degré). La flèche noire indique le
centre du rapporteur. La droite qui passe par les graduations 0° et 180° est
un diamètre du rapporteur. Lors de la mesure d'un angle, le centre du
rapporteur doit être au sommet de l'angle, le diamètre doit être confondu
avec l'un des côtés de l'angle. |
|
|
1. Mesurer un angle donné: L'angle
étant tracé, placez le centre du rapporteur sur le sommet de l'angle, faites
coïncider le diamètre du rapporteur avec l'un des côtés de l'angle: [Oy) sur notre exemple. Lisez la mesure en face de la
graduation qui se trouve en vis à vis du deuxième côté [Ox). |
|
|
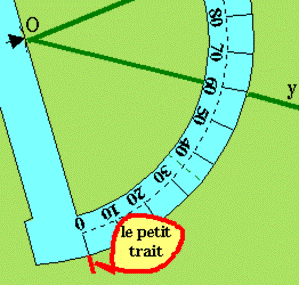
2. Tracer un angle de mesure donnée: Il
est nécessaire qu'un côté soit tracé: [Oy) par
exemple. La manipulation est la même qu'au 1 si le deuxième côté doit se
trouver du côté du rapporteur lorsque son diamètre est confondu avec le
premier côté. Mais
si nous voulons tracer l'angle de côtés [Oy) et
[Oz) avec [Oz) "dessous" [Oy), il faut
opérer de manière un peu différente: tournez le rapporteur autour de son
centre de façon à ce que la graduation désirée (60° sur notre exemple
illustré par la deuxième figure ci-contre) soit en vis à vis avec [Oy). Tracez un petit trait en face du 0°. Enlevez le
rapporteur, joignez le point O au petit trait et prolongez pour obtenir [Oz). |
|
|
Cosinus d'un angle aigu: |
@ INFO
++++ |
|
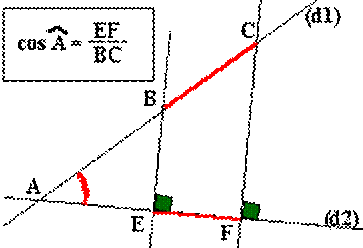
Les
droites (d1) et (d2) sont sécantes en un point A et déterminent un angle aigu. B et C
sont deux points quelconques de (d1). Deux
droites parallèles passant par B et C coupent orthogonalement (d2) en E et F. 1.
Définition: Le cosinus
de l'angle A est le rapport de EF sur BC. 2.
Remarques:
|
|
|
3.
Application au triangle rectangle: Sur la
première figure nous pouvons construire un triangle rectangle: en traçant une
droite parallèle à (d2) et passant par B. Cette droite coupe (CF) en H. Comme
(BH) et (EF) sont parallèles et (CF) est perpendiculaire à (EF) alors (CF)
est perpendiculaire à (BH). Nous avons notre triangle rectangle: BCH
rectangle H. De plus:
comme BHFE a trois angles droits alors BHFE est un rectangle. Comme BHFE est
un rectangle alors BH=EF. Dans le
triangle rectangle BCH le cosinus de l'angle B est donc le rapport entre le
côté adjacent à l'angle B sur l'hypoténuse. 4.Remarques: Dans un
triangle rectangle il y a un angle droit et deux angles aigus. Ces deux
angles aigus ont un côté commun qui est l'hypoténuse. Leur deuxième côté est
celui qui est appelé côté adjacent. Par suite le cosinus de l'angle C,
dans le triangle rectangle BCH est le rapport CH sur BC. |
|
5.Valeurs particulières:
Dans un
triangle rectangle le cosinus est toujours obtenu en divisant par le côté le
plus long du triangle rectangle, c'est à dire l'hypoténuse. Encore une fois: le
cosinus d'un angle est inférieur à 1 ou égale à 1 lorsque l'angle mesure 0°
(angle nul).
Lorsque
l'angle mesure 90° (angle droit) son cosinus est égale à 0.
6.
Calculs avec le cosinus d'un angle:
calcul du cosinus:
Si nous
connaissons la mesure de l'angle, il est très facile avec une calculatrice de
calculer son cosinus: calculer cos 40° se fait en tapant 40 suivi de la touche cos.
Vérifiez bien avant d'utiliser votre calculatrice qu'elle est bien en
"mode" degrés (voir éventuellement la documentation de votre
machine).
calcul de l'angle:
Si nous
connaissons le cosinus de l'angle, il faut utiliser une touche supplémentaire
qui dépend de la calculatrice: elle se nomme 2nd ou INV ou...(voir la documentation! ce sont là les appellations les
plus courantes). Soit l'angle dont le cosinus est 0,715. Entrez ce nombre,
appuyez sur la touche 2nd (par exemple) et sur la touche cos. Vous devriez
obtenir: 44,35680...en degrés.
Calcul d'un côté de triangle rectangle:
Si
le triangle ABC est rectangle en A et que la mesure de l'angle B est connue,
vous pouvez calculer BC si vous connaissez aussi AB (ou calculer AB si vous
connaissez aussi BC).
Si
c'est l'angle C qui est connu, les égalités suivantes seront correctes lorsque
vous aurez remplacé l'angle B par l'angle C, le côté AB par le côté AC. Le côté
BC étant l'hypoténuse, la place de sa mesure dans les formules est la même.
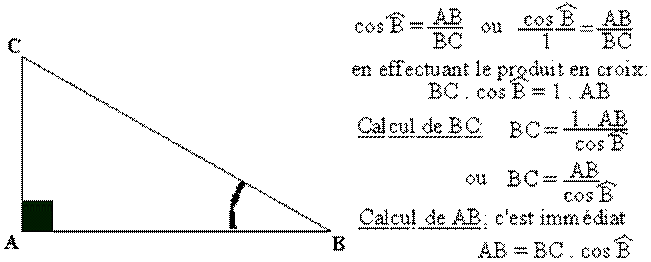
!!! Ces
calculs ne sont valables que dans un triangle rectangle !!!
Angles
égaux:
Vous
trouverez des angles égaux:
- avec la bissectrice d'un angle.
- pour les angles opposés d'un parallélogramme.
- dans un triangle équilatéral ou
isocèle
- lorsque des droites parallèles
sont coupées par une sécante
- si ils sont aigus et
ont même cosinus
Calculs
sur les angles:
Vous pouvez
effectuer de nombreuses opérations sur les mesures d'angles.
Si vous
connaissez le cosinus d'un angle aigu vous pouvez en déterminer la mesure.
En utilisant
la somme des angles d'un triangle (égale à 180°), il est souvent possible de
déterminer la mesure x d'un angle en connaissant la somme des mesures des deux
autres angles du triangle (x=180-somme).