corrigé CONTROLE:
1°) Donner la forme d’une équation de droite. L’équation est de
la forme « y = ax
+b »
2° ) Donner la procédure permettant de tracer une droite à partir
d’une équation.
|
Equation théorique : y =
m x + p |
|
|
1°) on donne ou choisi deux
valeurs à « x » ; x 1 et x 2 |
|
|
2°)on
calcule les valeurs correspondantes y 1 et y 2 |
|
|
3°) on place les points M 1 et M 2 |
|
|
4°) on trace la droite passant par M 1 M 2 |
|
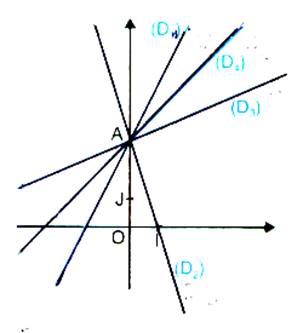
Première série de tracés :
On a tracé les quatre
droites (D1) ; (D2) ;
(D3) ; (D4) suivantes données par leur équation de
la forme : y = mx + p
|
|
|
|
(D1) ; y = 2 x + 3 |
|
|
(D2) ; y = -3x +3 |
|
|
(D3) ; y = |
|
|
(D4 ; y = x +3 |
Que constate-t-on ?
on constate qu’elles ont un point commun
;
Quelles sont les coordonnées du point
« commun » ? les coordonnées du
point A est ( 0 ;+3)
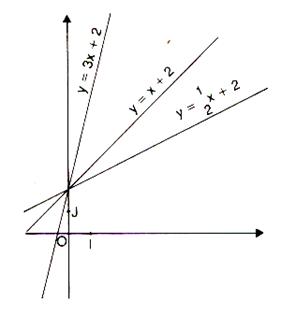
Deuxième série de
tracés :
Tracer les trois droites
(D1) ; (D2) ; (D3) ;
suivantes données par leur équation de la forme : y = mx
+ p
|
(D1) |
(D2) |
(D3) |
|
|
y = 3 x +
2 |
y = x + 2 |
y = |
|
|
|
|||
Imaginons que ces droites
représentent le profil d’une route en
montagne.
Classer dans l’ordre croissant
de celle qui monte le moins à celle qui monte le plus
: (D3) ; (D2) ; (D1)
Que est la relation ( valeur ) dans
l’équation qui lie l’inclinaison ; la
« pente » et le tracé : ![]() ;
1 ; 3
;
1 ; 3
Comparer les valeurs numériques et ces inclinaisons de
droites : plus
le nombre est grand plus la pente ( l’inclinaison) est grande .
On obtient deux classements identiques ,
le coefficient « m » de l’équation
y = mx + p renseigne sur la direction de la
droite .
Définition
du coefficient directeur :
Si une droite a pour
équation y = m x + p ,
le nombre « m » est appelé « coefficient directeur de la
droite »
Remarque : le
coefficient directeur peut être positif ou négatif.
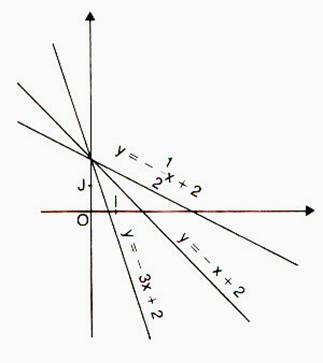
troisième série de tracés :
Tracer les trois droites
(D1) ; (D2) ; (D3) ;
suivantes données par leur équation de la forme : y = mx
+ p
|
(D1) |
(D2) |
(D3) |
|
|
y = -3 x + 2 |
y = - x + 2 |
y = - |
|
|
|
|||
Imaginons que ces droites
représentent le profil d’une route en
montagne.
Classer dans l’ordre de celle qui descend le moins à celle qui monte le plus .
Que est la relation ( valeur ) qui lie la « pente » et le tracé.