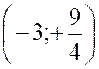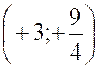|
OBJECTIFS : - Savoir |
I ) Pré requis:
|
|
|
|
|
i9 |
:i |
|
|
i9 |
:i |
|
|
|
|
|
|
|
|
|
|
|
|
|
II ) ENVIRONNEMENT du dossier :
|
Dossier précédent : |
Dossier
suivant : |
Généralités : |
|
|
|
|
|
|
III
) LECON n° : ETUDE DE LA FONCTION : y =
a x²
|
|
|
|
|
|
1.
Etude d’un
cas. (exemple : « y = |
|
|
|
2.
Etude d’un
cas. (exemple : « y = - 2
x² » ) |
|
|
|
|
|
|
|
3.
Cas général . |
|
IV) INFORMATIONS « formation leçon » :
|
|
Travaux auto - formation. |
|
Corrigé des travaux auto - formation. |
|||
|
Contrôle |
évaluation |
|||||
|
|
|
|
|
|
|
|
V ) DEVOIRS ( écrits):
|
Devoir diagnostique L tests. |
|
|
Devoir Auto
- formatif
(intégré au cours) |
|
|
Devoir Formatif « Contrôle :
savoir » ; (remédiation) |
|
|
|
|
|
Devoir sommatif. |
|
|
Devoir certificatif : (remédiation) |
|
* remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour conclure une formation .
|
Leçon |
Titre ETUDE DE LA FONCTION : y = x² |
|
N° |
|
|
Exemple
d’un cas n°1 : |
|
|
Exemple : Etude de la fonction : « y = |
|
|
Cette fonction est définie pour : « - |
|
|
|
|
|
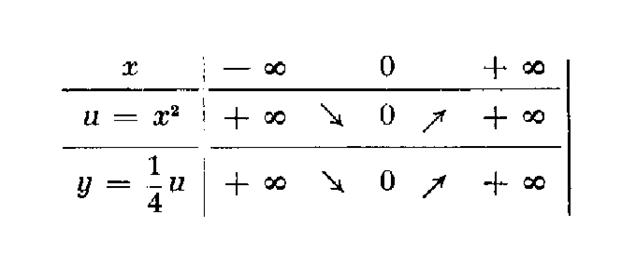
Posons « u = x² ». Le nombre « u » varie dans le
même sens que « x » ou en un sens contraire selon que
« x » est positif ou négatif.
Or : « y = D’où le tableau de
variation ci-contre. |
|
|
|
|
|
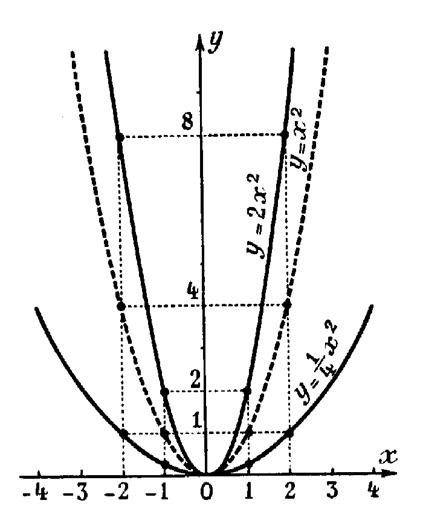
Représentation graphique . |
|
|
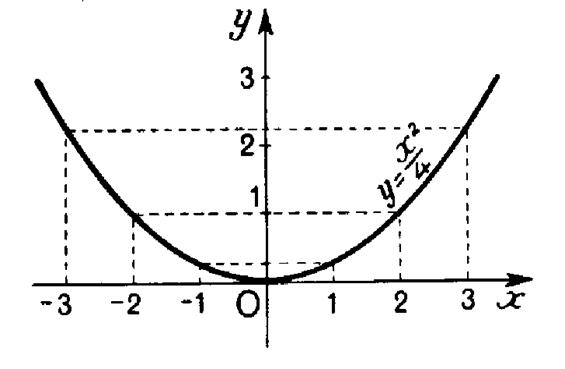
Dans un repère cartésien ortho normal
construisons les points de coordonnées :
Voir ci contre…. Nous obtenons une parabole de la forme « y = x² ) mais plus évasée. . Elle admet l’origine « O » pour sommet ,
« y y ‘ » pour axe de symétrie et tourne
sa « concavité» vers les « y » positifs. On peut l’obtenir en divisant par « 4 » ,
pour chaque valeur de « x » , l’ordonnée du point correspondant de
la parabole « y = x² » |
|
|
Etude du
cas n° 2 : |
|
|
Exemple : Etude de la fonction : « y = - 2 x² » |
|
|
|
|
|
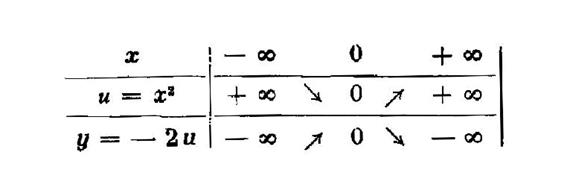
Posons « u = x² ». Le nombre « u » varie dans le
même sens que « x » ou en un sens contraire selon que
« x » est positif ou négatif.
Or : « y = -2 u » est une fonction linéaire de
« u » à coefficient négatif « -2 », donc « y »
varie dans le sens contraire de
« u ». D’où le tableau de
variation ci-contre. |
|
|
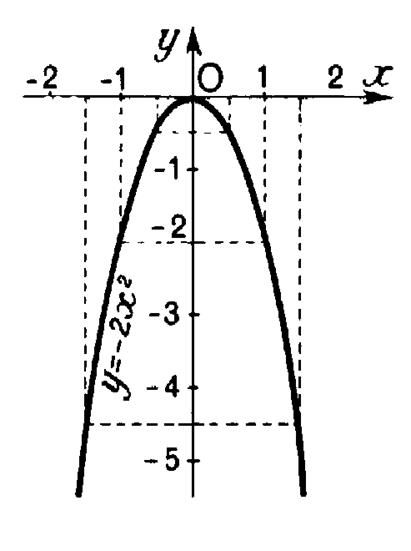
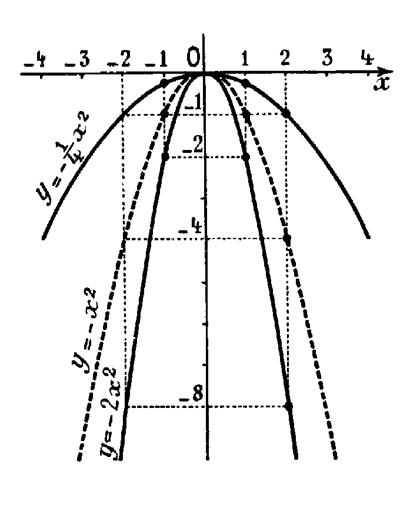
Représentation graphique . |
|
|
Par rapport à deux axes ortho normaux , construisons les points de coordonnées : ( 0 ; 0 ) ; ( + 1 ; - 2 ) ; (
-1 ; -2 ) ; Nous obtenons une parabole de la forme « y = x² ) mais moins évasée et tournant sa concavité
vers les « y » négatifs. On peut aussi l’obtenir en multipliant
par « -2 » , pour chaque valeur de
« x » , l’ordonnée du point correspondant de la parabole « y = x² » . |
|
|
Cas général . |
|
|
La
fonction « y = a x² » est
définie pour : « - |
|
|
|
|
|
Le nombre « u » varie dans le même sens que
« x » ou en sens contraire
suivant que « x » est positif ou négatif. Or « y = a.u » est une fonction
linéaire de « u » qui varie dans le même sens que « u » si « a » est
positif ; en sens contraire de « u » si « a » est négatif. On obtient : |
|
|
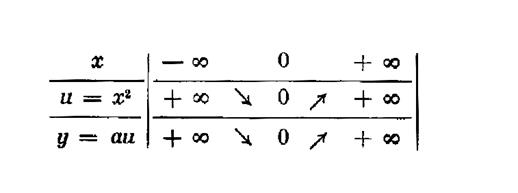
1°) « a » est positif |
|
|
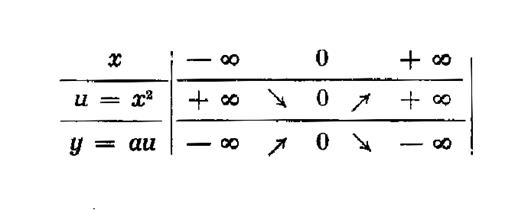
Tableau de
variation : |
Représentation
graphique : |
|
Pour « a »
positif : 1°) La fonction admet avec « x= 0 » un
minimum ( y
) égal « 0 »
2°) on remarque que pour « x |
1°) La courbe est une parabole de sommet « O » et d’axe
« y ‘ y » 2°) Pour tous les « a »
positifs ; la concavité
de la parabole est du côté des « y » positifs.
|
|
1°) « a » est négatif |
|
|
Tableau de
variation : |
Représentation
graphique : |
|
Pour « a »
négatif : 1°) La fonction admet avec « x= 0 » un
maximum ( y ) égal « 0 ».
2°) on remarque que pour « x |
1°) La courbe est une parabole de sommet « O » et d’axe
« y ‘ y » 2°) Pour tous les « a »
négatifs ; la concavité
de la parabole est du côté des « y » négatifs .
|
|
|
|
|
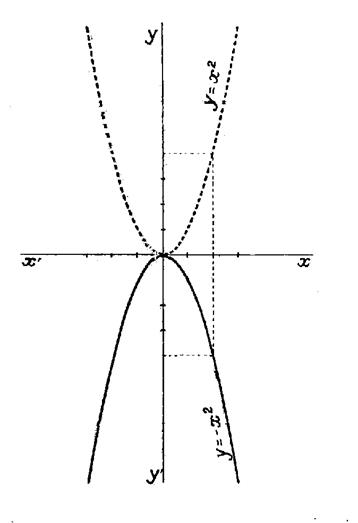
Remarque : Les paraboles « y = a x ² »
et « y = - a x² »
tracées sur un même graphique . ( voir ci- contre) sont symétriques par rapport à l’axe « x ‘ x » : Il en est ainsi des paraboles : Pour « a » = « +1 » ; dans « y = + x² » et
Pour « a » = « - 1 » ; dans « y = - x² » Ou « y = - 2
x² » et « y = 2 x² » …(voir ci-dessus) |
|
|
|
|
|
Leçon |
Titre |
|
N° |
TRAVAUX d ’ AUTO
- FORMATION sur ETUDE DE LA
FONCTION : y = x² |
A venir
Compléter
le tableau suivant :
|
|
- 10 |
- 5 |
-2 |
-1 |
0 |
+1 |
|
+5 |
|
|
|
|
|
|
|
|
|
+4 |
|
+100 |
Faire la
représentation graphique .