@

Leçon

Titre

N°4

TRAVAUX d ’ AUTO - FORMATION sur « PUISSANCES » et « RACINES »  avec des nombres décimaux positifs . ( D +)

 

TRAVAUX  N° 4   d ’ AUTO - FORMATION  CORRIGE  : CONTROLE

 

 

  1°)A quoi est égal le carré d’un nombre ?

Le « carré d’un nombre » est égal au  produit de ce nombre par lui-même .

 

   2°) A quoi est égal le cube d’un nombre ?

Le « cube »  d’un nombre est égal au  produit de trois facteurs égaux à ce nombre.

 

    3°) A quelle opération  correspond  l’écriture 10 n , et quelle forme décimale  prendra - t - elle ?

 

10 n

=

10 10  10 1010… n 

 

 ( « n » facteurs)

;

L’écriture décimale est un « 1 » suivi de  « n » zéros

 

    4°) A quoi correspond l’écriture scientifique ( quelle forme) ?

 

L’écriture scientifique d’un nombre est l’écriture de ce nombre sous la forme  «  a 10n »  où « a » est un nombre qui s’écrit avec un seul chiffre (différent de zéro) avant la virgule .

 

5°) Qu’est ce que la « racine carré d’un nombre » ? Comment la note t-on ?

La racine carrée de « a » est le nombre qui , élevé au carré , donne « a ».

Notation :    . on lit « racine de  a    » , ou « racine carré de « a »

 

Nota : la « vraie notation est : 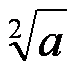 ;  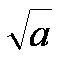est une écriture « simplifiée ».

 

 6°) Quelles sont les  possibilités qui permettent d’obtenir la valeur numérique de  la racine carrée d’un nombre ?

Pour obtenir la racine carrée d’un nombre on utilise généralement la calculatrice ;

ou une table numérique ;

ou alors on fait le calcul qui s’appelle : «  extraire la racine ».

 

 

TRAVAUX N° 4    d ‘ AUTO - FORMATION EVALUATION

 

Exercices :

CARRE :

Série 1 :  Ecrire les puissances sous forme de produits :

 7,4² =  7 ,4 ´  7,4

 25² =   25 ´ 25

0,2² =  0,2 ´ 0,2

 

Série 2 : calculer les carrés des nombres suivants : (à faire en calcul mental )

 

résultat

 

 

Résultat

1² =

1

 

5² =

25

4²  =

16

 

8² =

64

7²  =

49

 

10 ² =

100

9²  =

81

 

6² =

36

3²  =

9

 

2² =

4

 

Série 3 : calculer les carrés des nombres suivants 

 601 ² =

361201

 

 0,63 ² =

0,3969

79,76 ² =

6361,6576

 

0,247²  =

0,061009

7,459 ² =

55,636681

 

0,99 ² =

0,9801

 

Série 4 :  Compléter le tableau :

 X

 3

 13

15,7

 3,5

0,5

0,1

 X²

9

169

246,49

12,25

0,25

0,01

 

 

CUBE :

Série 1 :  Ecrire les puissances sous forme de produits :

7,4 3 =  7 ,4 ´  7,4´  7,4

253 =   25 ´ 25´ 25

0,23 =  0,2 ´ 0,2´ 0,2

 

Série 2 :

13  =

1

 

43  =

64

23  =

8

 

53  =

125

33  =

27

 

103  =

1 000

Série 3 :

 

Calcul à la main

A la calculatrice .arrondir évent. au millième

43  =

64

 

0,53  =

0,125

0,125

6,253  =

244,140625

244,141

1,193  =

1,685159

1,685

0,833  =

0,571787

0,572

72,53  =

381078,125

381078,125

132, 43  =

2320940,224

2320940,224

 

Série 4 : Compléter le tableau

X

2

3

10

15

4,5

0,5

0,1

X3

8

27

1 000

3375

91,125

0,125

0,001

 

 

 

 

 

LES PUISSANCES DE 10 :

 

Série 1 : donner l’écriture décimale des nombres suivants :

           ( exemple : 210 -2 =2 0,01 =  0,02  )

 

Résultat

 

 

Résultat

610 -² =

0,06

 

1,3210 -3 =

0,00132

710 -4 =

0,0007

 

4,510 -1 =

 0,45

 

 

 

Série 2 : donner l’écriture décimale des nombres suivants :

           ( exemple : 210 3 =2 1 000 = 2000 )

 

Résultat

 

 

Résultat

6   10 ² =

600

 

1,32  10 3 =

 1320

7 10 4 =

70  000

 

4,5  10 ² =

 450

 

Série 3 : les nombres suivants sont lus sur l’écran d’une calculatrice . Donner pour chacun d’eux l’écriture scientifique , puis l’écriture décimale .

 

Ecran  de calculatrice :

Non normalisée

l’écriture scientifique

l’écriture décimale

Ex. 5,1302

= 5,12  100

= 512

1,504

1,5  10 000

15 000

7,3503

7,35 1000

 7 350

9,0405

9,04  100 000

 904 000

 

Ecriture scientifique :

 

Série 1 : Donner l’écriture scientifiques des nombres suivants :

 
Passage intermédiaire

Ecriture scientifique

Ex. 1653 =

1,653  1 000

= 1,653 103

346,3 =

3,463 100

= 3,463 10 ²

7 000 =

7  1 000

= 7  103

20 000 =

2  10 000

=  2 104

542 000 =

5,42  100 000

= 5,42  105

 

Série 2 : Pour les nombres suivants , passer de l’écriture scientifique à l’écriture décimale .

 

Ecriture scientifique

Passage intermédiaire

Ecriture décimale

Ex. 5,24  102

5,24 100

 = 524

3,4  103

3,4  1000

= 3 400

 6,467 104

6,467 10 000

= 64 670

9,674 106

9,674 1 000 000

= 9 674 000

1,135  102

1,135  100

= 113, 5

 

 

 

 

Série 3 : Pour les nombres suivants , passer de l’écriture scientifique à l’écriture décimale .

 

Ecriture scientifique

Passage intermédiaire

Ecriture décimale

Ex. 5,24  10-2

5,24 : 100

 = 0,0524

3,4  10-3

3,4 : 1 000

 = 0,0034

 6,4 10-4

6,4 :  10 000

 = 0,000 64

9,67 10-2

9,67 : 100

= 0,0967

1,135  10-2

1,135 : 100

= 113,5

 

Série 4 : Ecrire les nombres suivants en écriture scientifique .

1675,73

1, 67573 103

 

0 ,03

3  10-2

0,007 89

7,8910-3

 

79 632

7,9632  104

52,704

5, 2704 10

 

0,000 3

3  10-4

 

Série 5 : Ecrire les nombres suivants en écriture scientifique .( puissances négatives)

0,054

5,4  10-2

 

0,000 01

 1  10-5

0,379

3,79 10-1

 

0,000 67

6,7  10-4

0,31

3,1 10-1

 

0,007 3

 7,3 10-3

 

RACINES CARREES :

 

Série 1 . Calculer les racines carrées suivantes : ( sans calculatrice)

 

 

Résultat

 

 

Résultat

3

 

 6

4

 

8

5

 

9

10

 

1

 

Série 2 : Calculer les racines carrées suivantes . On utilisera la touche  de la calculatrice . Faire la vérification ( le carré du résultat)

 =

= 2,8

  =

= 27

 

Série 3 : Calculer les racines carrées suivantes , on utilisera la touche  de la calculatrice . , on arrondira  au 0,01  près.

 =

 1,09

  =

7,30

Série 4 : Calculer les racines carrées suivantes ,on utilisera la touche  de la calculatrice . , on arrondira  au 0,001  près.

 =

1,732

 =

1,414

  =

1,581

 

Série 5 :

Compléter  le tableau :

x

5

6

1000

4,5

0,5

0,1

 

2,236

2,449

10

2,121

0,707

0,316

 

PROBLEMES divers : Voir application  aire du carré ; Pythagore , le volume du cube .

 

 

 

CORRIGE  des  TESTS  Série 2 : niveau ++++

1°)   Cochez Vrai ou Faux

 

 

Vrai

Faux

a)      

 n’existe pas

 

: » 1,732…

a)      

  = 0,3

 

  = 0,3

et   = 0,948…

b)      

3 <    <  4

3² < 13< 4²

 

c)       

  n’existe pas

 Car 2 -p < 0

 

d)      

L’opposé de  est  

 

L’opposé de

 est -

e)      

  =  4

 

4 est la moitié de 8 et non sa racine.

f)         

 = 10²

( 10²)² = 104

 

g)      

 ( )4  =  10²

´´´ = 10 ´ 10 = 100 = 10²

 

 

2° )  Souligner  les écritures  qui désignent  le nombre 5 et encadrez celles qui désignent  le nombre - 5

 

 ;  -  ;  ;  ; ( )²  ; ()² ; (-)² ;

Réponses

 : 5 =  ; ()² ; (-)² ;

Et  - 5 =   -  

 

Les trois écritures n’ont pas de sens :  ;  ; ( )²

3°) Répondez et justifiez :

les nombres suivants sont-ils égaux ?  OUI ou NON

  ;    ;    ;

corrigé :

· =   =

 

· =  =

 

·=  =  ==   conclusion les nombres sont tous égaux.
4° )  Cochez la bonne réponse /

quelle est ou  quelles sont   les  ou la solution   des équations suivantes ?

 

Equations

A

B

C

1°)

( ) ²  = 7

7

49

2°)

x²     =  7

7 et -7

   et  -

49

3°)

 = 7

7 et -7

   et  -

49

4°)

 = 7

7 et -7

   et  -

49

 

5°) Compléter les pointillés par un nombre entier ou décimal :

 

Calculs :

4  = ………..´

4  = …4 ´ = 4 ´.´ = 4´2´ = 8

 

 

  -   =  ………..´

 -  =  - = 3 - 5 =

 ( 3 -5) =  -2

 

 

3   ´  5  = …………..´

3   ´  5  =3´´   ´  5 ´=

             =   3´  5 ´´´

´ = 3

           = 3´  5 ´3´  = 45

 

 

 .´  = ….´

 .´  = .´ ==