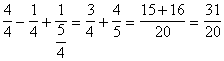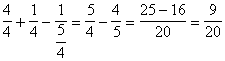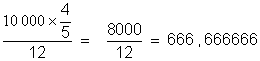Retour
vers les exercices et 44 problèmes ◄◄◄
|
|
|
LES
FRACTIONS : EXERCICES et
PROBLEMES : |
|
CORRIGE des situations exercices types problèmes :
|
EXERCICES TYPES débouchant sur des PROBLEMES TYPES. |
||
|
1 |
Les ¾ d ’ un nombre égal 15 .Quel est ce nombre ? |
(15 fois 3 ) : 4 = 11,25 |
|
2 |
le nombre + 1/3 du
nombre = 24 . Quel est ce nombre ? rép. 18 |
4/3 de ce
nombre = 24 donc : 24 : ( 4/3) = 24 fois 3 divisé par 4 = 18 |
|
3 |
1/3 du nombre + 2/5 du nombre = 44 . Quel est ce
nombre ? rép. 60 |
1/3 + 2/5 = 11/15 de ce nombre représente
44 ; donc ce nombre vaut 44 : ( 11 / 15) = (44 fois 15 ) divisé par 11 = 60 |
|
4 |
¾ du nombre + 1/3 du nombre = 26. Quel est ce
nombre ? rép.24 |
3/4 + 1/3 = 13 / 12 de ce nombre représente 25. Ce nombre vaut : 26 : ( 13 /12) soit 25 fois 12 divisé par 13 |
|
5 |
¼ du nombre + 20 = 36 . Quel est ce nombre ? Rép.= 64 |
16 représente le 1/4 du nombre . On en déduit
que ce nombre vaut 16 fois 4 = 64 |
|
6 |
3/5 du nombre -15 = 21. Quel est ce nombre ? |
Les 3/5 de ce nombre vaut 36 Ce nombre vaut : 36 : ( 3/5) = 60 |
|
7 |
Les ¾ des 5/7 d ’ un nombre valent 45. Quel est ce
nombre ? |
Les 15 / 28 de ce nombre vaut 45 Donc ce nombre vaut : 45 / ( 15 /28) soit
= 84 |
|
8 |
Trouver un nombre qui , augmenté de son 1/3 , égale
24 ; égale 36 ; égale 80 ; égale 120.(indications :x +
1/3 x =24 =donc 4/3 du nombre =24) |
|
|
a) Ce nombre représente les 3/3
ajouté à son 1/3 = 24 ; donc 4/3
de ce nombre égal 24 Ce nombre vaut : 24 : ( 4/3) = ( 24
multiplié par 3 ) divisé par 4 =
18 b) Ce nombre représente les 3/3 ajouté à son 1/3
= 36 ; donc 4/3 de ce nombre égal
36 Ce nombre vaut : 36 : ( 4/3) = ( 36
multiplié par 3 ) divisé par 4 =
27 c) Ce nombre représente les 3/3 ajouté à son 1/3
= 80 ; donc 4/3 de ce nombre égal
80 Ce nombre vaut : 80 : ( 4/3) = ( 80
multiplié par 3 ) divisé par 4 =
60 d) Ce nombre représente les 3/3 ajouté à son 1/3
= 120; donc 4/3 de ce nombre égal 120 Ce nombre vaut : 120 : ( 4/3) = ( 120
multiplié par 3 ) divisé par 4 =
90 |
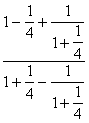
9 - Calculer :
|
A = |
|
|
Solution :
|
On pose : A = |
|
|
|
On calcule « B »=
|
|
|
|
On calcule «C » =
|
|
|
|
Donc « A » = |
|
|
|
A = |
|
|
|
A = |
|
|
|
1 |
I ) Un ouvrier
ferait un travail en 15 jours , un deuxième le ferait en 12 jours et un
troisième en 10 jours. S ‘ ils
travaillaient ensemble , quelle portion de l ’ ouvrage feraient - -
ils en 1 jour? |
|
|
Le premier fait 1/15 du travail en 1 jour le deuxième fait 1/12 du travail en 1 jour le troisième fait 1/10 du travail en i jours
|
|
2 |
Un bassin est alimenté par trois robinets : le
premier verse 50 litres en 6
minutes ; le deuxième 180 litres en 8 minutes , et le troisième 210 litres en 12 minutes. Combien ce
bassin reçoit - il d ‘ eau par minute
quand on ouvre les trois robinets en même temps ? * |
|
|
|
|
3 |
J ‘ avais droit au 4/5 d ’ une somme ( S ) ; on ne m ’ en donne que les 5 / 12 ;
combien me doit - on encore ? Quelle fraction de la somme totale m’ a t - on
remis ? |
|
|
Que représente ce calcul : 1 -
a) J’ai perçu les 5/12 des 4 /5 de la somme ; il me reste à
percevoir les 12/12 - 5 /12 = 7 /12 de
cette somme dû .Il me reste à toucher les 7/12 des 4/5 qui me reviennent. b) J’ai
perçu les : |
|
4 |
Deux ouvriers travaillant ensemble feraient un ouvrage en
20heures. Le premier ,seul, le ferait en 32
h .Quelle fraction de l ’ ouvrage ferait - il de plus que le deuxième
par heure ? (opérations
combinées) |
|
|
Seul le premier mettrait 12 heures
de plus que les deux ensembles soit les 12 / 20 de plus ou soit les 3/5 du temps en plus , s’il travaillait au même
rythme il ferait chacun 25/ 5 du
temps ; il travaille donc 5 / 50 fois plus que l’autre . |
|
5 |
Additionner 8 /15 ; 15 /21 ; 4 / 9 , et dire ce
qu ‘il faudrait ajouter au total pour avoir 3 entiers. |
|
|
On pose : On réduit tout au même dénominateur :
dénominateur commun = 15 fois 7 fois 9
= 945 :
|
|
6 |
Trois frères se partagent une somme : l ’ aîné en
prend les 4 / 9 et le second le tiers .Que reçoit le cadet ? |
|
|
On pose :
On transforme : On calcule : Conclusion : le cadet reçoit les 2 / 9
de la somme. |
|
7 |
Une fontaine donne par seconde 7 /15 de litre .Quel est le
débit par heure ? |
|
|
Le débit est de 60 fois 7 / 15 litre . Soit l’opération : |
|
8 |
Pour mettre en pièce
de vin en bouteilles , il a fallu 28 bouteilles de 3 / 4 de litre .Quelle est la contenance de cette pièce de vin ? |
|
|
Il faut faire le produit de 28 par les 3/4 . Soit La pièce de vin contient donc 21 litres. |
|
9 |
Un appareil de chauffage brûle 3/ 5 de litre de pétrole
par heure , combien en consomme - t -
il en 2 ; 3 ; 4 ;
5 heures. Quel doit être la capacité
minimale du réservoir pour chauffer 12 heures ? |
|
|
Les 3/5 représente le décimal : 0,6 En 2 heures il consomme : 1,2 litre En 3 heures il consomme : 1,8 litre En 4 heures il consomme : 2,4 litres En 5 heures il consomme : 3,0 litres Pour chauffer 12
heures sa capacité minimale sera de
12 fois 0,6 = 7,2 litres |
|
10 |
Un appareil de chauffage à un réservoir de 12
litres ; sa consommation est de 3 / 5 de litre de pétrole par heures.
Quelle est son autonomie ? |
|
|
Après avoir traité les deux problèmes précédents
on trouve facilement l’opération qu’il faudra faire : la division d’un nombre par une fraction. Sa capacité est de 12 / ( 3/5) = soit
20 ; son autonomie est de 20 heures |
|
11 |
Un adulte fait 17 inspirations par minute en introduisant
chaque fois les 5 / 9 d ‘ un
litre d ’ air dans ses poumons. Quel
est le volume d ‘air introduit en 24 heures ? |
|
|
Par heure = 60 minutes , dans
24 heures il y a : 60 fois
24 = 1440 mn Volume d’air inspiré : calcul : conclusion : le volume d’air inspiré est
de 13 600 litres . |
|
12 |
Un tisserand fait
14 /7 de mètre par heure , un autre en
fait 15 / 8 .Lequel des deux travaille le plus vite et combien fait - il de
mètres de plus que l’autre par journée e 10 heures ? |
|
|
Comparaison des deux fractions : (on réduit au même
dénominateur) Dénominateur commun : 56 Ouvrier 1
fait 14 / 7 =
112 / 56 m / h Et Ouvrier 2
fait 15 / 8 =
105 / 56 m /h L’ouvrier 1 fait
7 / 56 de m /h de plus soit :
en 10 h il fait 70 / 56 de m de plus que l’ouvrier 2 . |
|
13 |
Une mercière
possède une pièce ( rouleau) de ruban mesurant 36 m . Elle a vendu
le 1 / 4 de la pièce , puis
le 5/6 de la quantité restante
et le troisième client a acheté les 5
/9 qui restait de la pièce de
ruban .Ce ruban valant 5, 60 € le
mètre . 1°) Quelle somme a - t - elle reçue ? 2°)Quelle fraction du rouleau lui reste - il ? |
|
|
1°) Calcul de la somme reçue : a) Quantité vendue exprimée en fraction :
b) Elle
a en suite vendu les
5 / 6 des ( 36 - 9 =)
27 m de ruban restant. Soit ( 27
fois 5 ) / 6 = 22 , 5 m
pour la somme de 22,5 fois 5,60
= 126 € c) Elle a
en suite vendu les 5 / 9 de
(27 - 22,5 =) 4,5 m soit 2,5 m
à 5,60 = 14 € d) elle a reçue la somme de : 50,4
+ 126 + 14 = 190 ,4 euros. 2°) a) Si
elle avait tout vendu elle aurait reçue
: 36 fois 5,6 soit = 201,6 € b) somme non perçue : 201,6 - 190 , 4 = 11,2 ; les
11,2 / 201,6
représente en fraction la quantité non vendue
vérifions : 1 / 18 de 36 m = reste 2
m à 5,60 soit 11,2 € cela correspond à la somme non perçu . Il
lui reste donc 2 m de ruban à vendre. |
|
14 |
Je voudrais acheter un meuble de 1800 €. .Je ne dispose que des 5 /7 de
1470 €. Combien me manque - t - il ? |
|
|
Il me manque : 1800
- (1470 fois 5) divisé par 7 =
1800 - 1050 = 750 € |
|
15 |
Les 2 /5 d ‘ une
perche de 4,80 m sont peints en blanc ; 1/3 en rouge et le reste en
bleu. Quelle est la longueur de la partie peinte en bleu ? |
|
|
Longueur peinte en blanc et rouge : 4,80 ( On additionne les fractions ( dénominateur commun : 15 ) : 6 / 15 + 5 / 15 = 11/15 Il reste à peindre les 15 / 15
- 11 / 15 = 6 / 15 en bleu. |
|
16 |
Un champ de 4 / 5 d ‘hectare a été partagé en 12 parcelles égales .Quelle est la surface de
chaque part ? |
|
|
Un hectare = 10 000 m² Calcul :
La superficie de chaque parcelle est de 667
m² |
|
17 |
On a tiré 135
litres de vin d ‘un tonneau de 225 litres. Combien faut - il de bouteilles
de 3 /4 de litre pour contenir le vin qui reste
dans le tonneau ? |
|
|
Deux solutions pour parvenir au résultat : 1°)
solution : on calcule le nombre de bouteilles
« tirées » : 135 / ( 3 /4) = …180. On calcule le nombre de bouteilles que l’on
pourrait tiré : 225 : ( 3/4)
= …300.. On fait une soustraction : 300 - 180 = 120 2°) on
calcule ce qui reste à tirer en litre : 225 - 135 = 90 litres On calcule le nombre de bouteilles que cela
représente : 90 : ( 3/4)
= 120 bouteilles. |
|
18 |
Un appareil de chauffage
dépense 710 litres de gaz en 7 h ½
, un autre dépense 640 l en 5h
½ .Quel est celui qui en dépense
le plus , et combien par heure ? |
|
|
C’est un problème de comparaison : On sait
½ = 0,5 On pose 710 litres de gaz en 7,5 h et un autre
dépense 640 l en 5,5 h On
peut calculer avec les nombres décimaux On calcule : 710 / 7,5 =
94 , 66666 et 640 / 5,5 = 116, 3636 Celui qui dépense le plus est le second ;
la différence est de 116,3636 - 94,666= …. On peut calculer avec les fractions : On compare
( 7100 / 75 ) et ( 6400 / 55 ) ; on réduit au même
dénominateur !!! On rend irréductible les fractions : ( 7100 / 75 ) devient
(284 / 3) et et
( 6400 / 55 ) devient : (1280 / 11) ; le dénominateur
commun est : « 33 » - (284 /
3) devient : 3 124 / 33 et
( 1280 / 11
) devient : (3 840 / 33) On constate que le second consomme plus. On calculera alors : ( 6400 / 55 ) - (
7100 / 75 ) = ; on utilise les
fractions ci dessus :
Soit 3 840 / 33 -
3 124 / 33 = 716 / 33 |
|
Série : Problèmes de la vie courante : fraction
d’un nombre |
|
19 |
Une ménagère va au marché avec 150 Euros, elle dépense les 2/3 de cette somme
.Combien lui reste - t - il ? |
|
|
Il lui reste
3/3 - 2/3 = 1/3 En valeur il lui reste 150 ( 1/3)
= 50 € |
|
20 |
On a soutiré 105 litres de cidre d ‘ un tonneau et il en
reste encore les 2 /5 .Combien de litres contenait - il ? |
|
|
105 litres représentent les ( 5/5 ) - ( 2 / 5 ) = (
3 / 5 ) du tonneau La capacité du tonneau est donc de :
105 : ( 3/5) = 175 Le tonneau contenait : 175 litres. |
|
21 |
Un marchand a vendu 63 mètres de drap, il lui en reste
encore les 2 /5 , combien de mètres avait - il ? |
|
|
63
mètres représentent les ( 5/5 )
- ( 2 / 5 ) = ( 3 / 5 )
vendus Il avait à vendre: 63 : ( 3/5) = 105
Il avait
105 mètres |
Fraction de fraction.
|
22 |
Le lait donne en moyenne 1 / 6 de sa masse en crème , et
celle-ci donne environ ¼ de sa masse en beurre. Combien de beurre
obtiendra - t - on avec 2000 litres de lait si le litre pèse 1,030 kg ? |
|
|
Masse de lait : 2000 fois 1,030 =
2060 kg On obtient
(1/4 ) des (1/6) de lait :
soit l’opération :
|
|
23 |
Un agriculteur a recueilli 300 quintaux de noix , quelle
quantité d ’ huile pourra - t - il en
tirer si les 3/5 de la masse de la noix se perdent en coque et bois ; et
que les amandes donnent les 3/7 de leur masse en huile ?. |
|
|
1°) il récolte les 5/5 - 3/5 = 2/5 d’amandes soit 30 000 kg fois 2/5 = 12000 kg d’amandes 2°) Quantité d’huile : les 3/7 de 12 000 = 5 142,857 kg d ‘huile. |
|
24 |
les ¾ de mes
économies égalent 1 560 francs. Combien ai - je économisé ? |
|
|
indications : ¼ de mes économie
représente : 1560/3 = 520 ; la totalité de mes économies (4 quarts égale 520 |
|
25 |
Une personne achète une propriété et en paye les 3/7 en
donnant 18 585 euros. Quelle est la valeur de cette propriété ? |
|
|
Calcul :
18 585 : ( 3/7) =
43 365 € |
|
26 |
Julie a 16 ans
½ ,et son âge est le 3/5 de celui de
Louis. Quel est l ‘ âge de ce dernier ? |
|
|
Calcul :
16,5 : ( 3/5) = (16,5 fois 5) / 3
= 27 , 5 ans |
|
27 |
Pour payer 7,50 m d’ étoffe à 1 3 8 Euros le mètre une personne a donné les
¾ de ce qu’ elle avait dans sa bourse.
Quelle somme avait - elle ? |
|
|
Les trois quart
représentent : 138 fois 7,5 =
1035 € La somme
qu’elle possédait était de : (1035 fois 4) / 3
= 1380 € (à vérifier) |
|
28 |
Les 3/5 d’un nombre valent 27 ; les ¾ d’un autre
valent 21 .Quelle est la somme de ces deux nombres ? |
|
|
Les 5 / 5 de 27 sont : 27 : ( 3/5) = (27 fois 5 ) : 3 = 45 Les 4/4 de 2& sont :
21 : ( 3/4) = ( 21 fois 4
) : 3 = 28 La somme des deux nombres est donc de : 45
+ 28 = 73 |
|
29 |
Les 2/5 d ’ une
succession ont été partagés entre 4
héritiers , chacun a reçu 45 000 euros .Quel est le montant de l ’
héritage ? |
|
|
Les 2/5 de l’héritage représente la somme de 45 000 fois 4 = 180 000 € Le montant de l’héritage est de 180 000 : ( 2 /5) =
180 000 fois 5 divisé par 2 =
450 000 € |
|
30 |
En faisant 4,200 km à l ’ heure , j’ai mis 3 heures pour
parcourir les 5/9 de la distance qui sépare 2 villes .Quelle est cette distance ? |
|
|
Distance parcourue en 3 h : 4,2 fois 3 = 12,6 km Cette distance représente les 5/9 de la distance
qui sépare les deux villes : La distance qui sépare ces deux villes est
obtenue en faisant le calcul suivant :
12,6 : ( 5 / 9) = (12,6
fois 9) divisé par 5 = 113,4 : 5
= 22 , 680 km |
|
31 |
Une somme a été partagée entre 3 héritiers .Le premier a
eu les 2/7 de la somme , le deuxième les 3/5 et le troisième le reste .Trouver le part de
chacun des héritiers , sachant que le premier a reçu 84 500 Euros. |
|
|
a) On
sait que 84 500 représente les 2/7 de l’héritage : l’héritage est
donc de : 84
5 000 : ( 2/7 ) =
(84 500 fois 7) divisé par 2
= 295 750 € l’héritage est de 295 750 € b) le second à reçu : les 3 /5 de 295 750 : soit
(297 750 fois 3) divisé par 5 =177 450 la somme perçue
par les deux premiers est de
84 500 + 177 450 = 261 950 € c) le troisième à reçu : 295 750 -
261 950 = 33 800 € d)
vérification : soit « x » la fraction
d’héritage perçu par le troisième.
2 / 7 + 3 / 5 + x = 1 soit
10 /35 + 21 /35 + x = 35 /35 on en
déduit que x = 4 / 35 et les 4 / 35 de 295 750 =
33 800 , ce qui vérifie que les calculs précédents sont bons. |
|
32 |
On demandait à un homme
son âge et celui de sa femme .Il répondit : les 3/8 de mon âge
font 15 ans , et l ‘âge de ma femme est le
¾ du mien. Calculez, d ‘après cela , les deux âges. |
|
|
L’âge de l’homme : 15 / (3/8 ) =
(15 fois 8) divisé par 3 = 40
ans L’âge de sa femme est : 40
fois ( 3/4) = 120 / 4 = 30 ans |
|
33 |
Une personne a vendu les 2/3 des ¾ de son stock de
cassettes vidéo pour 675euros , à
raison de 7,50 euros la cassette
.Combien avait - elle de cassettes en
stock ? |
|
|
Nombre de cassettes vendues : 675 :
7,5 = 90 ; soit 90
cassettes ; Les 2/3 des 3/4 représente en fraction les 90 cassettes : soit 2/3 fois 3/4 =
6/12 soit 1/2 . Les 90 cassettes représente la moitié du stock .
soit 90 : ( 1/2) = 90 fois 2 Le nombre de cassettes en stock était donc
de 90 fois 2 = 180 cassettes. Vérification : les 3/4 de 180 = 135 ; les 2/3 de 135 = 90 ce qui vérifie que 180 est bien le
nombre recherché. |
|
34 |
Pendant une première année , une personne augmente son
nouvel avoir des 2/7. L ‘ année suivante , elle augmente son nouvel avoir des
2/7 et possède alors 41 013 euros .
Trouver son avoir primitif. |
|
|
Avoir avant la deuxième augmentation ;
elle avait 7/7 et elle l’augmente
cette somme de 2/7 , ainsi les
41 013 représente les 9/7 de la somme précédente : Calcul de la somme précédente est donc
de 41 013 : ( 9/7) = (41013
fois 7) divisé par 9 = 31 899 € Calcul de son avoir primitif : on
recommence le même raisonnement et on calcule les 31 899 : ( 9 /7)
= (31 899 fois 7 ) : 9 = 24 810,33 |
|
35 |
Un négociant avait acheté les ¾ d ’ une pièce de tissu au
prix de 30 euros le mètre. Il vend les 2/3 de cet achat pour 6 60 € en faisant un bénéfice de 60 € dans cette
vente. Trouver la longueur de la pièce |
|
|
Prix d’achat des 2/3 de la pièce de tissus :
660 - 60 = 600 € Ces 2/3
représente une longueur de
600 : 30 = 20 m La longueur
acheté est de 20 : (
2/3) =
(20 fois 3 ) divisé par 2 = 30
m Puis que les 30 m représente les 3/4 de la pièce
complète ; la longueur de la pièce totale est donc de 30 : ( 3/4) soit
( 30 fois 4) divisé par 3 = 40
m |
.
|
36 |
Si mon avoir était
augmenté de son ¼ , j ‘ aurais 550 Euros. Combien ai - je ? |
|
|
550 € représente la somme de 4/4 + 1/4 = 5/4 J’ai avant l’augmentation : 550 : ( 5/4) = (550 fois 4) divisé par 5 = 440 € |
|
37 |
Une ville compte 8
000 h. Combien en comptait - elle il y a 10 ans , sachant que pendant cette
période sa population s ‘est accrue de ses
1/ 15 ? |
|
|
Les 16 /15 de la population représente :
8000 La population était de 7 500 h. |
|
|
LES
ENONCES suivants FONT APPELLENT A D’ AUTRES CONNAISSANCES ( l’égalité de deux fractions ; les
proportions ….) |
|
|
|
|
38 |
Sachant que 16 m de
tissu ont été payés 720 € ,trouvez le prix de 28m |
|
|
Résolution : Le prix étant proportionnel à la longueur , le prix cherché est :
au lieu d'utiliser les fractions , on peut
employer la méthode de "réduction à l'unité". Le prix du mètre de
tissu est de Le prix de 28 m est de 45 |
|
39 |
Sachant que pour
faire un gâteau de 4 personnes six œufs ,combien faut-il d'œufs pour faire un
gâteau de 6 personnes ? |
|
|
Résolution
: Le nombre d'œufs étant proportionnel au nombres de
personnes , le prix nombre d'œufs
cherché est :
Explication du calcul:
Au lieu
d'utiliser les fractions , on peut employer la méthode de "réduction à
l'unité". Le nombre d'œufs par personne est de Le nombre d'œufs pour 6
personnes est de 1,5 A propos des
unitésL qui s' annulent par la
division: les unités de même "famille" s ' 'annulent dans la division: exemple:
soit : |
|
40 |
Un entrepreneur
fait construire d ' habitude
une maison en 60 jours avec 15
ouvriers .six personnes tombent
malades, déterminer la durée des travaux . Remarque : Il n ' y a pas de proportionnalité : le
travail de l'ensemble des personnes ne peut se réduire au travail d'un
seul individu . |
|
|
La durée des travaux étant proportionnel aux
nombres de personnes , la durée cherchée est : Le nombre de jours est
constant : 60 Il y a
15 - 6 = 9 ouvriers
pour effectuer les 900 jours de travail Conclusion:
900 : 9 =100 ; il faudra 100 jours pour construire la
maison |
|
41 |
18 ouvriers ont fait
, dans des conditions déterminées , 60 mètres d'ouvrage. Combien 30
ouvriers feraient-ils de mètres du même ouvrage, toutes les autres conditions
restant les mêmes ? |
|
|
Résolution : Les deux grandeurs sont directement proportionnelles . Le nombre de mètres construit
étant proportionnel au nombres de personnes , le nombre de mètres cherchés
est : Explication du calcul:
Au lieu d'utiliser les fractions
, on peut employer la méthode de "réduction à l'unité". Le nombre
de mètre par personne est de Le
nombre de mètres pour 30 personnes est
de 10/3 A propos des unitésL qui s'
annulent par la division: les unités
de même "famille" s '
'annulent dans la division: exemple:
soit : |
|
42 |
Une pompe remplit un
réservoir en 3 h , une deuxième pompe remplit le réservoir précédent en 5 h .Si les deux pompes fonctionnent ensemble ; quelle
fraction du réservoir remplissent – elles
en 1 h ? Quel temps mettent – elles pour remplir le réservoir. ? |
|
|
Réponse : en 1 heure elles remplissent 1/3
+ 1/5 du bassin soit 5/15 +3/15 = 8/15 du bassin ( 1
heure = 60 minutes ) Temps pour remplir le bassin avec les deux
pompes : 60 : 8/15 = 60 x 15 :8 =112,5 min |
|
43 |
J’ achète une
bicyclette 1300 €, je verse 1/10 du
prix à la commande et 3/5 à la livraison .Quelle fraction du prix total me reste-il à payer ? Quelle somme cela représente
–il ? |
|
|
Réponse : Fraction du prix total
payé : 1/10+3/5 = 1/10+6/10 =
7/10
Les 7/10 représente la somme de : (1300
fois 7 )/10 = 910 € |
|
44 |
Une vis avance de ¾
mm par tour ; de combien avance
t-elle en 10 tours ;en 12 tours ; en
28 tours ; en 40 tours ? |
|
|
|
|
En 10 tours
, elle avance de |
¾ fois 10 = 30/4
= 7,5 mm |
|
En 12
tours elle avance de |
¾ fois 12
= 36 / 4 = 9 mm |
|
En 28 tours
, elle avance de |
¾ mm 28 = 54 / 4 = 71 mm |
|
En 40 tours
, elle avance de |
¾ mm 40 = 120 / 4 = 30 mm |