Niveau V - LECON N°16	Devoir : Ÿ Remédiation : Ÿ	Nom :…………	Classe : Groupe :
Date :……………	Rattrapage : Ÿ Soutien : Ÿ	Prénom :…………	Note contrôle :	Note évaluation :

DEVOIR type N°16 sur : LES SYMETRIES

CORRIGE :

CONTROLE:

1°) Nommer 2 droites qui sont "axe de symétrie" .précisez ?

2°) Compléter les phrases suivantes :

Par une symétrie centrale de …………. "O" :

- l'image d'un segment est ………………………………………. .

- l'image d'un angle est …………………………….. .

- l'image d'un polygone est ……………………………………...

- L'image d'un cercle est ……………………………………….. .

La symétrie centrale conserve ………………………………….. .

3°) Compléter les phrases suivantes :

Par une symétrie orthogonale ……………. ( D ) :

- l'image d'un segment est ……………………………………… .

- l'image d'un angle est un ……………………………………… .

- l'image d'un polygone est ……………………………………….

- L'image d'un cercle est ………………………………………… .

La symétrie orthogonale conserve ……………………………….. .

EVALUATION:

A) Symétrie centrale :

1°) construire le symétrique de M par rapport à "O"

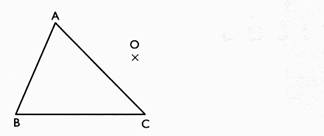
2°) construire le symétrique du segment AB par rapport à "O"

3°) Construire le symétrique de l'angle par rapport à "O"

4°) construire le symétrique du polygone ( triangle) par rapport à "O"

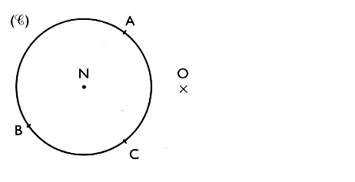
5°) construire le symétrique du cercle par rapport à "O"

6°) tracer un segment [ A B ] de 7 cm de longueur et placer un point O à une distance de 4 cm de la droite ( AB ) . Construire le symétrique [ A' B' ] du segment AB par rapport à O . vérifier que le symétrique du milieu "N" du segment AB est le milieu N' de [ A' B '] . On dit que la symétrie centrale conserve le milieu .

7°)

Dessiner avec la règle et le compas la symétrie de la figure ci-contre de centre S .

B ) Symétrie orthogonale :

1°) Construire le symétrique orthogonal du point M , N et P .

2°) Construire le symétrique orthogonale du segment AB , par rapport à la droite ( D ) .

3°) Construire le symétrique orthogonale du segment AB , par rapport à la droite ( D ) .

3° ) Construire le symétrique orthogonale du segment AB , par rapport à la droite ( D ) .

4°)Construire les symétriques des droites ( d ₁ ) et ( d₂ ) parallèles par rapport à la droite ( D) .

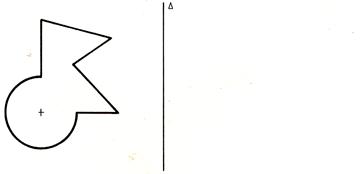
5°) Dessiner la figure ci-dessous dans la symétrie orthogonale d’axe  « delta » . Pour cela il faut déterminer l’image de certains points .

Laisser les droites perpendiculaires à « delta » apparentes

6°) xx’ et yy’ sont deux droites perpendiculaires sécantes en « O ».Dessiner l’image F’ de la figure « F » dans la symétrie orthogonale d’axe x’x puis l’image « F’’ » de la figure « F’ » dans la symétrie orthogonale d’axe yy’ .