CORRIGE DES EXERCICES DU COURS
+Exercice n°1
|
x |
12 |
15,5 |
-8 |
3,14 |
87 |
100000 |
3669,778 |
1475 |
0 |
|
Ln x |
2,485 |
2,741 |
Non défini |
1,144 |
4,466 |
11,513 |
8,208 |
7,296 |
Non défini |
+Exercice n°2
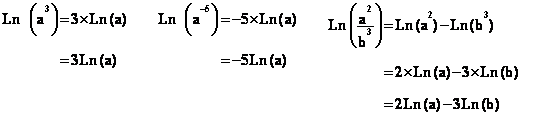
![]()
+Exercice n°3

![]()
+Exercice n°4
|
x |
102 |
10-5 |
108 |
10-5,7 |
10-12,7 |
1099 |
10-37,5 |
103 |
101 |
|
Log x |
2 |
-5 |
8 |
-5,7 |
-12,7 |
99 |
-37,5 |
3 |
1 |
On
utilise la propriété : Log(10x) = x.
+Exercice n°5
1°)
En appliquant la formule : C4 = 2500´(1+0,05)4 =
3038, 77 (arrondi à 0,01)
2°)
La première étape consiste à remplacer dans la relation donnée les grandeurs
que l'on connaît :
A
savoir C = 2 500 € t = 0,05 Cn
= 4 275,85 €
La
relation devient avec ces valeurs :
4 275,85 =2 500 ( 1 + 0,05 )n
4 275,85 = 2 500 ´ 1,05n
On
veut déterminer la valeur de n, il faut donc dans un premier temps isoler dans
le membre de droite 1,05n en divisant les deux membres l'équation
par 2 500 :

C'est
à partir de cette équation que l'on va se servir des propriétés opératoires des
fonctions logarithmes.
On
prend le logarithme décimal ( ou népérien peut importe
car elles ont les mêmes propriétés opératoires) des deux membres :
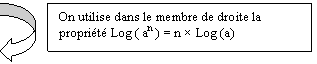
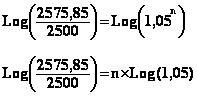
On
peut maintenant diviser les deux membres de l'équation par Log(1,05)
afin d'isoler n et d'en déterminer ainsi la valeur.
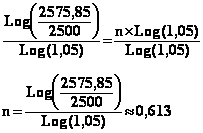
Il
faut donc environ 0,613 années soit 7 mois et 11 jours environs.
+Exercice n°6
|
x |
-3,5 |
8 |
-1/2 |
3/4 |
6 |
0 |
|
ex |
0,030 |
2980,958 |
0,607 |
2,117 |
403,429 |
1 |
+Exercice n°7