Probabilités.
La problématique.
Dans
le programme des baccalauréats professionnel, le paragraphe consacré aux probabilités
est assez bref, comme nous pouvons le voir ci-dessous :
VIII. Initiation aux probabilités.
Au collège et au cycle B.E.P., les élèves ont étudié la description de séries statistiques
à une variable.
Pour le baccalauréat professionnel, les probabilités sont une nouveauté et
doivent être considérées comme une initiation aux phénomènes aléatoires.
L'objectif est de décrire quelques expériences aléatoires simples et de se
familiariser avec la notion de variable aléatoire. Toute théorie formalisée et
toute technicité exagérée sont exclues.
Le contexte professionnel fournit un large éventail des situations mettant en
jeu des phénomènes aléatoires.
Il est important que les élèves puissent se familiariser avec les probabilités
pendant une durée suffisante, répartie sur les deux années de formation.
a) Vocabulaire des probabilités.
|
A partir d'expériences aléatoires simples, notion d'événement, d'événement élémentaire, d'événements incompatibles. |
Pour introduire la probabilité d'un événement, on peut s'appuyer sur l'étude des séries statistiques obtenues par répétition d'une expérience aléatoire, en soulignant les propriétés des fréquences et la relative stabilité de la fréquence d'un événement lorsque cette expérience est répétée un grand nombre de fois. La notion de probabilité conditionnelle n'est pas au programme. |
b)
Variable aléatoire.
|
A partir d'expériences aléatoires simples issues du domaine professionnel, notion de variable aléatoire. Interprétation de l'espérance, de l'écart-type et de la densité. |
|
Champ des activités.
|
Exemples simples d'emploi de partitions et de représentations ( arbres, tableaux, urnes ... ) pour organiser et dénombrer des données relatives à la description d'une expérience aléatoire. |
On se limite à des exemples simples permettant de mettre en valeur les concepts, mais ne comportant pas de difficultés combinatoires. |
|
Exemples simples d'étude de situations de probabilités issues d'expériences aléatoires. Exemples d'étude de situations conduisant à l'utilisation d'une variable aléatoire associée à une loi normale. |
Toutes les indications nécessaires doivent être données sur la méthode à suivre. Aucune connaissance n'est exigible concernant la loi normale en mathématiques. |
Nous prenons ici le parti de limiter notre exposé à un seul objectif, à savoir montrer qu'un modèle mathématique, celui de la loi normale,
permet de simplifier une recherche de rendement dans une production.
Pour cela nous faisons d'abord découvrir le vocabulaire des probabilités en
général et des probabilités à densité en particulier.
Dès le paragraphe IV ( page 6 )
la problématique du théorème de la limite centrale apparaît et fait pressentir
l'intérêt des lois normales.
En conclusion, l'exercice du paragraphe VI ( page
8 ) met en scène la problématique proposée en développant un cas qui
pourrait fort bien exister quelque part en France.
Les prérequis.
Pour
éviter toute confusion des genres, nous postulons que
·
Les méthodes du
calcul statistique sont parfaitement maîtrisées depuis la classe de B.E.P.
·
La
combinatorique, dont l'intérêt se limite aux seuls évènements équirépartis, a été traitée.
On peut penser que ce dernier point, comme le traitement des arborescences, n'a
que peu d'intérêt tant qu'on ne parle pas des probabilités conditionnelles,
hors programme.
Plus qu'une leçon type qui n'aurait que peu de signification, ce dossier
propose quelques documents pouvant être utilisés dans différents contextes
pédagogiques.
L'ensemble du dossier proposé contient :
·
Un document élève
complet, « probab_f.pdf »
comprenant huit pages de cours interactif dont deux pages d'exercices.
·
Le même document
en version blanche, « probab_w.pdf »,
laisse des trous pour les réponses des élèves.
·
Les fichiers
sources des documents présentés. Ces fichiers sont fournis au format Latex,
pour le texte, et PostScript ( eps ),
pour les graphiques.
Comme toujours, tous les fichiers sont totalement libres à la copie et à
l'utilisation.
I. Probabilité d'un évènement ( page
1 ).
Nous
utilisons les notions intuitives sous jacentes pour préciser le vocabulaire des
probabilités.
L'équiprobabilité est omniprésente sans être théorisée. Il faudra
attendre le paragraphe IV pour remettre en cause cette omniprésence.
Attention.
Il
incombe à l'intervenant de s'assurer que la terminologie employée est
parfaitement comprise de son auditoire, car peu de termes sont explicitement
définis dans le document écrit.
Cette option, qui vise à alléger le support papier d'une partie de la théorie,
exige une plus grande implication du discours oral. Avec certaines classes, un
débat ouvert peut être envisagé.
A la fin du paragraphe I, les élèves devraient avoir retenu qu'un évènement est
un ensemble, peut être un ensemble de cas favorables, et que la probabilité est
une mesure de cet ensemble.
Le terme d'évènement élémentaire, plus ambigu, n'apparaît que dans le
paragraphe suivant.
II. Variable aléatoire ( page
2 ).
L'étude
des variables aléatoires reprend le travail effectué sur les fréquences en
statistique.
Ici encore, nous proposons que la pratique précède la théorie.
Bien encadrées, les activités 3 et 4 ne doivent pas poser de problème majeur.
Le cas échéant une analogie ( densité
linéique ) avec la mécanique ou avec l'électrostatique peut être tentée.
Attention.
Pour
la fonction de répartition, nous avons choisi de prendre la probabilité de
l'intervalle ![]() ouvert
en
ouvert
en ![]() ,
d'autres auteurs préfèrent le fermer.
,
d'autres auteurs préfèrent le fermer.
Ce point ne mérite pas de faire l'objet d'un débat et peut passer inaperçu de
l'auditoire.
Par contre, on sera amené à préciser d'une façon ou d'une autre, et lorsque la
question se posera, que pour une variable aléatoire continue les
intervalles ouvert et fermé ont même probabilité.
Ou, autrement dit, que pour une variable aléatoire continue la
probabilité d'une valeur isolée est toujours nulle.
II-1. Détermination de la loi de probabilité
d'une variable aléatoire.
Le
paragraphe II-1 ( page 3 )
marque un tournant dans le développement de notre problématique : Une loi
de probabilité n'a que peu à voir avec une suite de mesures statistiques mais
est un modèle mathématique défini par un mathématicien.
L'usage de ce modèle et non le modèle lui-même peut ensuite être validé
pour une application donnée.
On demandera à nos élèves de vérifier qu'une machine suit une loi normale
avant d'exploiter les résultats liés à ce modèle.
Notons que l'exemple de l'activité 5 est choisi pour la simplicité du calcul.
Cet exemple est présenté page 3 pour introduire l'exercice 1 ( page
4 ). Le même exemple est repris, page 5, pour le calcul approché de
l'espérance et de la variance. La loi normale proposée n'est pas une loi
normale réduite dont l'intérêt ici ne serait pas flagrant.
Dans cet exemple, et selon la méthode développée en statistique, les valeurs
« continues » sont groupées par classes.
Chaque classe est affectée d'une probabilité produit de la valeur centrale de
la densité par l'amplitude de la classe.
Ici encore, on évitera toute polémique sur les intervalles ouverts ou fermés.
Le document complet propose la fonction de répartition obtenue par intégration
de la densité.
On peut s'attendre à ce que les élèves proposent plutôt un premier résultat qui
aura l'allure suivante :
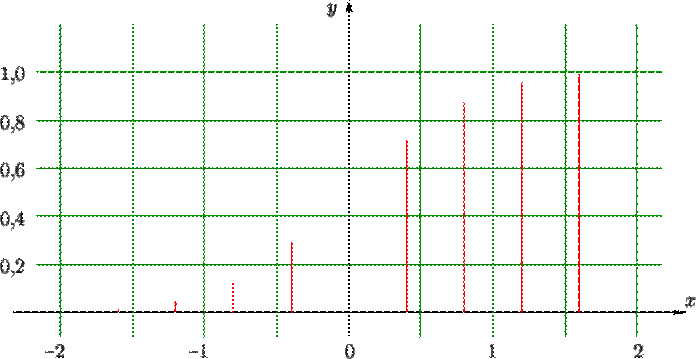
On
leur suggère alors de joindre les points obtenus pour obtenir un résultat
analogue au polygone des fréquences cumulées croissantes en
statistiques, ou mieux, de lisser la courbe.
III. Espérance mathématique, écart-type ( page 5 ).
Les
définitions et les calculs sont calqués sur leurs homologues en statistique.
On notera la préférence donnée à l'expression espérance mathématique par
rapport à la moyenne utilisée en statistique.
L'activité 6 reprend quasiment mot pour mot les méthodes de calcul utilisées
dans le cours de statistiques de BEP, ces méthodes ne sont pas rappelées ici
mais peuvent faire l'objet d'une remise au point en classe.
Les calculs, menés à la machine ne posent pas de problème.
Dans l'activité 7, on soulignera combien le résultat obtenu est une valeur
approchée de la valeur exacte qui existe et que seul un calcul
d'intégrales peut déterminer.
IV. Loi uniforme et loi normale ( page
6 ).
Le
paragraphe IV marque le deuxième tournant dans le développement de notre
problématique en faisant découvrir l'intérêt des lois normales.
Pour ce faire, l'activité 8 est explicite.
La lecture du diagramme représentant les positions des dés permet de construire
immédiatement la loi de la somme ![]() .
.
Pour trois dés le dénombrement est plus ardu, nous suggérons que l'enseignant
le laisse de côté et fournisse directement les résultats du diagramme II.
Notons que nous laissons les auditeurs faire la confusion entre une
« limite de loi discrète » et une loi continue car, si l'intérêt des
lois discrètes portant sur des univers finis est plus que limité, le calcul sur
un nombre fini de classes permet une compréhension significative des lois
continues sans utiliser les outils du calcul intégral.
Exemple ( page
7 ).
Dans
le même esprit, nous proposons les résultats d'un exemple simple à
comprendre : On imagine une chaîne mécanique réalisée de façon à laisser
un jeu de plus ou moins un millimètre entre deux éléments successifs.
Pour quatre éléments, le jeu sur trois liaisons peut varier entre plus ou moins
trois millimètres mais on pressent qu'il a plus de chance de se trouver au
centre plutôt que « sur les bords » de cet intervalle.
Les parenthèses suivantes ne concernent pas forcément nos élèves.
(i)
Dans
l'exemple de la page
On part de la densité uniforme sur ![]()
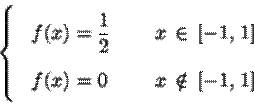 .
.
On
en en déduit :
![]() ,
soit,
,
soit, 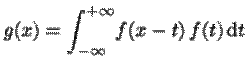
Cela
donne explicitement :
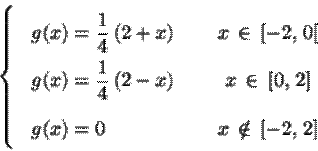
On
reprend la méthode pour déterminer, ![]() ,
soit :
,
soit :
(ii)
Le
paradoxe de Lucky Luke, ou le vice des lois uniformes.
Chacun sait que la probabilité de recevoir une balle est proportionnelle à
l'aire de la surface exposée ( équiprobabilité ).
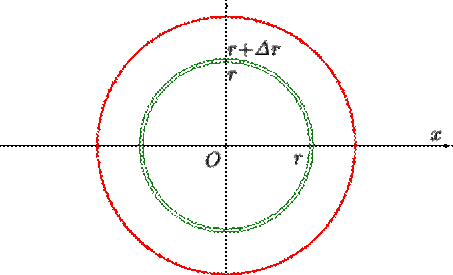
Considérons donc une couronne circulaire de centre ![]() ,
de rayon
,
de rayon ![]() et
d'épaisseur
et
d'épaisseur ![]() ,
la probabilité de toucher cette couronne est proportionnelle à
,
la probabilité de toucher cette couronne est proportionnelle à ![]() .
.
Si maintenant nous considérons une cible circulaire de centre ![]() et
de rayon
et
de rayon ![]() sur
laquelle nous traçons un axe
sur
laquelle nous traçons un axe ![]() la
probabilité de toucher une couronne passant par le point
la
probabilité de toucher une couronne passant par le point ![]() d'abscisse
d'abscisse
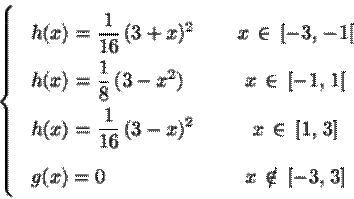
![]() suit
une loi de densité :
suit
une loi de densité :
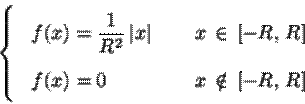
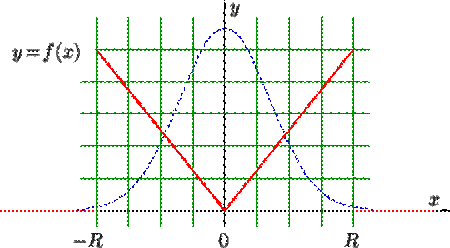
En fait, cette loi est plus précisément la loi conditionnelle « sachant
que la cible est atteinte », l'évènement ne pas toucher la cible étant ( presque ) certain.
Voir en référence : L'école des shérifs, dans « La ballade des
Dalton », Dargaud éditeur.
On peut être tenté de modéliser le problème par d'autres lois uniformes, sur
une sphère dont le centre est le tireur, dans un cône astucieusement choisi
etc. mais la conclusion naturelle, nous n'osons pas dire normale, est que la
loi de densité en ![]() se
rapproche d'une gaussienne plus ou moins évasée selon la qualité du tireur.
se
rapproche d'une gaussienne plus ou moins évasée selon la qualité du tireur.
Pour Lucky Luke, ce serait une distribution de Dirac, mais cela ne nous
concerne pas.
Les parenthèses refermées, nous reprenons notre cours au niveau du bac pro.
Nous suggérons de présenter rapidement le diagramme proposé en haut de la page
7 pour faire comprendre que la nature exacte de la loi de départ n'est pas
importante, mais que les effets conjugués d'un grand nombre de variables, discrètes
ou continues finissent par donner un résultat « assez régulier ».
Un corollaire de ce principe est que, si l'étude d'une machine donne des
résultats trop irréguliers, alors la machine présente un défaut grave dans sa
structure même.
Soulignons encore que l'hypothèse de départ, à savoir que la position d'un
élément de la chaîne mécanique suit une loi uniforme sur son intervalle de jeu,
n'a pas d'importance, le tout est que tous les éléments de la chaîne suivent à
peu près la même loi.
Le nombre des variables prises en compte n'est, en général, pas critique. Comme
nous le voyons, la forme en cloche apparaît dès le troisième élément.
Attention.
Il
importe que l'enseignant développe ici les principes de l'utilisation
des lois normales lors de l'évaluation d'une chaîne de production et fournisse
aux élèves les méthodes nécessaires à la résolution de l'exercice
d'application du paragraphe VI.
Le paragraphe V complète cette étude en fournissant quelques valeurs numériques
nécessaires à l'exploitation pratiquedu modèle
gaussien.
V. Propriétés des loi normales ( page
7 ).
Conformément
au programme, on ne s'attache pas à la définition de la gaussienne.
Dans les commentaires il peut être utile d'insister sur la symétrie d'une
courbe en cloche et sur son comportement à l'infini.
Le point clef du paragraphe V est le fait que les formules « d'encadrement
de l'erreur » proposées ne sont valables que pour une loi « proche
d'une loi normale ».
Quand c'est la cas, les énoncés du baccalauréat professionnel
ne manquent pas de rappeler que la loi considérée peut être assimilée à une loi
normale.
Les deux formules qui fixent les barres des 95 % et des 99 % et
figurent dans ce paragraphe font partie du formulaire du Bac Pro, elles n'ont
pas à être apprises par coeur, pas plus d'ailleurs, que la formule de la
densité d'une loi normale.
Dans l'exercice 2 du paragraphe suivant, nous faisons figurer ces barres, de
façon discrète sur les diagrammes proposés aux élèves.
VI. Exercice d'application ( page
8 ).
On
propose l'étude de trois cas caractéristiques :
·
Une loi normale
décalée par rapport à la consigne, mais dont la dispersion est presque
acceptable.
·
Une loi normale
correctement centrée mais de dispersion rédhibitoire.
·
Une loi qui n'a
rien d'une loi normale et pour laquelle on ne peut pas appliquer les
formules.
N.B.
Rappelons
au passage qu'il est facile de créer des densités aux formes exotiques en
multipliant une fonction ![]() par
un polynôme qui reste positif sur
par
un polynôme qui reste positif sur ![]() .
.
Les élèves sont invités à commenter les graphiques et les valeurs fournis.
Pour les calculs il est hors de question de demander plus qu'un ordre de
grandeur.
En conclusion.
Nous
avons pris le parti de favoriser l'appréhension de lois continues non uniformes
au dépens des lois discrètes issues de la conjonction
de la combinatorique et du principe d'équiprobabilité.
De l'analyse statistique, nous avons exploité les méthodes mais nous refusons
de présenter une loi de probabilité comme un avatar d'une accumulation de
statistiques plus ou moins convergentes.
Les statistiques sont un moyen de voir, ou de ne pas voir, une certaine réalité
physique, alors que les probabilités restent un modèle mathématique.
Il nous paraît primordial que des élèves de l'enseignement professionnel
prennent conscience de l'existences des modèles
mathématiques, ces outils de gestion qui conditionnent toutes les orientations
des grandes entreprises actuelles. La loi normale est un de ces outils.
Pour ce qui est de la pratique, nous laissons nos lecteurs, seuls responsables
devant leur classe, choisir de mélanger certaines parties de ce dossier avec
d'autres éléments relevant d'un tout autre point de vue. Nous leur suggérons de
parcourir l'exposé, fait par Michel Henry pour la régionale d'Aix Marseille de
l'APMEP,
dont nous vous proposons ci-dessous la conclusion :
Références : Aix Marseille Vert, Numéro 9 pages 3 à 18. Des lois
continues pourquoi et pour quoi faire ?
Disponible sur Internet à l'adresse :
http://www.apmep-aix-mrs.org/bulletin/index.htm.
« L'introduction
de lois continues en Terminale, outre la résolution de problèmes plus
intéressants que les problèmes traditionnels de combinatoire à propos de jeux
de hasard, a pour importance essentielle de rendre incontournable la notion de
modèle. La simulation informatique de situations simples y concourre aussi.
Le bénéfice qu'en tireront les élèves sera sans doute une compréhension plus
claire du statut du calcul des probabilités comme un outil mathématique des
plus performants pour maîtriser les problèmes concrets issus de la complexité
de la réalité, aussi bien dans les domaines des sciences de la nature que dans
les sciences économiques ou dans les sciences humaines. »