Série I

1°)Un cercle a un rayon de 175 cm .

Calculer sa longueur , l'exprimer en cm ( résultat arrondi à une décimale ) , puis en m ( arrondir à deux décimale prés).

2°) Un disque a un rayon de 52 mm. Calculer son aire , exprimer le résultat en cm² .

Série II

LE CERCLE : LONGUEUR ET CALCUL D’UNE DIMENSION

1) Les rayons d’une bicyclette mesurent 27 cm. Quel est le périmètre de chacune des roues ?

2) On veut entourer de grillage un puits circulaire de 1,15 m de rayon. Quelle longueur de grillage faudra-t-il acheter ?

3) Une roue de bicyclette a 55 cm de diamètre. Calculer son périmètre. Quelle distance aura été parcourue après 100 tours, puis 500 tours de roue ?

4) Un panneau de signalisation routière a 27,5 cm de rayon. Calculer son périmètre (en mètre).

5) On remplace le galon sur les deux cercles d’un abat-jour. Quelle sera la longueur de galon nécessaire si les diamètres des deux cercles sont respectivement de 30 cm et 35 cm ?

6) Calculer le périmètre du cercle ci-dessous.

7) Ma bicyclette a des roues de 700 mm de diamètre. Calculer la distance effectuée lorsqu’elles font trois tours.

8) Une fillette joue avec un cerceau de 80 cm de diamètre. Combien de tours complets le cerceau a-t-il effectué si elle l’a lancé sur une distance de 21 m ?

9) Sur une plaque de liège, François confectionne une cible pour jouer aux fléchettes. Avec du ruban adhésif de couleur, il veut représenter cinq cercle ayant pour rayon respectif : 4 cm, 8 cm, 12 cm, 16 cm et 20 cm. Il dispose de deux rubans adhésifs de 3 m chacun. Quelle longueur de ruban lui restera-t-il (au cm près) ?

10) Un arbre a une circonférence de 3,768 m. Calculer son diamètre.

11) Un disque 33 tours tourne 33 fois sur lui-même en une minute. Son diamètre étant de 30 cm, calculer la distance parcourue par un point quelconque du périmètre si la face dure 15 mn, puis 20 mn 45 s.

12) Sur le plafond d’une salle de spectacle, le décorateur a installé 4 rampes lumineuses circulaires, espacées les unes des autres de 1,40 m. La plus petite de ces rampes a un diamètre de 2 m. Si l’on branche une ampoule approximativement tous les 15 cm, combien d’ampoules, à l’unité près, composeront les rampes lumineuses ?

13) Le tronc d’un épicéa géant, âgé de 180 ans, a un pourtour de 3,30 m. Quel est, au cm près, le diamètre de ce tronc ?

14) Un cercle a un périmètre de 47,1 cm. Quel est son rayon ?

15) La Terre a 40 070,368 km de circonférence à l’équateur. Quel est, au km près, son diamètre ?

16) Un dresseur, placé au centre d’un manège circulaire, tient un cheval par une corde tendue et le fait tourner en suivant les barrières. Après 15 tours de piste, le cheval a parcouru 612,30 m. Quelle est la longueur de la corde ?

17) On entoure un bassin circulaire d’un grillage situé à 50 cm du bord. La longueur du grillage étant de 14,13 m, quel est le diamètre de ce bassin ?

Sport :

18 ) Problème « des tours de piste »: Calculs numériques

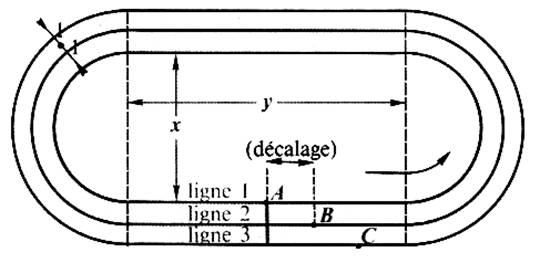
Une piste d'athlétisme possède 4 couloirs , un couloir par coureur.

Dans le dessin ci- dessus les couloirs ne sont pas dessinés ,les lignes représentent le milieu ( l'axe) de chaque couloir.

"x" = 60 m ; "y" = 100 m

1°) Calculer la longueur du tour de piste 1.

2°) Calculer la longueur du tour de piste 2.

3°) Calculer la longueur du tour de piste 3.

4°) Si l'on veut que le coureur "B" ligne 2 , parcourt la même distance que le coureur "A" ligne 1 , il faut un "décalage" entre les coureurs "A" et "B" (voir figure)

Calculer ce décalage .

5°) Montrer que le décalage entre les coureurs A et B et le même qu'entre les coureurs "B" et "C" .