GÉOMÉTRIE : SYNTHÈSE
1) L’écran de cinéma le plus
grand du monde est celui de l’Imaxe à Buenos Aires (Argentine). Il fait 30 m de long sur 23 m de
large. Que peut-on calculer ?
2) Un voilier est équipé de 2
voiles triangulaires : - première voile : b = 3 m ; H = 6,20
m ; - seconde voile : b = 4,30 m ; H = 6,40 m. Calculer la
surface totale de la voilure.
3) Le schéma ci-dessous
représente 2 poulies dont les axes sont distants de 72 cm. Le diamètre des
poulies est de 9 cm. Calculer, au cm par excès, la longueur de la courroie qui
les relie.
|
|
4) On entoure un jardin ayant
la forme d’un triangle régulier (équilatéral) avec une clôture valant 45,75 €
le m. Un côté du jardin mesure 39 m. Quel est le prix total de la
clôture ?
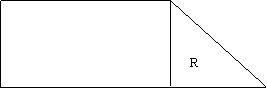
5) La grande surface ci-dessous
a la forme d’un trapèze dont les bases mesurent 200 m et 125 m pour une hauteur
de 75 m. Une partie du magasin, en forme de triangle rectangle, est utilisée
comme réserve. Calculer l’aire totale de la grande surface. Calculer l’aire de
la réserve. Calculer, de deux façons différentes, la superficie réservée à la
vente.
6) On veut carreler une pièce
rectangulaire de 13,50 m de longueur et 6,30 m de largeur avec du carrelage
revenant à 115 € le m². La main-d’œuvre coûtant 3 780 €, calculer la dépense
totale.
7) Un delphinarium circulaire
de 6 m de rayon est entouré d’un grillage. Calculer la longueur de celui-ci.
Calculer l’aire du bassin. Quatre dauphins évoluent dans le delphinarium. De
quelle superficie dispose chaque dauphin ?
8) A l’intérieur d’une porte
rectangulaire de 2 m de hauteur et 82 cm de largeur, papa pose une baguette
distante de 15 cm des bords de la porte. Quelle sera la longueur de baguette
nécessaire ? (Faire un croquis).
9) Un agriculteur veut
clôturer deux champs : l’un carré de 135 m de côté, l’autre rectangulaire
de 180 m de largeur et dont l’aire est le double de celle du terrain carré.
Calculer les périmètres de ces deux champs. L’agriculteur les entoure de 5
rangées de fil de fer barbelé, vendu en rouleaux de 75 m valant chacun 73,50 €.
Quelle sera la dépense ? (On ne tiendra pas compte des entrées).
10)
Un terrain rectangulaire a 60 m de longueur et son périmètre est la
moitié de celui d’un terrain carré de 84 m de côté. Quelle est la largeur du
terrain rectangulaire ?
11)
Une commune possédait un terrain rectangulaire de 100 m de longueur sur
45 m de largeur. Elle fait construire une route large de 10 m dans le sens de
la largeur du terrain, de façon à obtenir 2 parcelles carrées identiques. Faire
le croquis. Calculer l’aire d’une parcelle. Chaque parcelle est divisée en lots
de 506,25 m² vendus 1700 €. Combien la vente des lots rapportera-t-elle à la
commune ?
12)
Un parc a la forme ci-dessous. Sur l’aire totale, 1 850 m² sont réservés
aux allées, le reste étant ensemencé en pelouse. On prévoit, à cet effet, 3 kg
de graines à l’are. Combien coûtera l’engazonnement si le kg de graines vaut 15
€ ?

13)
Deux frères héritent de 150 000 €, d’un terrain rectangulaire (L = 23 m, l
= 17 m) et d’un terrain triangulaire (b = 22 m, H = 15 m). Ils vendent les
terrains à raison de 1 800 € l’are. Quelle sera, en €, la part d’héritage de
chacun des deux frères ?
14)
Dans le jardin rectangulaire de la mairie (L = 35 m, l = 23 m), les
jardiniers ont planté des fleurs sur deux massifs circulaires de 4,5 m de
rayon, bordés chacun d’un muret de pierres. Calculer la longueur d’un muret.
Autour des massifs, le jardin est ensemencé en pelouse. Calculer l’aire de
cette pelouse.
15)
Deux terrains ont le même périmètre ; l’un est carré, l’autre est
rectangulaire (L = 35 m, l = 25 m). Calculer la différence de leurs aires.
16)
Maman veut acheter du tissu afin de faire une nappe pour la table ronde
(Ø = 1,20 m) de la salle à manger. Elle souhaite que la nappe dépasse le bord
de la table de 20 cm. Quelle sera l’aire de tissu nécessaire à la confection de
la nappe (arrondir au dm²) ? Le tissu est vendu en coupon de 2 m de large.
Quelle quantité de tissu maman devra-t-elle acheter ? Quelle sera la perte
de tissu ? Si maman brode une dentelle sur le bord de la nappe, quelle en
sera la longueur (au cm près par excès) ?
17)
145 m
Monsieur Samsoon possédait un terrain carré de 145 m de côté. Pour
l’agrandir, il achète une parcelle rectangulaire longeant l’un des côtés de son
terrain (voir schéma). La longueur de sa nouvelle propriété est maintenant de
174 m. Calculer le périmètre et l’aire de son ancien terrain. Calculer les
dimensions de la parcelle achetée. Calculer le périmètre et l’aire de son
nouveau terrain. Quelle aire pourra-t-on encore calculer (il y a deux
solutions) ?

![]()
18)
La cuve d’une station-service (L = 5 m, l = 2 m, H = 2 m) n’est qu’à
moitié pleine. Calculer ce que rapportera la vente de l’essence qu’elle
contient si : - l’essence est vendue 1,77 € le litre ; - on garde 300
l au fond de la cuve par mesure de sécurité.
19)
Pour refaire le revêtement de la cour en forme de trapèze d’une école
(B : 25 m, b : 15 m, H : 14,5 m), on utilise du bitume valant
145,80 € le m². Trois ouvriers
travaillent 8 h/jour pendant une semaine (5 jours) à raison de 18,80 € de
l’heure. Quel est le coût de réfection de la cour ?
20)
25
m
Monsieur
Vladimir possédait un champ carré. Il achète un terrain voisin, d’une aire de 1
875 m² et d’une largeur de 25 m. (Voir schéma). Calculer le périmètre du champ
obtenu.

1) Une piscine (L : 25 m,
l : 14 m, P : 1,80 m) est totalement remplie. Calculer le volume
d’eau qu’elle contient. Combien de temps a pris son remplissage avec cinq
pompes débitant 70 hl à l’heure chacune ?
2) Une péniche a une soute
parallélépipédique de dimensions L : 40 m, l : 8 m, H : 3,80 m.
Calculer son volume en m3. Elle est remplie à moitié de sable. Pour
la vider, on utilise des bennes cubiques de 4 m d’arête. Combien de bennes faudra-t-il ?
Pour la construction d’une nouvelle route, on étale ensuite ce sable d’une
épaisseur de 0,20 m. Quelle superficie de route sera alors prête à
bitumer ? Si la route est large de 8 m, quelle longueur aura-t-on
couverte ?
