Corrigé : Périmètre et AIRES DE
SURFACES DÉCOMPOSABLES
Consignes :
A) Faire les
calculs de périmètre ; rédiger ( voir méthode )
B) Calculer les
aires des surfaces suivantes..
Sur
l’enseigne lumineuse d’un magasin, on voit la lettre ci-dessous. Calculer son
son aire en m.
0,20 m

Périmètre : 3,2m
Aire
= (0,90 x 0,20) + ( 0,5 x 0,2) = 0,28 m²
1)
Observer la figure
ci-dessous, calculer le périmètre , puis calculer l’aire de A, l’aire de B et
l’aire de C. Vérifier que les trois aires additionnées correspondent à l’aire
de la figure initiale.

Périmètre :
55 + 23 + 73
+ 15 = 166 m ;
« 23 » calcul avec
Pythagore ( racine carrée de 15 ² + 18²
)
Aire = ( 73 x
15) - (18 x 15 ) : 2 = 960 m² ; 1095 – 135
= 960 m²
3) Quelle est l’aire du terrain
de sport ci-dessous ? (Arrondir à 0,01 près).
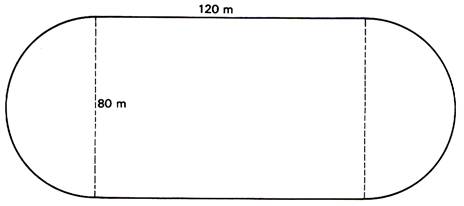
P
= 491,2 m
P = 120 x 2
+ 3,14 x2 x 40 = 240 + 251 ,2
A = 14 624 m²
A ) 120 x
80 +
3,14 x 40 x 40 = 9600 +
5 024 = 14 624 m²
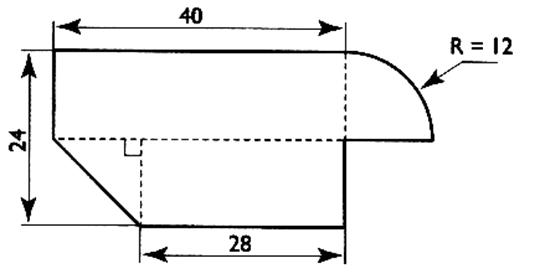
7°)La figure ci - dessous
représente une plaque de contreplaquée ( dimension en cm).
Calculer le périmètre de cette plaque .
Et son aire.
|
|
Conseils
: On peut décomposer cette plaque en
trois figures élémentaires ( 3 polygones ) est
un quart de disque . Quelle est la nature de chaque polygone ? Calculer l'aire de chacun
d'eux , celle du quart de disque , puis additionner pour obtenir l'aire de
l'ensemble.
Périmètre : = 40 +
(2x3,14x 12) / 4 + 12 + 12 + 28 +
![]() +12
+12
= 40 + 6 x
3,14 + 64 + ![]()
= 58,84
+ 64 + 16,97 = 139,97 m
Surafce : = ( 40x12)
+ ( (40+28) 12) /2 + ( 12²
x3,14)/ 4
= 480 + 408
+ 113,04
A =
1004,08 m²