|
Module : Géométrie .
|
DOSSIER : 90
- 91
|
|
LOGICIEL warmaths ; Pour Aide et
Formation Individualisée
; REMEDIATION mise à /NIVEAU : niveau VI
|
|
Info conseils et consignes.
|
TRAVAUX FORMATIFS :
niveau 6 et 5
.
Matière : MATHEMATIQUES.
|
Pré
requis :
dos 47
dos :58
|
|
LES TRIANGLES
et la MESURE DES ANGLES
|
|
INFO
COURS :
|
Info cours@ les triangles.
Info
@ cours « la mesure des angles »
|
|
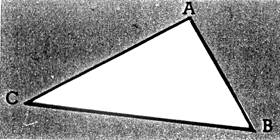
Un triangle est
une figure géométrique . Il est limité par 3 côtés qui joignent 3 points non
alignés.
Il
a : 3 côtés ; 3 sommets ; 3 angles ( tri- angle).
|
|
|
TRAVAUX
CONTROLE
|
|
Doc WR et wrdoc
|
|
Les
questions relatives à « ce qu’il faut retenir » , au « savoir » se reporter aux cours
.
|
|
TRAVAUX : EVALUATION
|
|
|
|
|
1. Nommez les côtés, les sommets, les angles
du triangle ABC ci-dessus.
|
|
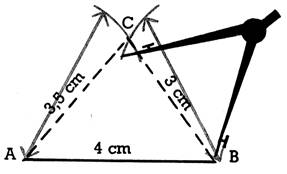
2.Tracez, selon le modèle
ci-contre, un triangle dont les côtés mesurent AB, 4 cm; BC, 3 cm; AC, 3,5
cm.
a) Tracez le segment AB (4 cm).
b) A l’aide du compas, déterminez C à 3 cm de
B, à 3,5 cm de A.
c) Joignez AC et BC par des droites.
|
|
|
3. 3 - Construisez de la
même façon deux triangles dont les côtés mesurent
a) 7cm;
6cm; 5cm;
b) 5cm; 4cm; 8cm.
Lequel de ces triangles a-t-il
un angle obtus ?
|
|
|
Des
lignes remarquables.
|
|
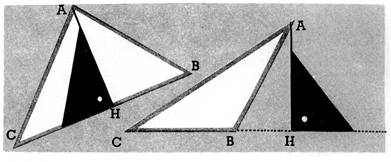
Hauteur. La droite AH part d’un sommet (A) et elle est
perpendiculaire au côté opposé (BC) ou à son prolongement on l’appelle hauteur
du triangle; le côté BC s’appelle alors base du triangle.
|
|
|
4.
a) Dessinez un triangle dont les côtés mesurent 8 cm, 9 cm et 10 cm.
b) A l’aide
de l’équerre, tracez ses 3 hauteurs (par chaque sommet ). Si votre dessin est
bien fait, les hauteurs se coupent au même point.
5. a) Dessinez un triangle dont un des angles est obtus.
b) A
l’aide de l’équerre, tracez ses 3 hauteurs deux d’entre elles tombent sur le
prolongement du côté opposé au sommet d’où elles partent. Prolongez ces
hauteurs si le dessin est bien fait, elles se coupent au même point, hors du
triangle.
Médianes elles joignent chaque
sommet au milieu du côté opposé.
6. Dessinez un triangle; marquez le milieu des côtés, puis tracez
les trois médianes. Si le dessin est bien fait, elles se coupent au même
point.
Bissectrices des angles.
7. Dessinez un triangle; découpez-le. Par pliage, marquez la
bissectrice de chaque angle. Si le pliage est bien fait, les bissectrices se
coupent au même point.
Autres lignes.
8. Dessinez
un triangle; découpez-le. Marquez les milieux des côtés, et joignez-les par
des segments. Découpez les triangles ainsi formés; superposez-les que remarquez-vous
? Coloriez-les diversement, puis refaites le grand triangle en les assemblant
dans un ordre différent.

|
|
LES MESURES DES ANGLES.
|
|
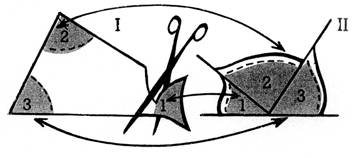
9. Dessinez et découpez un triangle;
découpez ses angles et assemblez-les comme l’indique la figure ci contre : à eux trois, ils forment un
angle plat (2 droits) ; vérifiez à
l’aide de l’équerre.
|
|
|
Retenons la somme des angles d’un triangle vaut 2 droits.
|
|
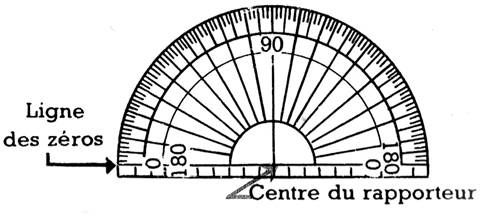
10. Examinez un rapporteur; il est gradué
de 0 à 180.
Chaque
graduation correspond à un angle de
« 1° » qui aurait son sommet au
centre
du rapporteur.
1
angle droit vaut 90° l’angle ; plat formé par la ligne des zéros vaut
l80°.
|
|
|
|
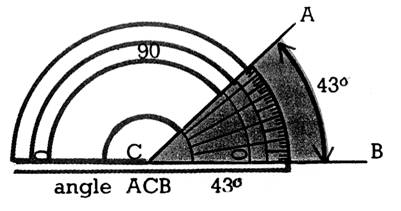
11. Dessinez
un triangle; mesurez ses angles à l’aide du rapporteur, en plaçant le centre du
rapporteur au sommet de l’angle, et la ligne des zéros sur un côté de
l’angle.
|
|
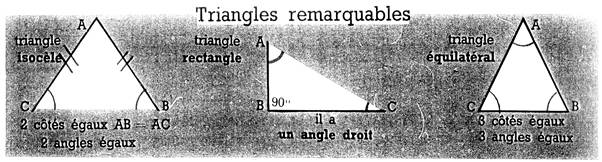
Les TRIANGLES
REMARQUABLES .
|
|
|
|
12. Puisque les 3 angles d’un triangle
valent ensemble 180° , combien chaque angle vaut-il de degrés dans le
triangle équilatéral?
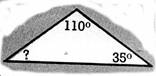
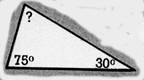
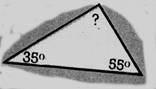
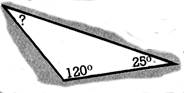
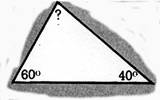
13. Calculs
|
|
Calculez la valeur du 3ème angle, dans les triangles ci-joint .
|
|
|
|
|
|
|
|
|
|
14 Assemblages. Dessinez, puis
découpez et assemblez des triangles équilatéraux égaux, de 2 cm de côté
|
|
a)

|
b)

|
|
c)

|
d)

|
|
e)

|
f)

|
g)

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|