|
Module : Géométrie . |
DOSSIER : 124 - 125 |
||||||||||
|
Warmaths ; Pour Aide et
Formation Individualisée
; REMEDIATION mise à /NIVEAU : niveau VI |
|||||||||||
|
TRAVAUX NORMATIFS PRIMAIRE / COLLEGE / LYCEE
Matière : MATHEMATIQUES. Niveau VI |
. ?? |
||||||||||
|
Corrigé :
LE CERCLE - LE PERIMETRE du CERCLE |
|||||||||||
|
Les questions
relatives à « ce qu’il faut retenir » , au « savoir » se reporter aux cours
. Info 1 @ cours
le cercle.
; Info 2 @ cours le périmètre cercle
; Info
2 @ cours niveau V le cercle. .
|
|||||||||||
|
INFO COURS : ; info :niveau
V @ |
|||||||||||
|
LE
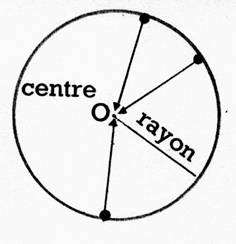
CERCLE . Tous les points du pourtour (on dit parfois la circonférence)
d’un cercle, sont à égale distance d’un point qui est le centre du cercle. La distance du centre au pourtour est le rayon du cercle. On trace des
cercles à l’aide d’un compas dont les pointes ont pour écartement la longueur
du rayon. |
|||||||||||
|
Le cercle Le cercle est une ligne courbe . |
Le disque Le disque est une surface !!! (voir dos 130 - 131) |
||||||||||
|
|
|
||||||||||
|
TRAVAUX : EVALUATION |
|||||||||||
|
1.Tracez
un cercle de 3 cm de rayon. Marquez plusieurs fois le rayon par des traits
fins, mesurez ces traits sont-ils bien tous égaux ? |
|||||||||||
|
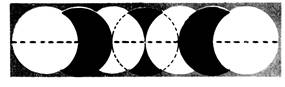
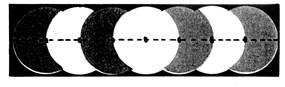
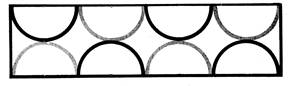
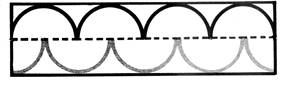
2 - A
l’aide d’un compas, et sans changer de rayon, faites les dessins ci-dessous,
en regardant bien où vous placez les
centres des cercles. |
|||||||||||
|
« A »
|
« B »
|
||||||||||
|
« C »
|
« D »
|
||||||||||
|
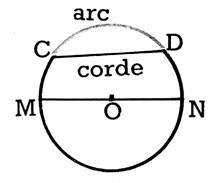
INFO cours :Un segment de droite (comme CD)
qui joint deux points du pourtour s’appelle « corde ». Une portion du pourtour s ‘appelle
« arc ». On dit que la corde CD sous-tend l’arc CD. Une corde qui passe
par le centre s ‘appelle « diamètre du cercle » ; le diamètre mesure deux fois la longueur du
rayon. |
|
||||||||||
|
3 Dessinez et découpez un cercle. Pliez-le
plusieurs fois en deux, afin de marquer des diamètres se coupent-ils bien
tous au centre ? Sont-ils bien tous égaux entre eux ? Comment, sans mesurer, voir
qu’ils mesurent chacun deux fois la longueur du rayon ? |
|||||||||||
|
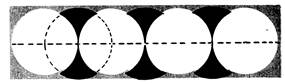
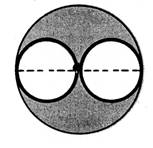
En repérant diamètres, centres, rayons, faites les dessins ci-dessous. |
|||||||||||
|
« A »
|
« B »
|
||||||||||
|
« C »
|
« D »
|
||||||||||
|
|
|||||||||||
|
« E »
|
« F »
|
||||||||||
|
|
|||||||||||
|
INFO COURS :
LE PERIMETRE |
|||||||||||
|
Le périmètre du
cercle (son tour) augmente selon le diamètre. |
|||||||||||
|
|
|||||||||||
|
1° . Découpez
dans une vieille carte postale trois cercles inégaux, ayant pour diamètre un
nombre entier de centimètres. En repérant un point du pourtour, faites-lui
faire un tour entier sur une ligne droite; mesurez la distance parcourue,
divisez-la par le diamètre;si VOUS avez bien opéré, vous trouvez
toujours le même quotient 3,14. Le quotient du périmètre d’un cercle par son
diamètre a une valeur fixe, qui n’est
pas exacte; on désigne cette valeur approchée par la lettre grecque ~r
(pi) c’est 3,14.. Apprendre : Périmètre
du cercle = Diamètre ´
3,14 Diamètre du
cercle = Périmètre : 3,14 |
|||||||||||
|
2.
Dites le périmètre d’un cercle dont le diamètre mesure : 10
cm; 4
m; 0,80 m 3. Dites le périmètre d’un cercle dont le rayon mesure :
1m;
12 m; 2,5
m 4. Dites le diamètre d’un cercle dont le
périmètre mesure :
3,14 m; 15,70 m; 2,355 m 5. Copiez
et complétez le tableau suivant |
|||||||||||
|
Rayon |
8 cm |
35 cm |
0,6 m |
0,3 m |
0,9 m |
||||||
|
Diamètre |
16 cm |
70 cm |
1,2 m |
0,6 m |
1,8 m |
||||||
|
Périmètre |
50,24 |
219,8 cm |
3,768 m |
1,884 m |
5, 652 m |
||||||
|
6. A l’aide
d’une ficelle, mesurez le périmètre de 3 arbres, à 1 m du sol. Calculez leur
diamètre. |
|||||||||||
|
7. Mesurez
le diamètre d’une roue : de bicyclette; de scooter; d’automobile. Calculez
son développement (longueur parcourue pour un tour de roue). |
|||||||||||
|
8.
Un tuyau de poêle a 12 cm de diamètre, et les bords de la tôle qu’on emploie
pour le fabriquer se recouvrent de 1 cm. Quelle largeur de tôle faut-il
courber pour obtenir ce tuyau? 37,68 + 1
= 38,68 cm
|
|||||||||||
|
9. # # Les 2
poulies ci-contre, de 40 cm de rayon, doivent
être réunies par une courroie, a) Dessinez cette courroie autour des
poulies, b) Calculez sa longueur. c) La courroie se vend par mètres entiers.
En comptant 20 cm pour la couture, quelle longueur faut-il en acheter ? 2,512 + 2,4
+ 2,4 + 0, 20 = 7,512 m |
|||||||||||
|
10. # # Une table
circulaire de 1,20 m de diamètre peut recevoir jusqu’à 3 rallonges. Deux
rallonges forment un carré. Dites le périmètre de la table: a) Sans rallonges;
b) avec 1, puis 2, puis 3 rallonges, c) En comptant 60 cm par convive,
combien de convives peuvent-ils prendre place autour de la table lorsqu’elle
a ses trois rallonges ?
|
|||||||||||