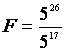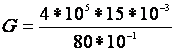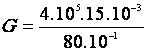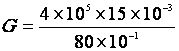Mathématiques : (donné à Wassigny 02)

Devoir commun n° ……….. ?  :

PARTIE NUMERIQUE ( 10 points)		Autres écritures : (écritures équivalentes)
Exercice n°1 ( 6 points)
	1) On pose  ;  ; Ecrire le nombre C sous la forme d’une fraction irréductible.	Opérations avec les fractions
	2°) On pose  ;  ; Ecrire sous la forme d’une puissance d’un nombre entier chacun des nombres D , E et F.	ou
	3°) Donner l’écriture décimale de « G » , puis son écriture scientifique.	ou
	4°) On donne Ecrire « H » sous la forme «  »	Autre écriture :
Exercice 2 ( 4 points)
	On donne E = ( 2x – 3 ) ² + ( 2x – 3) ( x + 8)
	1°) Développer et réduire l’expression algébrique E. 2°) Factoriser l’expression algébrique « E ». 3°) Calculer l’expression »E » quand «  x =  »

PARTIE GEOMETRIQUE		10 points
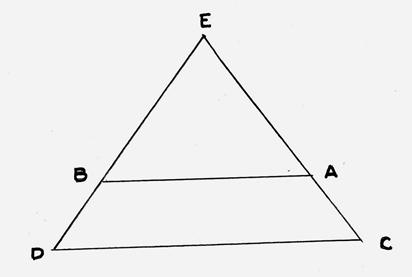
Exercice 1 ( 5 points)	La figure ci-dessous n’est pas en vraie grandeur ; l’unité est le centimètre (cm) Le point « B » appartient au « segment DE » , noté ( [DE] ) Le point « A » appartient au « segment CE » , noté ( [CE] )
	On donne : ED = 9 ; EB= 5,4 ; EA = 7,2 ; EC = 12
	Questions :
	1°) Montrer que la droite (AB) et (CD) sont parallèles.	Les rapports proportionnels
	2°) Calculer la longueur du segment [AB]
	3°) Montrer que les droites ( CE) et ( DE) sont perpendiculaires.	« réciproque de Pythagore »
	4°) Calculer la valeur arrondie au degré près de l’angle
		« les rapports trigonométriques »
Exercice n°2
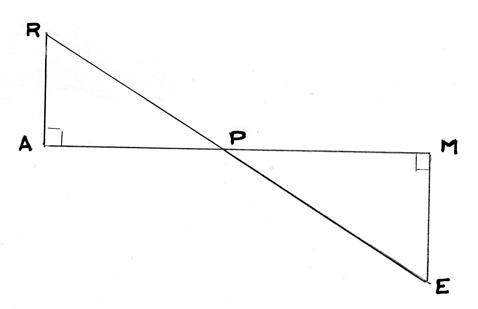
	La figure ci-dessous n’est pas en vraie grandeur ; Les points R , P et E sont alignés ainsi que les points A , P et M. 1°) « PAR » est un triangle rectangle en A ( on devrait dire : RPA ) On donne « AR= 2 cm » et « RP= 4 cm) Calculer « AP » et l’exprimer sous la forme «  » , où « a » et « b » sont des entiers.	=
	2°) Déterminer la mesure de l’angle « RPA »
	3°) Expliquer pourquoi les angles « RPA » et « MPE » ont la même mesure.
	4°) « PME » est un triangle rectangle en « M » . On donne « ME »= 3 cm . Calculer « PM » à 1 mm prés