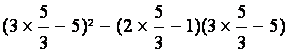Mathématiques :
(donné à Wassigny 02)
Le 30/11/2010
|
|
9 exercices : |
|
|
|
Leçon : (Développer ; réduire . et……leçon :factoriser ; et leçon sur « les identités remarquables » |
|
|
|
Exercice n° 1 : |
|
|
|
On
donne E = ( x + 3 ) ( 2 x – 3 ) – ( 2 x - 3 )² 1°)
Développer et réduire « E » 2°) Factoriser « E » . |
|
|
|
·
Remarque
E est de la forme : E =
A -
B Avec A
= ( x + 3 ) (
2 x – 3 ) et B =
( 2 x - 3 )² |
|
|
|
·
Développer A : ( x + 3 ) (
2 x – 3 ) = 2 x² - 3 x + 6x – 9 soit
A = 2
x² + 3 x - 9 |
|
|
|
·
Développer B : (
2 x - 3 )² ; de la forme ( a – b ) ² = a² - ab + b² ; avec « a » =
« 2x » et « b » =
3 ; B = (2x)² - 2 ( 2x ) ( 3) + ( 3 )² B = 4
x² - 12 x + 9 |
|
|
|
Remarque : l’expression 2 x – 3 peut s’écrire sous la forme de la somme algébrique : ( +2 x ) + (– 3) dont (2 x – 3)² peut s’écrire (avec des crochets) [ ( +2 x ) + (– 3) ] ² ou (avec des double parenthèses) (2 x – 3)² = ( ( +2 x ) + (– 3) ) ² |
|
|
|
Question : est ce que ( 2 x - 3 )² = ( (+2x) + (-3) ) ² ? |
|
|
|
( (+2x) + (-3) ) ² = (+2x)²
+ 2 (+2x) (-3) + (-3)² =
(+4 x² ) + 2 ( - 6x) + (
+9) =
(+4 x² ) + ( - 12 x) + (
+9) =
si l’on simplifie = 4 x² - 12 x + 9 |
|
|
|
Le développement de ( 2 x - 3 )² est-il égal au développement de ( (+2x) + (-3) ) ² Oui si dans ( 2 x - 3 )² « a » = 2x et « b » = 3 et si dans ( (+2x) + (-3) ) ² « a » = (+2x) et « b » = ( -3) |
|
|
|
A
= 2 x² + 3 x – 9 et
B = 4 x²
- 12 x + 9 E = A – B
E = ( 2 x² + 3 x – 9 ) – (4 x² - 12 x
+ 9 ) E = ( 2 x² +
3 x – 9 ) – 4 x² + 12 x
- 9 E =
2 x² + 3 x – 9 – 4 x² + 12
x - 9
E =
- 2 x² + 15 x – 18 Vérification =
si x = 5 Avant développement : E = ( x + 3 ) ( 2 x – 3 ) –
( 2 x - 3 )² E = ( 5 + 3 ) ( 2fois
5 – 3 ) – ( 2 fois 5 - 3 )² E = 8 fois 7
- 49 E = 56 – 49 = 7 Aprés développement: Et E = - 2 x²
+ 15x – 18 -
50 + 75 – 18 =
7 7 = 7 ; |
|
|
|
2°)
Factoriser E E
= ( x + 3 ) ( 2 x – 3 ) – ( 2 x - 3 )² E est de la forme A – B Avec
A = ( x + 3 ) ( 2 x – 3 ) Et Avec
B = ( 2 x - 3 )² = qui s’écrit ( 2 x - 3 ) ( 2 x - 3
) On remarque qu’il y a un
facteur commun : ( 2 x - 3 ) De
l’énoncé : E = ( x + 3 ) ( 2 x – 3 ) – ( 2 x -
3 )² On
passe à l’énoncé : E
= ( x + 3 ) ( 2 x – 3 ) – ( 2 x - 3 ) ( 2 x - 3 ) Avec comme facteur
commun : ( 2 x - 3 ) E = ( 2 x - 3 ) [ ( x + 3 ) -
( 2 x - 3 )] E = ( 2 x - 3 ) [ x + 3
- 2 x + 3 )] Résultat : E = ( 2 x - 3 )
(- x + 6 ) |
|
|
|
Exercice n° 2 : |
|
|
|
On donne
D = ( 3x -1 )² - ( 3 x – 1 ) ( 2 x - 3 ) |
|
|
|
1°) Développer et réduire « D » |
|
|
|
D = ( 3x -1 )² - ( 3 x – 1 )
( 2 x - 3 ) ·
( 3x -1 )² = (
3x -1 ) ( 3x -1 ) = 9 x² - 6 x + 1 ·
( 3 x – 1 ) ( 2 x - 3 ) = 6 x²
- 9 x – 2 x + 3 = 6 x² - 11 x + 3 D = ( 3x -1 )² - ( 3 x
– 1 ) ( 2 x - 3 ) ·
D = 9 x²
- 6 x + 1 – 6 x² +11x – 3 ·
D = 3
x² + 5 x -2 |
|
|
|
2°) Calculer la valeur numérique de
« D » pour « x = - 0,1 » |
|
|
|
Soit :
D = 3 x² + 5 x -2 ·
D = 3
( - 0,1) ² + 5 ( - 0,1) -2 ·
D =
0,03 – 0,5 – 2 ·
D = -
2,47 |
|
|
|
3°) Factoriser « D » . |
|
|
|
D = ( 3x -1 )² - ( 3 x – 1 )
( 2 x - 3 ) D = (
3x -1 ) ( 3x -1 ) - ( 3 x – 1 )
( 2 x - 3 ) Facteur
commun : ( 3x -1 ) D = ( 3x -1 ) [ ( 3x -1
) – ( 2 x – 3 ) ] D = ( 3x -1 ) ( 3x
-1 –
2 x + 3 ) D = ( 3x -1 ) ( x + 2
) |
|
|
|
Exercice n° 3 : |
|
|
|
On
donne D = ( 3x
- 5 )² - ( 2 x – 1 ) ( 3 x - 5 ) |
|
|
|
1°) Développer et réduire « D » |
|
|
|
On donne D = ( 3x - 5 )² - ( 2 x – 1 ) ( 3 x - 5 ) Forme
de D = A - B A = ( 3x - 5 )² = ( 3x - 5 ) ( 3x - 5 ) = 9 x² - 15 x – 15 x + 25 |
|
|
|
On
développe : A = 9 x²
- 30x + 25 B = 6 x² - 10 x – 3 x + 5 = 6 x² - 13 x + 5 |
|
|
|
D = A
- B Alors : D
= 9 x² - 30x + 25 - (6
x² - 13 x + 5) D
= 9 x² - 30x + 25 - 6
x² + 13 x - 5 D = 3 x² - 17 x + 20 |
|
|
|
|
|
|
|
2°) Factoriser « D » . |
|
|
|
On donne D = ( 3x - 5
)² -
( 2 x – 1 ) ( 3 x - 5 ) Forme
de D = A - B A = ( 3x - 5 )² = ( 3x
- 5 ) ( 3x - 5 ) Facteur
commun à A et B : ( 3x - 5 ) |
|
|
|
On
donne D = ( 3x
- 5 )² - ( 2 x – 1 ) ( 3 x - 5 ) D = ( 3x - 5 ) [ ( 3x
- 5 ) - ( 2 x – 1 ) ] D = ( 3x - 5 ) [ 3x -
5 -
2 x + 1 ] ; on a supprimé les parenthèses dans
les crochets. D = ( 3x - 5 ) [ x –
4 ] ; |
|
|
|
Si on développe : ( 3x - 5 ) [ x – 4
] = 3 x² - 12x – 5x + 20 ; On trouve D = 3 x² - 17x + 20 ce qui correspond à la réponse trouvée en 1° |
|
|
|
3°)
Calculer la valeur numérique de « D » pour « x = |
|
|
|
D = 3 . ( D = D = D = D = D = 0 |
|
|
|
Autre
procédure de calculs : On
donne D = ( 3x
- 5 )² - ( 2 x – 1 ) ( 3 x - 5 ) D = D = D = D = D = 0 |
|
|
|
Exercice n° 4 : |
|
|
|
On donne
P = ( x - 2 )
( 2 x + 1 ) – ( 2 x + 1 )² |
|
|
|
1°)
Développer et réduire l’expression
« P » |
|
|
|
P est de la forme = A
- B A =
( x - 2 ) ( 2 x + 1 )
on développe : = 2 x² + x – 4 x – 2 = 2
x² –
3 x – 2 B =
( 2 x + 1 )² = ( 2 x + 1 ) ( 2
x + 1 ) = 4 x² + 2 x + 2 x + 1 = 4 x² + 4 x + 1 On
remplace : P
= 2 x²
– 3 x – 2 - [4 x² + 4 x + 1 ] P
= 2 x²
– 3 x – 2 - 4 x²
- 4 x - 1 P = - 2 x²
- 7 x
- 3 |
|
|
|
|
|
|
|
|
|
|
|
2°) Factoriser « P » . |
|
|
|
P est de la forme = A
- B A
= ( x - 2 ) ( 2 x
+ 1 ) ; B = ( 2 x + 1 )² B
= ( 2 x + 1
)² = ( 2 x + 1 ) ( 2 x + 1 ) Facteur
commun : (
2 x + 1 ) On P = ( 2 x + 1 ) [( x - 2 ) - ( 2 x + 1 )] P
= ( 2 x + 1 )
[ x - 2 - 2 x - 1 ] P
= ( 2 x + 1 )
[ -
x - 3 ] P
= ( 2 x + 1 )
( - x
- 3 ) |
|
|
|
Si on développe P = ( 2 x + 1 ) (
- x
- 3 ) on trouvera P =
- 2 x² -
7 x - 3 |
|
|
|
3°) pour « x
= |
|
|
|
On donne P = ( x - 2 ) ( 2 x + 1 ) – ( 2 x + 1 )² |
|
|
|
P = ( P = ( Calcul : |
|
|
|
|
|
|
|
Exercice n° 5 : |
|
|
|
On donne
A = ( 2x - 10 ) ( x +
4 ) – ( x + 4 )² |
|
|
|
1°) Développer et réduire l’expression « A » |
|
|
|
|
|
|
|
2°) Factoriser « A » . |
|
|
|
|
|
|
|
Exercice n° 6 : |
|
|
|
On donne
E = ( 3x - 2 )² + 6 (
3x -2 ) |
|
|
|
1°) Développer et réduire l’expression « E » |
|
|
|
2°) Factoriser « E » . |
|
|
|
|
|
|
|
3°) Calculer « E »
pour « x = |
|
|
|
Exercice n° 7 : |
|
|
|
On donne
D = ( x - 3 ) ² +
( x - 3
) ( 2x + 5) |
|
|
|
1°) Développer et réduire l’expression « D » |
|
|
|
2°) Factoriser « D » . |
|
|
|
|
|
|
|
3°) Calculer « D » pour « x = - 2 » |
|
|
|
Exercice n° 8 : |
|
|
|
On donne
E = x² - 4 - ( x
+2 ) ( 3x - 5) |
|
|
|
1°)
Développer l’expression
« E » |
|
|
|
|
|
|
|
2°)
Calculer « E » lorsque « x = |
|
|
|
|
|
|
|
3°)
Factoriser « x²-4 » . En déduire une
factorisation de « E » |
|
|
|
x²- 4 est le développement de ( x + 2 ) ( x – 2)
|
|
|
|
Exercice n° 9 : |
|
|
|
On donne
E = ( 2
x - 5 )² - ( 3x + 1 ) ² |
|
|
|
1°) Développer l’expression « E » |
|
|
|
|
|
|
|
2°)
Après avoir remarquer que « E » est du modèle « a²-b² »,
écrire « E » sous la forme d’un produit de 2 facteurs. |
|
|
|
|
|
|
|
3°)
Calculer « E » lorsque « x = - 1 » , puis lorsque « x= 10 - 2 » |
|
|
|
|
|